Hostname: page-component-586b7cd67f-2plfb Total loading time: 0 Render date: 2024-11-21T10:12:21.487Z Has data issue: false hasContentIssue false
  • English
  • Français

Inertial wave activity during spin-down in a rapidly rotating penny shaped cylinder

Published online by Cambridge University Press:  15 March 2021

L. Oruba Open the ORCID record for L. Oruba [Opens in a new window] ,
A.M. Soward Open the ORCID record for A.M. Soward [Opens in a new window]  and
E. Dormy Open the ORCID record for E. Dormy [Opens in a new window]
L. Oruba*
Affiliation:
Laboratoire Atmosphères Milieux Observations Spatiales (LATMOS/IPSL), Sorbonne Université, UVSQ, CNRS, Paris, France
A.M. Soward*
Affiliation:
School of Mathematics and Statistics, Newcastle University, Newcastle upon TyneNE1 7RU, UK
E. Dormy*
Affiliation:
Département de Mathématiques et Applications, UMR-8553, École Normale Supérieure, CNRS, PSL University, 75005Paris, France
*
†Email addresses for correspondence: ludivine.oruba@latmos.ipsl.fr, andrew.soward@ncl.ac.uk, emmanuel.dormy@ens.fr
†Email addresses for correspondence: ludivine.oruba@latmos.ipsl.fr, andrew.soward@ncl.ac.uk, emmanuel.dormy@ens.fr
†Email addresses for correspondence: ludivine.oruba@latmos.ipsl.fr, andrew.soward@ncl.ac.uk, emmanuel.dormy@ens.fr
Get access Rights & Permissions [Opens in a new window]

Abstract

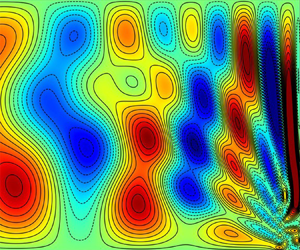
In an earlier paper, Oruba et al. (J. Fluid Mech., vol. 818, 2017, pp. 205–240) considered the primary quasi-steady geostrophic (QG) motion of a constant density fluid of viscosity $\nu$ that occurs during linear spin-down in a cylindrical container of radius $L$ and height $H$, rotating rapidly (angular velocity $\varOmega$) about its axis of symmetry subject to mixed rigid and stress-free boundary conditions for the case $L=H$. Direct numerical simulation (DNS) of the linear system at large $L= 10 H$ and Ekman number $E\leqslant \nu /H^2\varOmega =10^{-3}$ by Oruba et al. (J. Fluid Mech., vol. 888, 2020, p. 44) reveals significant inertial wave activity on the spin-down time scale. That analytic study, for $E\ll 1$, builds on the results of Greenspan & Howard (J. Fluid Mech., vol. 17, 1963, pp. 385–404) for an infinite plane layer $L\to \infty$. At large but finite distance from the symmetry axis, the meridional (QG-)flow, that causes the QG-spin-down, is blocked by the lateral boundary, which provides the primary QG-trigger for inertial wave generation. For the laterally unbounded layer, Greenspan and Howard identified, in addition to the QG-flow, inertial waves of maximum frequency (MF) $2\varOmega$, which are a manifestation of the transient Ekman layer. The blocking of these additional MF-waves by the lateral boundary provides an extra trigger that complements the QG-triggered inertial waves. Here we obtain analytic results for the full wave activity caused by the combined trigger ($\text {QG}+\text {MF}$) that faithfully capture their true character.

JFM classification

Geophysical and Geological Flows: Waves in rotating fluids
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 915 , 25 May 2021 , A53
Check for updates
Copyright
© The Author(s), 2021. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Abramowitz, M. & Stegun, I.A. 2010 NIST Handbook of Mathematical Functions (ed. F.W.J. Olver, D.W. Lozier, R.F. Boisvert & C.W. Clark). Cambridge University Press.Google Scholar
Atkinson, J.W., Davidson, P.A. & Perry, J.E.G. 2019 Dynamics of a trapped vortex in rotating convection. Phys. Rev. Fluids 4, 074701.CrossRefGoogle Scholar
Benton, E.R. & Clark, A. 1974 Spin-up. Annu. Rev. Fluid Mech. 6, 257–280.CrossRefGoogle Scholar
Cederlöf, U. 1988 Free-surface effects on spin-up. J. Fluid Mech. 187, 395–407.CrossRefGoogle Scholar
Chen, S., Lu, Y., Li, W. & Wen, Z. 2015 Identification and analysis of high-frequency oscillations in the eyewall of tropical cyclones. Adv. Atmos. Sci. 32, 624–634.CrossRefGoogle Scholar
Duck, P.W. & Foster, M.R. 2001 Spin-up of homogeneous and stratified fluids. Annu. Rev. Fluid Mech. 33, 231–263.CrossRefGoogle Scholar
Fischer, M.S., Rogers, R.F. & Reasor, P.D. 2020 The rapid intensification and eyewall replacement cycles of hurricane Irma (2017). Mon. Weath. Rev. 148, 981–1004.CrossRefGoogle Scholar
Greenspan, H.P. 1968 The Theory of Rotating Fluids. Cambridge University Press.Google Scholar
Greenspan, H.P. & Howard, L.N. 1963 On a time-dependent motion of a rotating fluid. J. Fluid Mech. 17, 385–404.CrossRefGoogle Scholar
Harlow, F.H. & Stein, L.R. 1974 Structural analysis of tornado-like vortices. J. Atmos. Sci. 31, 2081–2098.2.0.CO;2>CrossRefGoogle Scholar
Houze, R.A. Jr., Chen, S.S., Smull, B.F., Lee, W.-C. & Bell, M.M. 2007 Hurricane intensity and eyewall replacement. Science 315 (5816), 1235–1239.CrossRefGoogle ScholarPubMed
Kerswell, R.R. & Barenghi, C.F. 1995 On the viscous decay rates of inertial waves in a rotating circular cylinder. J. Fluid Mech. 285, 203–214.CrossRefGoogle Scholar
Klein, M., Seelig, T., Kurgansky, M.V., Ghasemi V., A., Borcia, I.D., Will, A., Schaller, E., Egbers, C. & Harlander, U. 2014 Inertial wave excitation and focusing in a liquid bounded by a frustum and a cylinder. J. Fluid Mech. 751, 255–297.CrossRefGoogle Scholar
Kurgansky, M.V., Seelig, T., Klein, M., Will, A. & Harlander, U. 2020 Mean flow generation due to longitudinal librations of sidewalls of a rotating annulus. Geophys. Astrophys. Fluid Dyn. 114 (6), 742–762.CrossRefGoogle Scholar
Montgomery, M.T., Snell, H.D. & Yang, Z. 2001 Axisymmetric spindown dynamics of hurricane-like vortices. J. Atmos. Sci. 58, 421–435.2.0.CO;2>CrossRefGoogle Scholar
Oruba, L., Davidson, P.A. & Dormy, E. 2018 Formation of eyes in large-scale cyclonic vortices. Phys. Rev. Fluids 3, 013502.CrossRefGoogle Scholar
Oruba, L., Soward, A.M. & Dormy, E. 2017 Spin-down in a rapidly rotating cylinder container with mixed rigid and stress-free boundary conditions. J. Fluid Mech. 818, 205–240.CrossRefGoogle Scholar
Oruba, L., Soward, A.M. & Dormy, E. 2020 On the inertial wave activity during spin-down in a rapidly rotating penny shaped cylinder: a reduced model. J. Fluid Mech. 888 (A9) 1–44.CrossRefGoogle Scholar
Read, P.L. 1986 a Super-rotation and diffusion of axial angular momentum. I. ‘Speed limits’ for axisymmetric flow in a rotating cylindrical fluid annulus. Q. J. R. Meteorol. Soc. 112, 231–251.Google Scholar
Read, P.L. 1986 b Super-rotation and diffusion of axial angular momentum. II. A review of quasiaxisymmetric models of planetary atmospheres. Q. J. R. Meteorol. Soc. 112, 253–272.CrossRefGoogle Scholar
Rotunno, R. 1979 A study in tornado-like vortex dynamics. J. Atmos. Sci. 36, 140–155.2.0.CO;2>CrossRefGoogle Scholar
Rotunno, R. 2014 Secondary circulations in rotating-flow boundary layers. Aust. Meteorol. Ocean. 64, 27–35.CrossRefGoogle Scholar
Rotunno, R. & Emanuel, K.A. 1987 An air-sea interaction theory for tropical cyclones. Part II: evolutionary study using a nonhydrostatic axisymmetric numerical model. J. Atmos. Sci. 44, 542–561.2.0.CO;2>CrossRefGoogle Scholar
Williams, G.P. 1968 Thermal convection in a rotating fluid annulus: part 3. Suppression of the frictional constraint on lateral boundaries. J. Atmos. Sci. 25, 1034–1045.2.0.CO;2>CrossRefGoogle Scholar
Yarom, E. & Sharon, E. 2014 Experimental observation of steady inertial wave turbulence in deep rotating flows. Nat. Phys. 10, 510–514.CrossRefGoogle Scholar
Zhang, K. & Liao, X. 2008 On the initial-value problem in a rotating circular cylinder. J. Fluid Mech. 610, 425–443.CrossRefGoogle Scholar
Zhang, K. & Liao, X. 2017 Theory and Modeling of Rotating Fluids: Convection, Inertial Waves and Precession. Cambridge University Press.CrossRefGoogle Scholar