Hostname: page-component-586b7cd67f-rcrh6 Total loading time: 0 Render date: 2024-11-24T17:27:38.006Z Has data issue: false hasContentIssue false
  • English
  • Français

The influence of a small upstream wire on transition in a rotating cylinder wake

Published online by Cambridge University Press:  25 March 2015

Anirudh Rao ,
Alexander Radi ,
Justin S. Leontini ,
Mark C. Thompson ,
John Sheridan  and
Kerry Hourigan
Anirudh Rao*
Affiliation:
Fluids Laboratory for Aeronautical and Industrial Research, FLAIR, Department of Mechanical and Aerospace Engineering, Monash University, Clayton, Victoria 3800, Australia
Alexander Radi
Affiliation:
Fluids Laboratory for Aeronautical and Industrial Research, FLAIR, Department of Mechanical and Aerospace Engineering, Monash University, Clayton, Victoria 3800, Australia
Justin S. Leontini
Affiliation:
Department of Mechanical and Product Design Engineering, Swinburne University of Technology, John St, Hawthorn 3122, Australia
Mark C. Thompson
Affiliation:
Fluids Laboratory for Aeronautical and Industrial Research, FLAIR, Department of Mechanical and Aerospace Engineering, Monash University, Clayton, Victoria 3800, Australia
John Sheridan
Affiliation:
Fluids Laboratory for Aeronautical and Industrial Research, FLAIR, Department of Mechanical and Aerospace Engineering, Monash University, Clayton, Victoria 3800, Australia
Kerry Hourigan
Affiliation:
Fluids Laboratory for Aeronautical and Industrial Research, FLAIR, Department of Mechanical and Aerospace Engineering, Monash University, Clayton, Victoria 3800, Australia
*
†Email address for correspondence: anirudh.rao@monash.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

Recent experimental research on rotating cylinder wakes has found that a previously numerically predicted subharmonic instability mode, mode C, occurs for considerably lower rotation rates than predicted through stability analysis, yet other mode transitions occur closer to the predicted onset. One difference between the theoretical and experimental set-ups is the use of a small-diameter hydrogen bubble visualisation wire placed upstream of the rotating cylinder. The current paper tests the hypothesis that a wire, of only 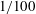$1/100$th of the cylinder diameter, placed five diameters upstream of the cylinder, sufficiently perturbs the flow to substantially affect certain wake transitions, including the onset of mode C. This is achieved using stability analysis of a flow that includes the upstream wire. The results indeed show that the wire of a tiny diameter induces a non-negligible asymmetry in the flow, triggering the subharmonic mode at substantially lower rotation rates. Furthermore, at higher rotation rates, the onset of two other three-dimensional modes are delayed to higher Reynolds numbers. These results make the point that even seemingly minute perturbations caused by minimally intrusive methods may result in substantially altered experimental flow behaviour.

JFM classification

Instability: Instability Instability: Parametric instability Wakes/Jets: Wakes
Type
Rapids
Information
Journal of Fluid Mechanics , Volume 769 , 25 April 2015 , R2
Copyright
© 2015 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Blackburn, H. M. & Sheard, G. J. 2010 On quasiperiodic and subharmonic Floquet wake instabilities. Phys. Fluids 22 (3), 031701.Google Scholar
Bottaro, A., Corbett, P. & Luchini, P. 2003 The effect of base flow variation on flow stability. J. Fluid Mech. 476, 293–302.Google Scholar
Brøns, M., Thompson, M. C. & Hourigan, K. 2009 Dye visualization near a 3d stagnation point: application to the vortex breakdown bubble. J. Fluid Mech. 622, 177–194.Google Scholar
Chomaz, J.-M. 2005 Global instabilities in spatially developing flows: non-normality and nonlinearity. Annu. Rev. Fluid Mech. 37, 357–392.Google Scholar
Gavarini, I., Bottaro, A. & Nieuwstadt, F. T. M. 2004 The initial stage of transition in pipe flow: role of optimal base-flow distortions. J. Fluid Mech. 517, 131–165.Google Scholar
Giannetti, F., Camarri, S. & Luchini, P. 2010 Structural sensitivity of the secondary instability in the wake of a circular cylinder. J. Fluid Mech. 651, 319–337.Google Scholar
Giannetti, F. & Luchini, P. 2007 Structural sensitivity of the first instability of the cylinder wake. J. Fluid Mech. 581, 167–197.Google Scholar
Hill, D. C.1992 A theoretical approach for analysing the restablisation of wakes. AIAA Paper 92-0067.Google Scholar
Lauga, E. & Bewley, T. R. 2004 Performance of a linear robust control strategy on a nonlinear model of spatially developing flows. J. Fluid Mech. 512, 343–374.Google Scholar
Leontini, J. S. & Thompson, M. C. 2013 Vortex-induced vibration of a diamond cross-section: sensitivity to corner shapes. J. Fluids Struct. 39, 371–390.Google Scholar
Luchini, P., Giannetti, F. & Pralits, J. O.2008 Structural sensitivity of linear and nonlinear global modes. In Proceedings of Fifth AIAA Theoretical Fluid Mechanics Conference, Seattle, Washington, AIAA Paper 2008-4227.Google Scholar
Luchini, P., Giannetti, F. & Pralits, J. O. 2009 Structural sensitivity of the finite-amplitude vortex shedding behind a circular cylinder. In IUTAM Symposium on Unsteady Separated Flows and their Control, vol. 14, pp. 151–160. Springer.CrossRefGoogle Scholar
Marquet, O., Sipp, D. & Jacquin, L. 2008a Sensitivity analysis and passive control of cylinder flow. J. Fluid Mech. 615, 221–252.Google Scholar
Marquet, O., Sipp, D., Jacquin, L. & Chomaz, J.-M.2008b Multiple scale and sensitivity analysis for the passive control of the cylinder flow. In Proceedings of Fifth AIAA Theoretical Fluid Mechanics Conference, 23–26 June 2008, Seattle, Washington, AIAA.Google Scholar
Pralits, J. O., Brandt, L. & Giannetti, F. 2010 Instability and sensitivity of the flow around a rotating circular cylinder. J. Fluid Mech. 650, 513–536.CrossRefGoogle Scholar
Radi, A., Thompson, M. C., Rao, A., Hourigan, K. & Sheridan, J. 2013 Experimental evidence of new three-dimensional modes in the wake of a rotating cylinder. J. Fluid Mech. 734, 567–594.Google Scholar
Rao, A., Leontini, J., Thompson, M. C. & Hourigan, K. 2013a Three-dimensionality in the wake of a rotating cylinder in a uniform flow. J. Fluid Mech. 717, 1–29.Google Scholar
Rao, A., Leontini, J. S., Thompson, M. C. & Hourigan, K. 2013b Three-dimensionality in the wake of a rapidly rotating cylinder in uniform flow. J. Fluid Mech. 730, 379–391.Google Scholar
Rao, A., Radi, A., Leontini, J. S., Thompson, M. C., Sheridan, J. & Hourigan, K. 2015 A review of rotating cylinder wake transitions. J. Fluids Struct. 53, 2–14.Google Scholar
Rao, A., Thompson, M. C., Leweke, T. & Hourigan, K. 2013c Dynamics and stability of the wake behind tandem cylinders sliding along a wall. J. Fluid Mech. 722, 291–316.Google Scholar
Ryan, K., Thompson, M. C. & Hourigan, K. 2005 Three-dimensional transition in the wake of elongated bluff bodies. J. Fluid Mech. 538, 1–29.Google Scholar
Sheard, G. J. 2011 Wake stability features behind a square cylinder: focus on small incidence angles. J. Fluids Struct. 27 (5–6), 734–742.Google Scholar
Sheard, G. J., Thompson, M. C. & Hourigan, K. 2005 Subharmonic mechanism of the mode C instability. Phys. Fluids 17 (11), 1–4.Google Scholar
Stewart, B. E., Thompson, M. C., Leweke, T. & Hourigan, K. 2010 The wake behind a cylinder rolling on a wall at varying rotation rates. J. Fluid Mech. 648, 225–256.Google Scholar
Strykowski, P. J. & Sreenivasan, K. R. 1990 On the formation and suppression of vortex ‘shedding’ at low Reynolds number. J. Fluid Mech. 218, 71–107.Google Scholar
Thompson, M. C. & Hourigan, K. 2003 The sensitivity of steady vortex breakdown bubbles in confined cylinder flows to rotating lid misalignment. J. Fluid Mech. 496, 129–138.Google Scholar
Thompson, M. C., Hourigan, K., Cheung, A. & Leweke, T. 2006 Hydrodynamics of a particle impact on a wall. Appl. Math. Model. 30, 1356–1369.CrossRefGoogle Scholar
Yildirim, I., Rindt, C. C. M. & van Steenhoven, A. A. 2013a Energy contents and vortex dynamics in Mode-C transition of wired-cylinder wake. Phys. Fluids 25 (5), 054103.Google Scholar
Yildirim, I., Rindt, C. C. M. & van Steenhoven, A. A. 2013b Mode C flow transition behind a circular cylinder with a near-wake wire disturbance. J. Fluid Mech. 727, 30–55.Google Scholar
Zhang, H.-Q., Fey, U., Noack, B. R., Konig, M. & Eckelemann, H. 1995 On the transition of the cylinder wake. Phys. Fluids 7 (4), 779–794.Google Scholar