Article contents
Influence of the velocity field on scalar transport in gaseous transverse jets
Published online by Cambridge University Press: 17 November 2017
Abstract
The present experiments explored the dynamical character of the gaseous jet injected flush into cross-flow for variable jet-to-cross-flow momentum flux ratios 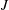 $J$ (5, 12 and 41) and density ratios
$J$ (5, 12 and 41) and density ratios 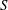 $S$ (0.35 and 1.0). Contoured nozzle and straight pipe injectors were studied here, with the jet Reynolds number fixed at 1900 as other flow parameters were varied. Simultaneous acetone planar laser-induced fluorescence (PLIF) imaging and stereo particle image velocimetry (PIV) were used to study the relationships between scalar and velocity/vorticity fields, with a special focus on comparing PLIF-based extraction of scalar dissipation rates and local strain rates with PIV-based local strain rates in the upstream and downstream shear layers of the jet. There was remarkable similarity between the scalar and vorticity fields for the jet in cross-flow, spanning conditions for absolutely unstable upstream jet shear layers at low
$S$ (0.35 and 1.0). Contoured nozzle and straight pipe injectors were studied here, with the jet Reynolds number fixed at 1900 as other flow parameters were varied. Simultaneous acetone planar laser-induced fluorescence (PLIF) imaging and stereo particle image velocimetry (PIV) were used to study the relationships between scalar and velocity/vorticity fields, with a special focus on comparing PLIF-based extraction of scalar dissipation rates and local strain rates with PIV-based local strain rates in the upstream and downstream shear layers of the jet. There was remarkable similarity between the scalar and vorticity fields for the jet in cross-flow, spanning conditions for absolutely unstable upstream jet shear layers at low 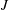 $J$ or
$J$ or  $S$ values to conditions for convectively unstable shear layers for larger
$S$ values to conditions for convectively unstable shear layers for larger 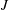 $J$ , equidensity conditions (Megerian et al., J. Fluid Mech., vol. 593, 2007, pp. 93–129; Getsinger et al., Exp. Fluids, vol. 53, 2012, pp. 783–801). Proper orthogonal decomposition applied to both scalar and velocity fields revealed strengthening instabilities in both the upstream shear layer and in the jet’s wake as
$J$ , equidensity conditions (Megerian et al., J. Fluid Mech., vol. 593, 2007, pp. 93–129; Getsinger et al., Exp. Fluids, vol. 53, 2012, pp. 783–801). Proper orthogonal decomposition applied to both scalar and velocity fields revealed strengthening instabilities in both the upstream shear layer and in the jet’s wake as 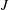 $J$ was reduced. The simultaneous measurements allowed PLIF-extracted scalar dissipation rates and strain rates to be determined via a flamelet-like model and compared with PIV-extracted strain rates, each in the diffusion layer-normal direction. There was generally very good qualitative and quantitative agreement for these metrics in both the jet upstream and downstream shear layers for most flow conditions, with excellent correspondence to locations of shear layer vorticity roll up, although downstream shear layer strain rates in some cases showed lesser correspondence between PLIF- and PIV-based data. Such differences are shown to potentially result from diffusion and resolution effects as well as the influence of three-dimensional and transient effects which can be more significant in the lee side of the jet. Nevertheless, the present results reveal interesting dynamics and demonstrate the importance of strain fields in enhanced diffusion and transport phenomena.
$J$ was reduced. The simultaneous measurements allowed PLIF-extracted scalar dissipation rates and strain rates to be determined via a flamelet-like model and compared with PIV-extracted strain rates, each in the diffusion layer-normal direction. There was generally very good qualitative and quantitative agreement for these metrics in both the jet upstream and downstream shear layers for most flow conditions, with excellent correspondence to locations of shear layer vorticity roll up, although downstream shear layer strain rates in some cases showed lesser correspondence between PLIF- and PIV-based data. Such differences are shown to potentially result from diffusion and resolution effects as well as the influence of three-dimensional and transient effects which can be more significant in the lee side of the jet. Nevertheless, the present results reveal interesting dynamics and demonstrate the importance of strain fields in enhanced diffusion and transport phenomena.
JFM classification
Information
- Type
- JFM Papers
- Information
- Copyright
- © 2017 Cambridge University Press
References
- 28
- Cited by


