Hostname: page-component-5cf477f64f-h6p2m Total loading time: 0 Render date: 2025-04-03T16:22:53.719Z Has data issue: false hasContentIssue false
  • English
  • Français

Influence of turbulent fluctuations on detonation propagation

Published online by Cambridge University Press:  05 April 2017

Brian McN. Maxwell Open the ORCID record for Brian McN. Maxwell [Opens in a new window] ,
R. R. Bhattacharjee ,
S. S. M. Lau-Chapdelaine ,
S. A. E. G. Falle ,
G. J. Sharpe  and
M. I. Radulescu
Brian McN. Maxwell*
Affiliation:
Department of Mechanical Engineering, University of Ottawa, 161 Louis Pasteur, Ottawa, K1N 6N5, Canada
R. R. Bhattacharjee
Affiliation:
Department of Mechanical Engineering, University of Ottawa, 161 Louis Pasteur, Ottawa, K1N 6N5, Canada
S. S. M. Lau-Chapdelaine
Affiliation:
Department of Mechanical Engineering, University of Ottawa, 161 Louis Pasteur, Ottawa, K1N 6N5, Canada
S. A. E. G. Falle
Affiliation:
School of Mathematics, University of Leeds, Leeds LS2 9JT, UK
G. J. Sharpe
Affiliation:
Blue Dog Scientific Ltd, 1 Mariner Court, Wakefield WF4 3FL, UK
M. I. Radulescu
Affiliation:
Department of Mechanical Engineering, University of Ottawa, 161 Louis Pasteur, Ottawa, K1N 6N5, Canada
*
†Email address for correspondence: bmaxwell@uottawa.ca
Get access Rights & Permissions [Opens in a new window]

Abstract

The present study addresses the reaction zone structure and burning mechanism of unstable detonations. Experiments investigated mainly two-dimensional methane–oxygen cellular detonations in a thin channel geometry. The sufficiently high temporal resolution permitted the determination of the probability density function of the shock distribution, a power law with an exponent of 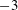$-3$, and the burning rate of unreacted pockets from their edges – through surface turbulent flames with a speed approximately 3–7 times larger than the laminar one at the local conditions. Numerical simulations were performed using a novel large-eddy simulation method where the reactions due to both autoignition and turbulent transport were treated exactly at the subgrid scale in a reaction–diffusion formulation. The model is an extension of Kerstein and Menon’s linear eddy model for large-eddy simulation to treat flows with shock waves and rapid gas-dynamic transients. The two-dimensional simulations recovered well the amplification of the laminar flame speed due to the turbulence generated mainly by the shear layers originating from the triple points and subsequent Richtmyer–Meshkov instability associated with the internal pressure waves. The simulations clarified how the level of turbulence generated controlled the burning rate of the pockets, the hydrodynamic thickness of the wave, the cellular structure and its distribution. Three-dimensional simulations were found to be in general good agreement with the two-dimensional ones, in that the subgrid-scale model captured the ensuing turbulent burning once the scales associated with the cellular dynamics, where turbulent kinetic energy is injected, are well resolved.

JFM classification

Compressible Flows: Compressible Flows Compressible Flows: Detonation waves Mixing: Turbulent mixing
Type
Papers
Information
Journal of Fluid Mechanics , Volume 818 , 10 May 2017 , pp. 646 - 696
Check for updates
Copyright
© 2017 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abdel-Gayed, R. G., Al-Khishali, K. J. & Bradley, D. 1984 Turbulent burning velocities and flame straining in explosions. Proc. R. Soc. Lond. A 391, 393–414.Google Scholar
Austin, J. M.2003 The role of instability in gaseous detonation. PhD thesis, California Institute of Technology, Pasadena, CA.Google Scholar
Batchelor, G. K. 1969 Computation of the energy spectrum in homogeneous two-dimensional turbulence. Phys. Fluids Suppl. II 12, 233–673.Google Scholar
Bhattacharjee, R. R.2013 Experimental investigation of detonation re-initiation mechanisms following a Mach reflection of a quenched detonation. Master’s thesis, University of Ottawa, Ottawa, Canada.Google Scholar
Borzou, B. & Radulescu, M. I. 2016 Dynamics of detonations with a constant mean flow divergence. J. Fluid Mech. (submitted); arXiv:1606.05323.Google Scholar
Bradley, D. 1992 How fast can we burn? In 24th Symp. (Intl) on Combustion, pp. 247–262. The Combustion Inst.Google Scholar
Browne, S., Liang, Z. & Shepherd, J. E. 2005 Detailed and Simplified Chemical Reaction Mechanisms for Detonation Simulation. Stanford University: Fall Technical Meeting Western States Section of the Combustion Institute.Google Scholar
Cael, G., Ng, H. D., Bates, K. R., Nikiforakis, N. & Short, M. 2009 Numerical simulation of detonation structures using a thermodynamically consistent and fully conservative reactive flow model for multi-component computations. Proc. R. Soc. Lond. A 465, 2135–2153.Google Scholar
Calhoon, W. H. & Menon, S. 1996 Subgrid modeling for reacting large eddy simulations. In AIAA 34th Aerospace Sciences Meeting and Exhibition.Google Scholar
Calhoon, W. H., Menon, S. & Goldin, G. 1995 Comparison of reduced and full chemical mechanisms for nonpremixed turbulent H2-air jet flames. Combust. Sci. Technol. 104, 115–141.Google Scholar
Cannon, S., Adumitroaie, V., McDaniel, K. & Smith, C.2001 LES software for the design of low emission combustion systems for vision 21 plants. CFDRC Rep. No. 8321/2. CFD Research Corporation.Google Scholar
Chakravarthy, V. K. & Menon, S. 2000 Subgrid modeling of turbulent premixed flames in the flamelet regime. Flow Turbul. Combust. 65, 133–161.Google Scholar
Chakravarthy, V. K. & Menon, S. 2001 Linear eddy simulations of Reynolds number and Schmidt number effects on turbulent scalar mixing. Phys. Fluids 13, 488–499.Google Scholar
Chasnov, J. R. 1991 Simulation of the Kolmogorov inertial subrange using an improved subgrid model. Phys. Fluids A 3, 188–200.Google Scholar
Combest, D. P., Ramachandran, P. A. & Dudukovic, M. P. 2011 On the gradient hypothesis and passive scalar transport in turbulent flows. Ind. Engng Chem. Res. 50, 8817–8823.Google Scholar
Danilov, S. D. & Gurarie, D. 2000 Quasi-two-dimensional turbulence. Phys.-Upsekhi 43 (9), 863–900.Google Scholar
Edwards, D. H. & Jones, A. T. 1978 The variation in strength of transverse shocks in detonation waves. J. Phys. D: Appl. Phys. 11, 155–166.Google Scholar
Falle, S. A. E. G. 1991 Self-similar jets. Mon. Not. R. Astron. Soc. 250, 581–596.CrossRefGoogle Scholar
Falle, S. A. E. G. & Giddings, J. R. 1993 Body capturing using adaptive cartesian grids. In Numerical Methods for Fluid Dynamics IV, pp. 337–343. Oxford University Press.Google Scholar
Fay, J. A. 1959 Two-dimensional gaseous detonations: velocity deficit. Phys. Fluids 2, 283–289.Google Scholar
Fickett, W. & Davis, W. C. 1979 Detonation Theory and Experiment. Dover.Google Scholar
Frisch, U. 2000 Turbulence: The Legacy of A. N. Kolmogorov. Cambridge University Press.Google Scholar
Gamezo, V. N., Desbordes, D. & Oran, E. S. 1999 Two-dimensional reactive flow dynamics in cellular detonation waves. Shock Waves 9, 11–17.Google Scholar
Gamezo, V. N., Vasil’ev, A. A., Khokhlov, A. M. & Oran, E. S. 2000 Fine cellular structures produced by marginal detonations. Proc. Combust. Inst. 28, 611–617.CrossRefGoogle Scholar
Goodwin, D. G., Moffat, H. K. & Speth, R. L.2016 Cantera: an object-oriented software toolkit for chemical kinetics, thermodynamics, and transport processes. http://www.cantera.org, version 2.2.1.Google Scholar
Gottiparthi, K. C., Genin, F., Srinivasan, S. & Menon, S. 2009 Simulation of cellular detonation structures in ethylene-oxygen mixtures. In 47th AIAA Aerospace Science Meeting and Exhibition.Google Scholar
Jozefik, Z., Kerstein, A. R. & Schmidt, H. 2016 Simulation of shock-turbulent deflagration and detonation regimes using one-dimensional turbulence. Combust. Flame 167, 53–67.Google Scholar
Kao, S. & Shepherd, J. E.2008 Numerical solution methods for control volume explosions and ZND detonation structure. GALCIT Rep. FM2006.007. California Institute of Technology: Aeronautics and Mechanical Engineering.Google Scholar
Kerstein, A. R. 1988 A linear-eddy model of turbulent scalar transport and mixing. Combust. Sci. Technol. 60, 391–421.Google Scholar
Kerstein, A. R. 1989 Linear-eddy modeling of turbulent transport. II: application to shear layer mixing. Combust. Flame 75, 397–413.Google Scholar
Kerstein, A. R. 1990 Linear-eddy modeling of turbulent transport. Part 3: mixing and differential molecular diffusion in round jets. J. Fluid Mech. 216, 411–435.Google Scholar
Kerstein, A. R. 1991a Linear-eddy modeling of turbulent transport. Part 6: microstructure of diffusive scalar mixing fields. J. Fluid Mech. 231, 361–394.CrossRefGoogle Scholar
Kerstein, A. R. 1991b Linear-eddy modeling of turbulent transport. Part V: geometry of scalar interfaces. Phys. Fluids A 3, 1110–1114.Google Scholar
Kerstein, A. R. 1992a Linear-eddy modeling of turbulent transport. Part 4: structure of diffusion flames. Combust. Sci. Technol. 81, 75–96.Google Scholar
Kerstein, A. R. 1992b Linear-eddy modeling of turbulent transport. Part 7: finite-rate chemistry and multi-stream mixing. J. Fluid Mech. 240, 289–313.CrossRefGoogle Scholar
Kiyanda, C. B. & Higgins, A. J. 2013 Photographic investigation into the mechanism of combustion in irregular detonation waves. Shock Waves 23, 115–130.Google Scholar
Kraichnan, R. H. 1967 Inertial ranges in two-dimensional turbulence. Phys. Fluids 10, 1417–1423.Google Scholar
Kraichnan, R. H. 1971 Inertial-range transfer in two- and three-dimensional turbulence. J. Fluid Mech. 47, 525–535.Google Scholar
Lau-Chapdelaine, S. S. M. & Radulescu, M. I. 2016 Viscous solution of the triple-shock reflection problem. Shock Waves 26, 551–560.Google Scholar
Lee, J. H. S. 1984 Dynamic parameters of gaseous detonations. Annu. Rev. Fluid Mech. 16, 311–336.Google Scholar
Lee, J. H. S. & Radulescu, M. I. 2005 On the hydrodynamic thickness of cellular detonations. Combust. Explos. Shock Waves 41 (6), 745–765.Google Scholar
Leith, C. E. 1968 Diffusion approximation for two-dimensional turbulence. Phys. Fluids 11, 671–673.Google Scholar
Leveque, R. J. 2002 Finite Volume Methods for Hyperbolic Problems. Cambridge University Press.Google Scholar
Lilly, D. K.1966 The representation of small-scale turbulence in numerical simulation experiments. NCAR Manuscript 281, National Center for Atmospheric Research.Google Scholar
Lundstrom, E. A. & Oppenheim, A. K. 1969 On the influence of non-steadiness on the thickness of the detonation wave. Proc. R. Soc. Lond. A 310, 463–478.Google Scholar
Mach, P. & Radulescu, M. I. 2011 Mach reflection bifurcations as a mechanism of cell multiplication in gaseous detonations. Proc. Combust. Inst. 33, 2279–2285.Google Scholar
Mahmoudi, Y., Karimi, N., Deiterding, R. & Emami, S. 2014 Hydrodynamic instabilities in gaseous detonations: comparison of Euler, Navier–Stokes, and large-eddy simulation. J. Propul. Power 30 (2), 384–396.Google Scholar
Massa, L., Austin, J. M. & Jackson, T. L. 2007 Triple-point shear layers in gaseous detonation waves. J. Fluid Mech. 586, 205–248.Google Scholar
Mathey, F. & Chollet, J. P. 1997 Subgrid-scale model of scalar mixing for large eddy simulations of turbulent flows. In Direct and Large-Eddy Simulation II (ed. Galperin, B. & Orszag, S. A.), pp. 103–114. Kluwer Academic.Google Scholar
Maxwell, B. M.2016 Turbulent combustion modelling of fast-flames and detonations using compressible LEM-LES. PhD thesis, Ottawa-Carleton Institute for Mechanical and Aerospace Engineering, University of Ottawa, Ottawa, Canada.Google Scholar
Maxwell, B. M., Falle, S. A. E. G., Sharpe, G. & Radulescu, M. I. 2015 A compressible-LEM turbulent combustion subgrid model for assessing gaseous explosion hazards. J. Loss Prev. Process. Ind. 36, 460–470.Google Scholar
McMurtry, P. A., Menon, S. & Kerstein, A. R. 1992 A linear eddy sub-grid model for turbulent reacting flows: application to hydrogen-air combustion. In 24th Symp. (Intl) on Combustion, pp. 271–278. The Combustion Inst.Google Scholar
Menon, S. & Calhoon, W. H. 1996 Subgrid mixing and molecular transport modeling in a reacting shear layer. In 26th Symp. (Intl) on Combustion, pp. 59–66. The Combustion Inst.Google Scholar
Menon, S. & Kerstein, A. R. 1992 Stochastic simulations of the structure and propagation rate of turbulent premixed flames. In 24th Symp. (Intl) on Combustion, pp. 443–450. The Combustion Inst.Google Scholar
Menon, S. & Kerstein, A. R. 2011 The linear-eddy model. In Turbulent Combustion Modeling: Advances, New Trends and Perspectives, chap. 10, pp. 221–247. Springer.Google Scholar
Menon, S., McMurtry, P. A., Kerstein, A. R. & Chen, J. Y. 1994 Prediction of NOx production in a turbulent hydrogen-air jet flame. J. Propul. Power 10 (2), 161–168.Google Scholar
Menon, S., Patrick, A., McMurtry, A. & Kerstein, A. R. 1993 A linear-eddy mixing model for large eddy simulation of turbulent combustion. In Large Eddy Simulation of Complex Engineering and Geophysical Flows, chap. 14, pp. 287–314. Cambridge University Press.Google Scholar
Mevel, R., Davidenko, D., Lafosse, F., Chaumeix, N., Dupre, G., Paillard, C.-E. & Shepherd, J. E. 2015 Detonation in hydrogen-nitrous oxide-diluent mixtures: an experimental and numerical study. Combust. Flame 162, 1638–1649.Google Scholar
Oran, E. S., Young, T. R., Boris, J. P. & Picone, J. M. 1982 A study of detonation structure: the formation of unreacted gas pockets. In 19th Symp. (Intl) on Combustion. The Combustion Inst.Google Scholar
Paolucci, S.1982 On the filtering of sound from the Navier–Stokes equations. Tech. Rep. Livermore, CA.Google Scholar
Pintgen, F., Eckett, C. A., Austin, J. M. & Shepherd, J. E. 2003 Direct observations of reaction zone structure in propagating detonations. Combust. Flame 133, 211–229.Google Scholar
Poinsot, T. & Veynante, D. 2005 Theoretical and Numerical Combustion, 2nd edn. Edwards.Google Scholar
Pope, S. 2000 Turbulent Flows. Cambridge University Press.Google Scholar
Pope, S. B. 2004 Ten questions concerning the large-eddy simulation of turbulent flows. New J. Phys. 6, 35.CrossRefGoogle Scholar
Porumbel, I.2006 Large eddy simulation of bluff body stabilized premixed and partially premixed combustion. PhD thesis, School of Aerospace Engineering, Georgia Institute of Technology, Atlanta, Georgia.Google Scholar
Radulescu, M. I., Sharpe, G. J., Law, C. K. & Lee, J. H. S. 2007 The hydrodynamic structure of unstable cellular detonations. J. Fluid Mech. 580, 31–81.Google Scholar
Radulescu, M. I., Sharpe, G. J., Lee, J. H. S., Kiyanda, C. B., Higgins, A. J. & Hanson, R. K. 2005 The ignition mechanism in irregular structure gaseous detonations. Proc. Combust. Inst. 30, 1859–1867.CrossRefGoogle Scholar
Richtmyer, R. D. & Morton, K. W. 1967 Difference Methods for Initial-Value Problems. Interscience Publishers.Google Scholar
Sankaran, V.2003 Sub-grid combustion modeling for compressible two-phase reacting flows. PhD thesis, School of Aerospace Engineering, Georgia Institute of Technology, Atlanta, Georgia.Google Scholar
Sankaran, V. & Menon, S. 2005 LES of scalar mixing in supersonic mixing layers. Proc. Combust. Inst. 30, 2835–2842.Google Scholar
Schumann, U. 1975 Subgrid scale model for finite difference simulations of turbulent flows in plane channels and annuli. J. Comput. Phys. 18, 376–404.Google Scholar
Settles, G. S. 2001 Schlieren and Shadowgraph Techniques. Springer.Google Scholar
Sharpe, G. J. 2001 Transverse waves in numerical simulations of cellular detonations. J. Fluid Mech. 447, 31–51.Google Scholar
Shepherd, J. E. 2009 Detonation in gases. Proc. Combust. Inst. 32, 83–98.Google Scholar
Smith, G. P., Golden, D. M., Frenklach, M., Moriarty, N. W., Eiteneer, B. E., Goldenberg, M., Bowman, C. T., Hanson, R. K., Song, S., Gardiner, W. C. et al. 2016 GRI-Mech 3.0. http://www.me.berkeley.edu/gri_mech/.Google Scholar
Smith, T. & Menon, S. 1996 Model simulations of freely propagating turbulent premixed flames. In 26th Symp. (Intl) on Combustion, pp. 299–306. The Combustion Inst.Google Scholar
Smith, T. & Menon, S. 1997 One-dimensional simulations of freely propagating turbulent premixed flames. Combust. Sci. Technol. 128, 99–130.Google Scholar
Strehlow, R. 1968 Gas phase detonations: recent developments. Combust. Flame 12, 81–101.Google Scholar
Subbotin, V. A. 1975 Collision of transverse detonation waves. Combust. Explosions Shock Waves 11 (3), 411–414.Google Scholar
Tannehill, J. C., Anderson, D. A. & Pletcher, R. H. 1997 Computational Fluid Mechanics and Heat Transfer, 2nd edn. Series in Computational and Physical Processes in Mechanics and Thermal Sciences. CRC Press.Google Scholar
Vanella, M., Piomelli, U. & Balaras, E. 2008 Effect of grid discontinuities on large-eddy simulation statistics and flow fields. J. Turbul. 9 (32), 1–23.Google Scholar
van Leer, B. 1977 Towards the ultimate conservative difference scheme III. Upstream-centered finite-difference schemes for ideal compressible flow. J. Comput. Phys. 23, 263–275.CrossRefGoogle Scholar
Williams, F. A. 1985 Combustion Theory, 2nd edn. Benjamin/Cummings Publishing Company Inc.Google Scholar
Ziegler, J. L., Deiterding, R., Shepherd, J. E. & Pullin, D. I. 2011 An adaptive high-order hybrid scheme for compressive, viscous flows with detailed chemistry. J. Comput. Phys. 230, 7598–7630.Google Scholar