Hostname: page-component-586b7cd67f-2plfb Total loading time: 0 Render date: 2024-11-21T06:34:38.503Z Has data issue: false hasContentIssue false
  • English
  • Français

Inner–outer interactions of large-scale structures in turbulent channel flow

Published online by Cambridge University Press:  02 February 2016

Jinyul Hwang ,
Jin Lee ,
Hyung Jin Sung  and
Tamer A. Zaki
Jinyul Hwang
Affiliation:
Department of Mechanical Engineering, KAIST, 291 Daehak-ro, Yuseong-gu, Daejeon 34141, Korea
Jin Lee
Affiliation:
Department of Mechanical Engineering, KAIST, 291 Daehak-ro, Yuseong-gu, Daejeon 34141, Korea Department of Mechanical Engineering, Johns Hopkins University, Baltimore, MD 21218, USA
Hyung Jin Sung*
Affiliation:
Department of Mechanical Engineering, KAIST, 291 Daehak-ro, Yuseong-gu, Daejeon 34141, Korea
Tamer A. Zaki
Affiliation:
Department of Mechanical Engineering, Johns Hopkins University, Baltimore, MD 21218, USA
*
†Email address for correspondence: hjsung@kaist.ac.kr
Get access Rights & Permissions [Opens in a new window]

Abstract

Direct numerical simulation data of turbulent channel flow (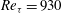$Re_{{\it\tau}}=930$) are used to investigate the statistics of long motions of streamwise velocity fluctuations ($u$), and the interaction of these structures with the near-wall disturbances, which is facilitated by their associated large-scale circulations. In the log layer, the negative-$u$ structures are organized into longer streamwise extent (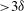${>}3{\it\delta}$) in comparison to the positive-$u$ counterparts. Near the wall, the footprint of negative-$u$ structures is relatively narrow in comparison to the footprint of positive-$u$ structures. This difference is due to the opposite spanwise motions in the vicinity of the footprints, which are either congregative or dispersive depending on the circulation of the outer roll cells. Conditional sampling of the footprints shows that the spanwise velocity fluctuations (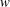$w$) are significantly enhanced by the dispersive motions of high-speed structures. On the other hand, the near-wall congregative motions of negative-$u$ structures generate relatively weak 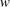$w$ but intense negative-$u$ regions due, in part, to the spanwise collective migration of near-wall streaks. The concentrated near-wall regions of negative-$u$ upwell during the merging of the outer long scales – an effect that is demonstrated using statistical analysis of the merging process. This leads to a reduction of the convection speed of downstream negative-$u$ structures and thus promotes the merging with upstream ones. These top-down and bottom-up interactions enhance the spatial coherence of long negative-$u$ structures in the log region.

JFM classification

Turbulent Flows: Turbulence simulation Turbulent Flows: Turbulent boundary layers Turbulent Flows: Turbulent Flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 790 , 10 March 2016 , pp. 128 - 157
Check for updates
Copyright
© 2016 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Adrian, R. J. 2007 Hairpin vortex organization in wall turbulence. Phys. Fluids 19 (4), 041301.Google Scholar
Adrian, R. J., Meinhart, C. D. & Tomkins, C. D. 2000 Vortex organization in the outer region of the turbulent boundary layer. J. Fluid Mech. 422, 1–54.Google Scholar
Agostini, L. & Leschziner, M. A. 2014 On the influence of outer large-scale structures on near-wall turbulence in channel flow. Phys. Fluids 26 (7), 075107.Google Scholar
Ahn, J., Lee, J. H., Lee, J., Kang, J.-H & Sung, H. J. 2015 Direct numerical simulation of a $30R$ long turbulent pipe flow at $Re_{{\it\tau}}=3008$ . Phys. Fluids 27 (6), 065110.Google Scholar
del Álamo, J. C. & Jiménez, J. 2003 Spectra of the very large anisotropic scales in turbulent channels. Phys. Fluids 15 (6), L41.Google Scholar
del Álamo, J. C. & Jiménez, J. 2006 Linear energy amplification in turbulent channels. J. Fluid Mech. 559, 205–213.Google Scholar
Balakumar, B. J. & Adrian, R. J. 2007 Large- and very-large-scale motions in channel and boundary-layer flows. Phil. Trans. R. Soc. Lond. A 365 (1852), 665–681.Google Scholar
Baltzer, J. R., Adrian, R. J. & Wu, X. 2013 Structural organization of large and very large scales in turbulent pipe flow simulation. J. Fluid Mech. 720, 236–279.Google Scholar
Chung, D. & McKeon, B. J. 2010 Large-eddy simulation of large-scale structures in long channel flow. J. Fluid Mech. 661, 341–364.Google Scholar
Dennis, D. J. C. & Nickels, T. B. 2011 Experimental measurement of large-scale three-dimensional structures in a turbulent boundary layer. Part 2. Long structures. J. Fluid Mech. 673, 218–244.Google Scholar
Ganapathisubramani, B. 2008 Statistical structure of momentum sources and sinks in the outer region of a turbulent boundary layer. J. Fluid Mech. 606, 225–237.Google Scholar
Ganapathisubramani, B., Hutchins, N., Monty, J. P., Chung, D. & Marusic, I. 2012 Amplitude and frequency modulation in wall turbulence. J. Fluid Mech. 712, 61–91.Google Scholar
Ganapathisubramani, B., Longmire, E. K. & Marusic, I. 2003 Characteristics of vortex packets in turbulent boundary layers. J. Fluid Mech. 478, 35–46.Google Scholar
Guala, M., Hommema, S. E. & Adrian, R. J. 2006 Large-scale and very-large-scale motions in turbulent pipe flow. J. Fluid Mech. 554, 521–542.Google Scholar
Hoyas, S. & Jiménez, J. 2006 Scaling of the velocity fluctuations in turbulent channels up to $Re_{{\it\tau}}=2003$ . Phys. Fluids 18 (1), 011702.Google Scholar
Hutchins, N. & Marusic, I. 2007a Evidence of very long meandering features in the logarithmic region of turbulent boundary layers. J. Fluid Mech. 579, 1–28.Google Scholar
Hutchins, N. & Marusic, I. 2007b Large-scale influences in near-wall turbulence. Phil. Trans. R. Soc. Lond. A 365 (1852), 647–664.Google Scholar
Hwang, Y. & Cossu, C. 2010 Self-sustained process at large scales in turbulent channel flow. Phys. Rev. Lett. 105 (4), 044505.Google Scholar
Kim, K., Baek, S. J. & Sung, H. J. 2002 An implicit velocity decoupling procedure for the incompressible Navier–Stokes equations. Intl J. Numer. Meth. Fluids 38 (2), 125–138.Google Scholar
Kim, K. C. & Adrian, R. J. 1999 Very large-scale motion in the outer layer. Phys. Fluids 11 (2), 417–422.Google Scholar
Lee, J., Ahn, J. & Sung, H. J. 2015 Comparison of large- and very-large-scale motions in turbulent pipe and channel flows. Phys. Fluids 27 (2), 025101.Google Scholar
Lee, J., Lee, J. H., Choi, J.-I. & Sung, H. J. 2014 Spatial organization of large-and very-large-scale motions in a turbulent channel flow. J. Fluid Mech. 749, 818–840.Google Scholar
Lee, J. H. & Sung, H. J. 2011 Very-large-scale motions in a turbulent boundary layer. J. Fluid Mech. 673, 80–120.Google Scholar
Lee, J. H. & Sung, H. J. 2013 Comparison of very-large-scale motions of turbulent pipe and boundary layer simulations. Phys. Fluids 25 (4), 045103.Google Scholar
Liu, Z., Adrian, R. J. & Hanratty, T. J. 2001 Large-scale modes of turbulent channel flow: transport and structure. J. Fluid Mech. 448, 53–80.Google Scholar
Mathis, R., Hutchins, N. & Marusic, I. 2009 Large-scale amplitude modulation of the small-scale structures in turbulent boundary layers. J. Fluid Mech. 628, 311–337.Google Scholar
McKeon, B. J. & Sharma, A. S. 2010 A critical-layer framework for turbulent pipe flow. J. Fluid Mech. 658, 336–382.Google Scholar
Mito, Y., Hanratty, T. J., Zandonade, P. & Moser, R. D. 2007 Flow visualization of superbursts and of the log-layer in a DNS at $Re_{{\it\tau}}=950$ . Flow Turbul. Combust. 79 (2), 175–189.Google Scholar
Monty, J. P., Hutchins, N., Ng, H. C. H., Marusic, I. & Chong, M. S. 2009 A comparison of turbulent pipe, channel and boundary layer flows. J. Fluid Mech. 632, 431–442.Google Scholar
Monty, J. P., Stewart, J. A., Williams, R. C. & Chong, M. S. 2007 Large-scale features in turbulent pipe and channel flows. J. Fluid Mech. 589, 147–156.Google Scholar
Nolan, K. P. & Zaki, T. A. 2013 Conditional sampling of transitional boundary layers in pressure gradients. J. Fluid Mech. 728, 306–339.Google Scholar
Sillero, J. A., Jiménez, J. & Moser, R. D. 2014 Two-point statistics for turbulent boundary layers and channels at Reynolds numbers up to ${\it\delta}^{+}=2000$ . Phys. Fluids 26 (10), 105109.Google Scholar
Talluru, K. M., Baidya, R., Hutchins, N. & Marusic, I. 2014 Amplitude modulation of all three velocity components in turbulent boundary layers. J. Fluid Mech. 746, R1.Google Scholar
Toh, S. & Itano, T. 2005 Interaction between a large-scale structure and near-wall structures in channel flow. J. Fluid Mech. 524, 249–262.Google Scholar
Tomkins, C. D. & Adrian, R. J. 2003 Spanwise structure and scale growth in turbulent boundary layers. J. Fluid Mech. 490, 37–74.Google Scholar
Wallace, J. M., Eckelmann, H. & Brodkey, R. S. 1972 The wall region in turbulent shear flow. J. Fluid Mech. 54 (01), 39–48.Google Scholar
Wu, X., Baltzer, J. R. & Adrian, R. J. 2012 Direct numerical simulation of a $30R$ long turbulent pipe flow at $R^{+}=685$ : large- and very large-scale motions. J. Fluid Mech. 698, 235–281.Google Scholar
Zaki, T. A. 2013 From streaks to spots and on to turbulence: exploring the dynamics of boundary layer transition. Flow Turbul. Combust. 91 (3), 451–473.Google Scholar
Zhou, J., Adrian, R. J., Balachandar, S. & Kendall, T. M. 1999 Mechanisms for generating coherent packets of hairpin vortices in channel flow. J. Fluid Mech. 387, 353–396.Google Scholar

Hwang Supplementary Material

Movie 1: Time sequence of instantaneous flow fields before the merging event.

Download Hwang Supplementary Material(Video)
Video 1.8 MB

Hwang Supplementary Material

Movie 2: Time sequence of instantaneous flow fields before the merging event.

Download Hwang Supplementary Material(Video)
Video 2.1 MB