Hostname: page-component-586b7cd67f-rdxmf Total loading time: 0 Render date: 2024-12-01T05:43:43.990Z Has data issue: false hasContentIssue false
  • English
  • Français

Interfacial instability at a heavy/light interface induced by rarefaction waves

Published online by Cambridge University Press:  07 January 2020

Yu Liang Open the ORCID record for Yu Liang [Opens in a new window] ,
Zhigang Zhai Open the ORCID record for Zhigang Zhai [Opens in a new window] ,
Xisheng Luo Open the ORCID record for Xisheng Luo [Opens in a new window]  and
Chih-yung Wen Open the ORCID record for Chih-yung Wen [Opens in a new window]
Yu Liang
Affiliation:
Advanced Propulsion Laboratory, Department of Modern Mechanics, University of Science and Technology of China, Hefei230026, China Department of Mechanical Engineering and Interdisplinary Division of Aeronautical and Aviation Engineering, The Hong Kong Polytechnic University, Kowloon, Hong Kong
Zhigang Zhai
Affiliation:
Advanced Propulsion Laboratory, Department of Modern Mechanics, University of Science and Technology of China, Hefei230026, China
Xisheng Luo
Affiliation:
Advanced Propulsion Laboratory, Department of Modern Mechanics, University of Science and Technology of China, Hefei230026, China
Chih-yung Wen*
Affiliation:
Department of Mechanical Engineering and Interdisplinary Division of Aeronautical and Aviation Engineering, The Hong Kong Polytechnic University, Kowloon, Hong Kong
*
†Email address for correspondence: chihyung.wen@polyu.edu.hk
Get access Rights & Permissions [Opens in a new window]

Abstract

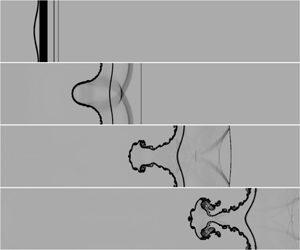
The interaction of rarefaction waves and a heavy/light interface is investigated using numerical simulations by solving the compressible Euler equations. An upwind space–time conservation element and solution element (CE/SE) scheme with second-order accuracy in both space and time is adopted. Rarefaction waves are generated by simulating the shock-tube problem. In this work, the SF6/air interface evolution under different conditions is considered. First, the gas physical parameters before and after the rarefaction waves impact the interface are calculated using one-dimensional gas dynamics theory. Then, the interaction between the rarefaction waves and a single-mode perturbation interface is investigated, and both the interface evolution and the wave patterns are obtained. Afterwards, the amplitude growth of the interface over time is compared between cases, considering the effects of the interaction period and the strength of the rarefaction waves. During the interaction of the rarefaction waves with the interface, the Rayleigh–Taylor instability induced by the rarefaction waves is well predicted by modifying the nonlinear model proposed by Zhang & Guo (J. Fluid Mech., vol. 786, 2016, pp. 47–61), considering the variable acceleration. After the rarefaction waves leave the interface, the equivalent Richtmyer–Meshkov instability is well depicted by the nonlinear model proposed by Zhang et al. (Phys. Rev. Lett., vol. 121(17), 2018, 174502), considering the growth rate transition from Rayleigh–Taylor instability to Richtmyer–Meshkov instability. The differences in the heavy/light interface amplitude growth under the rarefaction wave condition and the shock wave condition are compared. The interface perturbation is shown to be more unstable under rarefaction waves than under a shock wave.

JFM classification

Compressible Flows: Gas dynamics Instability: Nonlinear instability
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 885 , 25 February 2020 , A42
Copyright
© The Author(s), 2020. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abgrall, R. 1996 How to prevent pressure oscillations in multicomponent flow calculations: a quasi conservative approach. J. Comput. Phys. 125 (1), 150–160.CrossRefGoogle Scholar
Brouillette, M. 2002 The Richtmyer–Meshkov instability. Annu. Rev. Fluid Mech. 34, 445–468.CrossRefGoogle Scholar
Collins, B. D. & Jacobs, J. W. 2002 PLIF flow visualization and measurements of the Richtmyer–Meshkov instability of an air/SF6 interface. J. Fluid Mech. 464, 113–136.CrossRefGoogle Scholar
Dell, Z., Stellingwerf, R. F. & Abarzhi, S. I. 2015 Effect of initial perturbation amplitude on Richtmyer–Meshkov flows induced by strong shocks. Phys. Plasmas 22 (9), 092711.CrossRefGoogle Scholar
Desse, J. M. & Deron, R. 2009 Shadow, Schlieren and color interferometry. AerospaceLab hal‐01180681 (1), 1–10.Google Scholar
Fan, E., Guan, B., Wen, C. Y. & Shen, H. 2019 Numerical study on the jet formation of simple-geometry heavy gas inhomogeneities. Phys. Fluids 31, 026103.CrossRefGoogle Scholar
Guan, B., Liu, Y., Wen, C. Y. & Shen, H. 2018 Numerical study on liquid droplet internal flow under shock impact. AIAA J. 56 (9), 3382–3387.CrossRefGoogle Scholar
Han, Z. & Yin, X. 1992 Shock Dynamics. Science.Google Scholar
Holmes, R. L., Dimonte, G., Fryxell, B., Gittings, M. L., Grove, J. W., Schneider, M., Sharp, D. H., Velikovich, A. L., Weaver, R. P. & Zhang, Q. 1999 Richtmyer–Meshkov instability growth: experiment, simulation and theory. J. Fluid Mech. 389, 55–79.CrossRefGoogle Scholar
Jacobs, J. W. & Krivets, V. V. 2005 Experiments on the late-time development of single-mode Richtmyer–Meshkov instability. Phys. Fluids 17 (3), 034105.CrossRefGoogle Scholar
Kuranz, C. C., Drake, R. P., Harding, E. C., Grosskopf, M. J., Robey, H. F., Remington, B. A., Edwards, M. J., Miles, A. R., Perry, T. S., Blue, B. E. et al. 2009 Two-dimensional blast-wave-driven Rayleigh–Taylor instability: experiment and simulation. Astrophys. J. 696 (1), 749.CrossRefGoogle Scholar
Latini, M. & Schilling, O. 2020 A comparison of two- and three-dimensional single-mode reshocked Richtmyer–Meshkov instability growth. Physica D 401, 132201.Google Scholar
Latini, M., Schilling, O. & Don, W. S. 2007 High-resolution simulations and modeling of reshocked single-mode Richtmyer–Meshkov instability: comparison to experimental data and to amplitude growth model predictions. Phys. Fluids 19 (2), 024104.CrossRefGoogle Scholar
Li, C. & Book, D. L. 1991 Instability generated by acceleration due to rarefaction waves. Phys. Rev. A 43 (6), 3153.CrossRefGoogle ScholarPubMed
Li, C., Kailasanath, K. & Book, D. L. 1991 Mixing enhancement by expansion waves in supersonic flows of different densities. Phys. Fluids A 3 (5), 1369–1373.CrossRefGoogle Scholar
Lindl, J. D., Landen, O., Edwards, J., Moses, E. & NIC Team 2014 Review of the national ignition campaign 2009–2012. Phys. Plasmas 21 (2), 020501.CrossRefGoogle Scholar
Liu, L., Liang, Y., Ding, J., Liu, N. & Luo, X. 2018 An elaborate experiment on the single-mode Richtmyer–Meshkov instability. J. Fluid Mech. 853, R2.CrossRefGoogle Scholar
Meshkov, E. E. 1969 Instability of the interface of two gases accelerated by a shock wave. Fluid Dyn. 4 (5), 101–104.CrossRefGoogle Scholar
Miles, A. R., Edwards, M. J., Blue, B., Hansen, J. F., Robey, H. F., Drake, R. P., Kuranz, C. & Leibrandt, D. R. 2004 The effect of a short-wavelength mode on the evolution of a long-wavelength perturbation driven by a strong blast wave. Phys. Plasmas 11 (12), 5507–5519.CrossRefGoogle Scholar
Morgan, R. V., Cabot, W. H., Greenough, J. A. & Jacobs, J. W. 2018 Rarefaction-driven Rayleigh–Taylor instability. Part 2. Experiments and simulations in the nonlinear regime. J. Fluid Mech. 838, 320–355.CrossRefGoogle Scholar
Morgan, R. V., Likhachev, O. A. & Jacobs, J. W. 2016 Rarefaction-driven Rayleigh–Taylor instability. Part 1. Diffuse-interface linear stability measurements and theory. J. Fluid Mech. 791, 34–60.CrossRefGoogle Scholar
Niederhaus, J. H. J., Greenough, J. A., Oakley, J. G., Ranjan, D., Anderson, M. H. & Bonazza, R. 2008 A computational parameter study for the three-dimensional shock–bubble interaction. J. Fluid Mech. 594, 85–124.CrossRefGoogle Scholar
Owczarek, J. A. 1964 Fundamentals of Gas Dynamics. International Textbook Co.Google Scholar
Ranjan, D., Oakley, J. & Bonazza, R. 2011 Shock–bubble interactions. Annu. Rev. Fluid Mech. 43, 117–140.CrossRefGoogle Scholar
Rayleigh, Lord 1883 Investigation of the character of the equilibrium of an incompressible heavy fluid of variable density. Proc. Lond. Math. Soc. 14, 170–177.Google Scholar
Richtmyer, R. D. 1960 Taylor instability in shock acceleration of compressible fluids. Commun. Pure Appl. Maths 13 (2), 297–319.CrossRefGoogle Scholar
Rikanati, A., Oron, D., Sadot, O. & Shvarts, D. 2003 High initial amplitude and high Mach number effects on the evolution of the single-mode Richtmyer–Meshkov instability. Phys. Rev. E 67 (2), 026307.Google ScholarPubMed
Sembian, S., Liverts, M., Tillmark, N. & Apazidis, N. 2016 Plane shock wave interaction with a cylindrical water column. Phys. Fluids 28 (5), 056102.CrossRefGoogle Scholar
Sharp, D. H. 1983 An overview of Rayleigh–Taylor instability. Physica D 12 (1), 3–18.Google Scholar
Shen, H. & Parsani, M. 2017 The role of multidimensional instabilities in direct initiation of gaseous detonations in free space. J. Fluid Mech. 813, R4.CrossRefGoogle Scholar
Shen, H. & Wen, C. Y. 2016 A characteristic space–time conservation element and solution element method for conservation laws II. Multidimensional extension. J. Comput. Phys. 305, 775–792.CrossRefGoogle Scholar
Shen, H., Wen, C. Y., Liu, K. X. & Zhang, D. L. 2015a Robust high-order space–time conservative schemes for solving conservation laws on hybrid meshes. J. Comput. Phys. 281, 375–402.CrossRefGoogle Scholar
Shen, H., Wen, C. Y., Parsani, M. & Shu, C. W. 2017 Maximum-principle-satisfying space–time conservation element and solution element scheme applied to compressible multifluids. J. Comput. Phys. 330, 668–692.CrossRefGoogle Scholar
Shen, H., Wen, C. Y. & Zhang, D. L. 2015b A characteristic space–time conservation element and solution element method for conservation laws. J. Comput. Phys. 288, 101–118.CrossRefGoogle Scholar
Shimoda, J., Inoue, T., Ohira, Y., Yamazaki, R., Bamba, A. & Vink, J. 2015 On cosmic-ray production efficiency at Supernova remnant shocks propagating into realistic diffuse interstellar medium. Astrophys. J. 803 (2), 98–103.CrossRefGoogle Scholar
Shyue, K. M. 1998 An efficient shock-capturing algorithm for compressible multicomponent problems. J. Comput. Phys. 142 (1), 208–242.CrossRefGoogle Scholar
Stanic, M., Stellingwerf, R. F., Cassibry, J. T. & Abarzhi, S. I. 2012 Scale coupling in Richtmyer–Meshkov flows induced by strong shocks. Phys. Plasmas 19 (8), 082706.CrossRefGoogle Scholar
Taylor, G. 1950 The instability of liquid surfaces when accelerated in a direction perpendicular to their planes. I. Proc. R. Soc. Lond. A 201 (1065), 192–196.Google Scholar
Toro, E. F., Spruce, M. & Speares, W. 1994 Restoration of the contact surface in the HLL-Riemann solver. Shock Waves 4 (1), 25–34.CrossRefGoogle Scholar
Velikovich, A. & Phillips, L. 1996 Instability of a plane centered rarefaction wave. Phys. Fluids 8 (4), 1107–1118.CrossRefGoogle Scholar
Zhai, Z., Zhang, F., Zhou, Z., Ding, J. & Wen, C. Y. 2019 Numerical study on Rayleigh–Taylor effect on cylindrically converging Richtmyer–Meshkov instability. Sci. China-Phys. Mech. Astron. 62 (12), 124712.CrossRefGoogle Scholar
Zhang, Q., Deng, S. & Guo, W. 2018 Quantitative theory for the growth rate and amplitude of the compressible Richtmyer–Meshkov instability at all density ratios. Phys. Rev. Lett. 121 (17), 174502.CrossRefGoogle ScholarPubMed
Zhang, Q. & Guo, W. 2016 Universality of finger growth in two-dimensional Rayleigh–Taylor and Richtmyer–Meshkov instabilities with all density ratios. J. Fluid Mech. 786, 47–61.CrossRefGoogle Scholar
Zhou, Y. 2017a Rayleigh–Taylor and Richtmyer–Meshkov instability induced flow, turbulence, and mixing. I. Phys. Rep. 720–722, 1–136.Google Scholar
Zhou, Y. 2017b Rayleigh–Taylor and Richtmyer–Meshkov instability induced flow, turbulence, and mixing. II. Phys. Rep. 723–725, 1–160.Google Scholar