Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-26T21:14:41.099Z Has data issue: false hasContentIssue false
  • English
  • Français

Lattice Boltzmann simulation of resolved oblate spheroids in wall turbulence

Published online by Cambridge University Press:  21 June 2018

Amir Eshghinejadfard Open the ORCID record for Amir Eshghinejadfard [Opens in a new window] ,
Lihao Zhao  and
Dominique Thévenin
Amir Eshghinejadfard*
Affiliation:
Laboratory of Fluid Dynamics and Technical Flows, University of Magdeburg ‘Otto von Guericke’, Universitätsplatz 2, 39106 Magdeburg, Germany
Lihao Zhao
Affiliation:
Department of Engineering Mechanics, Tsinghua University, 10084 Beijing, China
Dominique Thévenin
Affiliation:
Laboratory of Fluid Dynamics and Technical Flows, University of Magdeburg ‘Otto von Guericke’, Universitätsplatz 2, 39106 Magdeburg, Germany
*
†Email address for correspondence: amir.eshghinejadfard@ovgu.de
Get access Rights & Permissions [Opens in a new window]

Abstract

The present study focuses on the behaviour of fully resolved oblate spheroids in turbulent channel flows using the lattice Boltzmann method (LBM). Mean and maximum drag reductions of 1.3 % and 4.4 %, respectively, are observed at a solid-phase volume fraction of 10 % by using oblate spheroids of aspect ratio 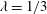$\unicode[STIX]{x1D706}=1/3$ and equivalent diameter 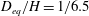$D_{eq}/H=1/6.5$. The behaviour of oblate spheroids and spheres are found to be different in the near-wall region, where oblate spheroids, in contrast to spheres, do not augment the near-wall turbulence. Strong reduction of spanwise and wall-normal fluid velocity fluctuations in the buffer layer by using oblate spheroids is observed. It is also seen that reduction of Reynolds shear stress cannot solely guarantee the occurrence of drag reduction, as spherical particles increase the drag in spite of the reduction in Reynolds shear stress. Moreover, in drag-reduced particle-laden flows, although the spanwise spacing of streaks increases, vortices are stronger and smaller. Thus, in addition to the streak cycle of turbulence regeneration, the vortices generated by particles contribute to higher vortex strengths. By examining the role of the oblate spheroid concentration, it is found to mainly influence the streak spacing, with a minor effect on the strength of vortices. Drag reduction in oblate-spheroid-laden flows is thus attributed to the reduction of fluid velocity fluctuations in the transverse directions and enhancement of the spanwise streak spacing. Higher vortex strength has less effect on the initiation of drag reduction but can influence the level of drag reduction and explains the lower drag-reduction effect of rigid particles compared to polymers. By quadrant analysis, sweeps and ejections are seen to have less contribution to the Reynolds shear stress by using oblate spheroids. With respect to the particle data, oblate spheroids tend to orient with their symmetry axis mainly along the wall-normal direction. Very close to the wall, spanwise orientation is dominant and wall-normal alignment of the symmetry axis is reduced. Furthermore, oblate spheroids move faster than the fluid, before reaching a similar streamwise velocity in the channel centre. In contrast, spheres move slower than the fluid in the buffer region, as well as showing a local concentration peak near the wall. It is also seen that the angular velocity of oblate spheroids decays very rapidly whereas spheres have a higher rotation rate which shows a smoother reduction towards the centre.

JFM classification

Flow Control: Drag reduction Multiphase and Particle-laden Flows: Multiphase flow Multiphase and Particle-laden Flows: Particle/fluid flow
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 849 , 25 August 2018 , pp. 510 - 540
Check for updates
Copyright
© 2018 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Andersson, H. I., Zhao, L. & Barri, M. 2012 Torque-coupling and particle–turbulence interactions. J. Fluid Mech. 696, 319–329.Google Scholar
Ardekani, M. N., Costa, P., Breugem, W.-P., Picano, F. & Brandt, L. 2017 Drag reduction in turbulent channel flow laden with finite-size oblate spheroids. J. Fluid Mech. 816, 43–70.Google Scholar
Balachandar, S. & Eaton, J. K. 2010 Turbulent dispersed multiphase flow. Annu. Rev. Fluid Mech. 42, 111–133.Google Scholar
Bhatnagar, P. L., Gross, E. P. & Krook, M. 1954 A model for collision processes in gases. Part I. Small amplitude processes in charged and neutral one-component systems. Phys. Rev. 94 (3), 511–525.Google Scholar
Brenner, H. 1964 The Stokes resistance of an arbitrary particle. Part IV. Arbitrary fields of flow. Chem. Engng Sci. 19, 703–727.Google Scholar
Brooke, J. W. & Hanratty, T. J. 1993 Origin of turbulence-producing eddies in a channel flow. Phys. Fluids A 5, 1011–1022.Google Scholar
Burton, T. M. & Eaton, J. K. 2005 Fully resolved simulations of particle–turbulence interaction. J. Fluid Mech. 545, 67–111.Google Scholar
Challabotla, N. R., Nilsen, C. & Andersson, H. I. 2015a On rotational dynamics of inertial disks in creeping shear flow. Phys. Lett. A 379, 157–162.Google Scholar
Challabotla, N. R., Zhao, L. & Andersson, H. I. 2015b Orientation and rotation of inertial disk particles in wall turbulence. J. Fluid Mech. 766, R2.Google Scholar
Challabotla, N. R., Zhao, L. & Andersson, H. I. 2015c Shape effects on dynamics of inertia-free spheroids in wall turbulence. Phys. Fluids 27, 061703.Google Scholar
Choi, H., Moin, P. & Kim, J. 1993 Direct numerical simulation of turbulent flow over riblets. J. Fluid Mech. 255, 503–539.Google Scholar
Clift, R., Grace, J. R. & Weber, M. E. 2005 Bubbles, Drops, and Particles. Courier Corporation.Google Scholar
Den Toonder, J. M. J., Hulsen, M. A., Kuiken, G. D. C. & Nieuwstadt, F. T. M. 1997 Drag reduction by polymer additives in a turbulent pipe flow: numerical and laboratory experiments. J. Fluid Mech. 337, 193–231.Google Scholar
Ding, E. & Aidun, C. K. 2000 The dynamics and scaling law for particles suspended in shear flow with inertia. J. Fluid Mech. 423, 317–344.Google Scholar
Do-Quang, M., Amberg, G., Brethouwer, G. & Johansson, A. V. 2014 Simulation of finite-size fibers in turbulent channel flows. Phys. Rev. E 89, 013006.Google Scholar
Dubief, Y. & Lele, S. K. 2001 Direct numerical simulation of polymer flow. In Center for Turbulence Research: Annual Research Briefs, pp. 197–208. NASA Ames/Stanford University.Google Scholar
Elghobashi, S. 2006 An updated classification map of particle-laden turbulent flows. In IUTAM Symposium on Computational Approaches to Multiphase Flow, pp. 3–10. Springer.Google Scholar
Escudier, M. P., Nickson, A. K. & Poole, R. J. 2009 Turbulent flow of viscoelastic shear-thinning liquids through a rectangular duct: quantification of turbulence anisotropy. J. Non-Newtonian Fluid Mech. 160, 2–10.Google Scholar
Eshghinejadfard, A., Abdelsamie, A., Hosseini, S. A. & Thévenin, D. 2017a Immersed boundary lattice Boltzmann simulation of turbulent channel flows in the presence of spherical particles. Intl J. Multiphase Flow 96, 161–172.Google Scholar
Eshghinejadfard, A., Abdelsamie, A., Janiga, G. & Thévenin, D. 2016 Direct-forcing immersed boundary lattice Boltzmann simulation of particle/fluid interactions for spherical and non-spherical particles. Particuology 25, 93–103.Google Scholar
Eshghinejadfard, A., Hosseini, S. A. & Thévenin, D. 2017b Fully-resolved prolate spheroids in turbulent channel flows: a lattice Boltzmann study. AIP Advances 7, 095007.Google Scholar
Feng, Z.-G. & Michaelides, E. E. 2005 Proteus: a direct forcing method in the simulations of particulate flows. J. Comput. Phys. 202, 20–51.Google Scholar
Fornari, W., Formenti, A., Picano, F. & Brandt, L. 2016 The effect of particle density in turbulent channel flow laden with finite size particles in semi-dilute conditions. Phys. Fluids 28, 033301.Google Scholar
Glowinski, R., Pan, T.-W., Hesla, T. I. & Joseph, D. D. 1999 A distributed Lagrange multiplier/fictitious domain method for particulate flows. Intl J. Multiphase Flow 25, 755–794.Google Scholar
Hammond, E. P., Bewley, T. R. & Moin, P. 1998 Observed mechanisms for turbulence attenuation and enhancement in opposition-controlled wall-bounded flows. Phys. Fluids 10, 2421–2423.Google Scholar
Hölzer, A. & Sommerfeld, M. 2008 New simple correlation formula for the drag coefficient of non-spherical particles. Powder Technol. 184, 361–365.Google Scholar
Huang, H., Yang, X., Krafczyk, M. & Lu, X.-Y. 2012 Rotation of spheroidal particles in Couette flows. J. Fluid Mech. 692, 369–394.Google Scholar
Jeffery, G. B. 1922 The motion of ellipsoidal particles immersed in a viscous fluid. Proc. R. Soc. Lond. A 102, 161–179.Google Scholar
Jiménez, J. & Moin, P. 1991 The minimal flow unit in near-wall turbulence. J. Fluid Mech. 225, 213–240.Google Scholar
Jiménez, J. & Pinelli, A. 1999 The autonomous cycle of near-wall turbulence. J. Fluid Mech. 389, 335–359.Google Scholar
Kempe, T., Schwarz, St. & Fröhlich, J. 2009 Modelling of spheroidal particles in viscous flows. In Proceedings of the Academy Colloquium Immersed Boundary Methods: Current Status and Future Research Directions (KNAW, Amsterdam, The Netherlands, 15–17 June 2009), vol. 845. EUROMECH/ERCOFTAC.Google Scholar
Kim, J. 2011 Physics and control of wall turbulence for drag reduction. Phil. Trans. R. Soc. Lond. A 369, 1396–1411.Google Scholar
Kim, J., Moin, P. & Moser, R. 1987 Turbulence statistics in fully developed channel flow at low Reynolds number. J. Fluid Mech. 177, 133–166.Google Scholar
Kulick, J. D., Fessler, J. R. & Eaton, J. K. 1994 Particle response and turbulence modification in fully developed channel flow. J. Fluid Mech. 277, 109–134.Google Scholar
Ladd, A. J. C. & Verberg, R. 2001 Lattice–Boltzmann simulations of particle–fluid suspensions. J. Stat. Phys. 104 (5–6), 1191–1251.Google Scholar
Lee, J. & Lee, C. 2015 Modification of particle-laden near-wall turbulence: effect of Stokes number. Phys. Fluids 27, 023303.Google Scholar
Loisel, V., Abbas, M., Masbernat, O. & Climent, E. 2013 The effect of neutrally buoyant finite-size particles on channel flows in the laminar–turbulent transition regime. Phys. Fluids 25, 123304.Google Scholar
Lumley, J. L. 1969 Drag reduction by additives. Annu. Rev. Fluid Mech. 1, 367–384.Google Scholar
Mandø, M. & Rosendahl, L. 2010 On the motion of non-spherical particles at high Reynolds number. Powder Technol. 202, 1–13.Google Scholar
Mao, W. & Alexeev, A. 2014 Motion of spheroid particles in shear flow with inertia. J. Fluid Mech. 749, 145–166.Google Scholar
Marchioli, C., Fantoni, M. & Soldati, A. 2010 Orientation, distribution, and deposition of elongated, inertial fibers in turbulent channel flow. Phys. Fluids 22 (3), 033301.Google Scholar
Marchioli, C. & Soldati, A. 2002 Mechanisms for particle transfer and segregation in a turbulent boundary layer. J. Fluid Mech. 468, 283–315.Google Scholar
Marchioli, C. & Soldati, A. 2013 Rotation statistics of fibers in wall shear turbulence. Acta Mechanica 224 (10), 2311–2329.Google Scholar
Matas, J.-P., Morris, J. F. & Guazzelli, E. 2003 Transition to turbulence in particulate pipe flow. Phys. Rev. Lett. 90, 014501.Google Scholar
Min, T., Yul Yoo, J., Choi, H. & Joseph, D. D. 2003 Drag reduction by polymer additives in a turbulent channel flow. J. Fluid Mech. 486, 213–238.Google Scholar
Moosaie, A. & Manhart, M. 2015 On the structure of vorticity and near-wall partial enstrophy in fibrous drag-reduced turbulent channel flow. J. Non-Newtonian Fluid Mech. 223, 249–256.Google Scholar
Mortensen, P. H., Andersson, H. I., Gillissen, J. J. J. & Boersma, B. J. 2008 Dynamics of prolate ellipsoidal particles in a turbulent channel flow. Phys. Fluids 20 (9), 093302.Google Scholar
Moser, R. D., Kim, J. & Mansour, N. N. 1999 Direct numerical simulation of turbulent channel flow up to Re 𝜏 = 590. Phys. Fluids 11, 943–945.Google Scholar
Ni, R., Ouellette, N. T. & Voth, G. A. 2014 Alignment of vorticity and rods with Lagrangian fluid stretching in turbulence. J. Fluid Mech. 743, R3.Google Scholar
Orlandi, P. & Jiménez, J. 1994 On the generation of turbulent wall friction. Phys. Fluids 6, 634–641.Google Scholar
Pan, Y. & Banerjee, S. 1996 Numerical simulation of particle interactions with wall turbulence. Phys. Fluids 8 (10), 2733–2755.Google Scholar
Paschkewitz, J. S., Dubief, Y., Dimitropoulos, C. D., Shaqfeh, E. S. G. & Moin, P. 2004 Numerical simulation of turbulent drag reduction using rigid fibres. J. Fluid Mech. 518, 281–317.Google Scholar
Pereira, A. S. & Soares, E. J. 2012 Polymer degradation of dilute solutions in turbulent drag reducing flows in a cylindrical double gap rheometer device. J. Non-Newtonian Fluid Mech. 179, 9–22.Google Scholar
Peskin, C. S. 2002 The immersed boundary method. Acta Numerica 11, 479–517.Google Scholar
Picano, F., Breugem, W.-P. & Brandt, L. 2015 Turbulent channel flow of dense suspensions of neutrally buoyant spheres. J. Fluid Mech. 764, 463–487.Google Scholar
Ptasinski, P. K., Boersma, B. J., Nieuwstadt, F. T. M., Hulsen, M. A., Van den Brule, B. H. A. A. & Hunt, J. C. R. 2003 Turbulent channel flow near maximum drag reduction: simulations, experiments and mechanisms. J. Fluid Mech. 490, 251–291.Google Scholar
Ptasinski, P. K., Nieuwstadt, F. T. M., Van Den Brule, B. H. A. A. & Hulsen, M. A. 2001 Experiments in turbulent pipe flow with polymer additives at maximum drag reduction. Flow Turbul. Combust. 66, 159–182.Google Scholar
Robinson, S. K. 1991 Coherent motions in the turbulent boundary layer. Annu. Rev. Fluid Mech. 23, 601–639.Google Scholar
Rosén, T., Do-Quang, M., Aidun, C. K. & Lundell, F. 2015 Effect of fluid and particle inertia on the rotation of an oblate spheroidal particle suspended in linear shear flow. Phys. Rev. E 91, 053017.Google Scholar
Rosén, T., Lundell, F. & Aidun, C. K. 2014 Effect of fluid inertia on the dynamics and scaling of neutrally buoyant particles in shear flow. J. Fluid Mech. 738, 563–590.Google Scholar
Shan, X. & Chen, H. 1993 Lattice Boltzmann model for simulating flows with multiple phases and components. Phys. Rev. E 47, 1815–1819.Google Scholar
Shao, X., Wu, T. & Yu, Z. 2012 Fully resolved numerical simulation of particle-laden turbulent flow in a horizontal channel at a low Reynolds number. J. Fluid Mech. 693, 319–344.Google Scholar
Tiong, A. N. T., Kumar, P. & Saptoro, A. 2015 Reviews on drag reducing polymers. Korean J. Chem. Engng 32, 1455–1476.Google Scholar
Toms, B. A. 1948 Some observations on the flow of linear polymer solutions through straight tubes at large Reynolds numbers. In Proceedings of the 1st International Congress on Rheology, vol. 2, pp. 135–141. North-Holland.Google Scholar
Uhlmann, M. 2005 An immersed boundary method with direct forcing for the simulation of particulate flows. J. Comput. Phys. 209, 448–476.Google Scholar
Uhlmann, M. 2008 Interface-resolved direct numerical simulation of vertical particulate channel flow in the turbulent regime. Phys. Fluids 20, 053305.Google Scholar
Verlet, L. 1967 Computer ‘experiments’ on classical fluids. Part I. Thermodynamical properties of Lennard–Jones molecules. Phys. Rev. 159, 98–103.Google Scholar
Voth, G. A. 2015 Disks aligned in a turbulent channel. J. Fluid Mech. 772, 1–4.Google Scholar
Voth, G. A. & Soldati, A. 2017 Anisotropic particles in turbulence. Annu. Rev. Fluid Mech. 49, 249–276.Google Scholar
Vowinckel, B., Kempe, T. & Fröhlich, J. 2014 Fluid–particle interaction in turbulent open channel flow with fully-resolved mobile beds. Adv. Water Resour. 72, 32–44.Google Scholar
Wang, Y.-S., Huang, W.-X. & Xu, C.-X. 2016 Active control for drag reduction in turbulent channel flow: the opposition control schemes revisited. Fluid Dyn. Res. 48, 055501.Google Scholar
Wang, L.-P., Peng, C., Guo, Z. & Yu, Z. 2016 Lattice Boltzmann simulation of particle-laden turbulent channel flow. Comput. Fluids 124, 226–236.Google Scholar
White, C. M. & Mungal, M. G. 2008 Mechanics and prediction of turbulent drag reduction with polymer additives. Annu. Rev. Fluid Mech. 40, 235–256.Google Scholar
White, C. M., Somandepalli, V. S. R. & Mungal, M. G. 2004 The turbulence structure of drag-reduced boundary layer flow. Exp. Fluids 36, 62–69.Google Scholar
Yang, X., Huang, H. & Lu, X. 2015 Sedimentation of an oblate ellipsoid in narrow tubes. Phys. Rev. E 92, 063009.Google Scholar
Yu, Z., Lin, Z., Shao, X. & Wang, L.-P. 2017 Effects of particle–fluid density ratio on the interactions between the turbulent channel flow and finite-size particles. Phys. Rev. E 96, 033102.Google Scholar
Yu, Z., Phan-Thien, N. & Tanner, R. I. 2007 Rotation of a spheroid in a Couette flow at moderate Reynolds numbers. Phys. Rev. E 76, 026310.Google Scholar
Zhang, H., Ahmadi, G., Fan, F.-G. & McLaughlin, J. B. 2001 Ellipsoidal particles transport and deposition in turbulent channel flows. Intl J. Multiphase Flow 27, 971–1009.Google Scholar
Zhang, Q. & Prosperetti, A. 2010 Physics-based analysis of the hydrodynamic stress in a fluid–particle system. Phys. Fluids 22, 033306.Google Scholar
Zhao, L. & Andersson, H. I. 2016 Why spheroids orient preferentially in near-wall turbulence. J. Fluid Mech. 807, 221–234.Google Scholar
Zhao, L., Challabotla, N. R., Andersson, H. I. & Variano, E. A. 2015 Rotation of nonspherical particles in turbulent channel flow. Phys. Rev. Lett. 115, 244501.Google Scholar
Zhao, F., George, W. K. & van Wachem, B. 2015 Four-way coupled simulations of small particles in turbulent channel flow: the effects of particle shape and Stokes number. Phys. Fluids 27 (8), 083301.Google Scholar
Zhao, F. & van Wachem, B. 2013 Direct numerical simulation of ellipsoidal particles in turbulent channel flow. Acta Mechanica 224 (8), 2331–2358.Google Scholar