Hostname: page-component-cb9f654ff-mx8w7 Total loading time: 0 Render date: 2025-08-10T10:21:06.411Z Has data issue: false hasContentIssue false
  • English
  • Français

Local transport of passive scalar released from a point source in a turbulent boundary layer

Published online by Cambridge University Press:  04 May 2018

K. M. Talluru Open the ORCID record for K. M. Talluru [Opens in a new window] ,
J. Philip  and
K. A. Chauhan
K. M. Talluru*
Affiliation:
School of Civil Engineering, University of Sydney, Sydney, NSW 2006, Australia
J. Philip
Affiliation:
Department of Mechanical Engineering, University of Melbourne, Melbourne, VIC 3010, Australia
K. A. Chauhan
Affiliation:
School of Civil Engineering, University of Sydney, Sydney, NSW 2006, Australia
*
†Email address for correspondence: murali.talluru@sydney.edu.au
Get access Rights & Permissions [Opens in a new window]

Abstract

Simultaneous measurements of streamwise velocity (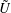$\tilde{U}$ ) and concentration (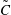$\tilde{C}$ ) for a horizontal plume released at eight different vertical locations within a turbulent boundary layer are discussed in this paper. These are supplemented by limited simultaneous three-component velocity and concentration measurements. Results of the integral time scale (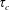$\unicode[STIX]{x1D70F}_{c}$ ) of concentration fluctuations across the width of the plume are presented here for the first time. It is found that 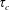$\unicode[STIX]{x1D70F}_{c}$ has two distinct peaks: one closer to the plume centreline and the other at a vertical distance of plume half-width above the centreline. The time-averaged streamwise concentration flux is found to be positive and negative, respectively, below and above the plume centreline. This behaviour is a resultant of wall-normal velocity fluctuations (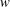$w$ ) and Reynolds shear stress (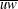$\overline{uw}$ ). Confirmation of these observations is found in the results of joint probability density functions of $u$ (streamwise velocity fluctuations) and 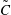$\tilde{C}$ as well as that of 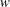$w$ and 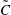$\tilde{C}$ . Results of cross-correlation coefficient show that high- and low-momentum regions have a distinctive role in the transport of passive scalar. Above the plume centreline, low-speed structures have a lead over the meandering plume, while high-momentum regions are seen to lag behind the plume below its centreline. Further examination of the phase relationship between time-varying $u$ and $c$ (concentration fluctuations) via cross-spectrum analysis is consistent with this observation. Based on these observations, a phenomenological model is presented for the relative arrangement of a passive scalar plume with respect to large-scale velocity structures in the flow.

JFM classification

Geophysical and Geological Flows: Atmospheric flows Turbulent Flows: Turbulent boundary layers

Information

Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 846 , 10 July 2018 , pp. 292 - 317
Check for updates
Copyright
© 2018 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Adrian, R. J., Meinhart, C. D. & Tomkins, C. D. 2000 Vortex organization in the outer region of the turbulent boundary layer. J. Fluid Mech. 422, 1–54.CrossRefGoogle Scholar
Antonia, R. A., Danh, H. Q. & Prabhu, A. 1977 Response of a turbulent boundary layer to a step change in surface heat flux. J. Fluid Mech. 80 (1), 153–177.Google Scholar
Arya, S. P. S. 1975 Buoyancy effects in a horizontal flat-plate boundary layer. J. Fluid Mech. 68 (2), 321–343.Google Scholar
Baidya, R., Philip, J., Hutchins, N., Monty, J. P. & Marusic, I. 2017 Distance from the wall scaling of turbulent motions in wall-bounded flows. Phys. Fluids 29 (2), 020712.Google Scholar
Chatwin, P. C. & Sullivan, P. J. 1979 The relative diffusion of a cloud of passive contaminant in incompressible turbulent flow. J. Fluid Mech. 91 (2), 337–355.Google Scholar
Chauhan, K. A., Nagib, H. M. & Monkewitz, P. A. 2009 Criteria for assessing experiments in zero pressure gradient boundary layers. Fluid Dyn. Res. 41, 021404.CrossRefGoogle Scholar
Chauhan, K., Philip, J. & Marusic, I. 2014a Scaling of the turbulent/non-turbulent interface in boundary layers. J. Fluid Mech. 751, 298–328.CrossRefGoogle Scholar
Chauhan, K. A., Philip, J., de Silva, C. M., Hutchins, N. & Marusic, I. 2014b The turbulent/non-turbulent interface and entrainment in a boundary layer. J. Fluid Mech. 742, 119–151.CrossRefGoogle Scholar
Christensen, K. T. & Adrian, R. J. 2001 Statistical evidence of hairpin vortex packets in wall turbulence. J. Fluid Mech. 431, 433–443.Google Scholar
Csanady, G. 1973 Turbulent Diffusion in the Environment. Reidel.Google Scholar
Del Álamo, J. C. & Jiménez, J. 2009 Estimation of turbulent convection velocities and corrections to Taylor’s approximation. J. Fluid Mech. 640, 5–26.CrossRefGoogle Scholar
Dennis, D. J. C. & Nickels, T. B. 2008 On the limitations of Taylor’s hypothesis in constructing long structures in a turbulent boundary layer. J. Fluid Mech. 614, 197–206.Google Scholar
Duplat, J. & Villermaux, E. 2008 Mixing by random stirring in confined mixtures. J. Fluid Mech. 617, 51–86.Google Scholar
Durbin, P. A. 1980 A stochastic model of two-particle dispersion and concentration fluctuations in homogeneous turbulence. J. Fluid Mech. 100 (2), 279–302.CrossRefGoogle Scholar
Fackrell, J. E. 1980 A flame ionisation detector for measuring fluctuating concentration. J. Phys. E: Sci. Instrum. 13 (8), 888.Google Scholar
Fackrell, J. E. & Robins, A. G. 1982 Concentration fluctuations and fluxes in plumes from point sources in a turbulent boundary layer. J. Fluid Mech. 117, 1–26.Google Scholar
Finnigan, J. J., Shaw, R. H. & Patton, E. G. 2009 Turbulence structure above a vegetation canopy. J. Fluid Mech. 637, 387–424.Google Scholar
Gifford, F. 1959 Statistical properties of a fluctuating plume dispersion model. Adv. Geophys. 6, 117–137.Google Scholar
Hay, J. S. & Pasquill, F. 1959 Diffusion from a continuous source in relation to the spectrum and scale of turbulence. Adv. Geophys. 6, 345–365.CrossRefGoogle Scholar
Herpin, S., Stanislas, M., Foucaut, J. M. & Coudert, S. 2013 Influence of the Reynolds number on the vortical structures in the logarithmic region of turbulent boundary layers. J. Fluid Mech. 716, 5–50.Google Scholar
Huang, J., Katul, G. & Albertson, J. 2013 The role of coherent turbulent structures in explaining scalar dissimilarity within the canopy sublayer. Environ. Fluid Mech. 13 (6), 571–599.Google Scholar
Hunt, J. C. R. & Weber, A. H. 1979 A Lagrangian statistical analysis of diffusion from a ground-level source in a turbulent boundary layer. Q. J. R. Meteorol. Soc. 105 (444), 423–443.Google Scholar
Hutchins, N. & Marusic, I. 2007a Evidence of very long meandering features in the logarithmic region of turbulent boundary layers. J. Fluid Mech. 579, 1–28.CrossRefGoogle Scholar
Hutchins, N. & Marusic, I. 2007b Large-scale influences in near-wall turbulence. Phil. Trans. R. Soc. Lond. A 365, 647–664.Google Scholar
Katul, G., Kuhn, G., Schieldge, J. & Hsieh, C. I. 1997 The ejection-sweep character of scalar fluxes in the unstable surface layer. Boundary-Layer Meteorol. 83 (1), 1–26.Google Scholar
Klewicki, J. 2013 Self-similar mean dynamics in turbulent wall flows. J. Fluid Mech. 718, 596–621.Google Scholar
Klewicki, J. C., Murray, J. A. & Falco, R. E. 1994 Vortical motion contributions to stress transport in turbulent boundary layers. Phys. Fluids 6 (1), 277–286.Google Scholar
Krishnamoorthy, L. V. & Antonia, R. A. 1987 Temperature-dissipation measurements in a turbulent boundary layer. J. Fluid Mech. 176, 265–281.Google Scholar
Li, D. & Bou-Zeid, E. 2011 Coherent structures and the dissimilarity of turbulent transport of momentum and scalars in the unstable atmospheric surface layer. Boundary-Layer Meteorol. 140 (2), 243–262.Google Scholar
Marusic, I., McKeon, B. J., Monkewitz, P. A., Nagib, H. M., Smits, A. J. & Sreenivasan, K. R. 2010 Wall-bounded turbulent flows at high Reynolds numbers: recent advances and key issues. Phys. Fluids 22 (6), 065103.CrossRefGoogle Scholar
Mathis, R., Hutchins, N. & Marusic, I. 2009 Large-scale amplitude modulation of the small-scale structures in turbulent boundary layers. J. Fluid Mech. 628, 311–337.Google Scholar
McComb, W. 1990 The Physics of Fluid Turbulence. Oxford University Press.CrossRefGoogle Scholar
Meinhart, C. D. & Adrian, R. J. 1995 On the existence of uniform momentum zones in a turbulent boundary layer. Phys. Fluids 7 (4), 694–696.Google Scholar
Morrill-Winter, C., Philip, J. & Klewicki, J. 2017 An invariant representation of mean inertia: theoretical basis for a log law in turbulent boundary layers. J. Fluid Mech. 813, 594–617.Google Scholar
Nironi, C., Salizzoni, P., Marro, M., Mejean, P., Grosjean, N. & Soulhac, L. 2015 Dispersion of a passive scalar fluctuating plume in a turbulent boundary layer. Part I: Velocity and concentration measurements. Boundary-Layer Meteorol. 156 (3), 415–446.CrossRefGoogle Scholar
Poreh, M. & Cermak, J. E. 1964 Study of diffusion from a line source in a turbulent boundary layer. Intl J. Heat Mass Transfer 7 (10), 1083–1095.CrossRefGoogle Scholar
Robins, A. G. 1978 Plume dispersion from ground level sources in simulated atmospheric boundary layers. Atmos. Environ. 12 (5), 1033–1044.CrossRefGoogle Scholar
Sawford, B. L., Frost, C. C. & Allan, T. C. 1985 Atmospheric boundary-layer measurements of concentration statistics from isolated and multiple sources. Boundary-Layer Meteorol. 31 (3), 249–268.Google Scholar
de Silva, C. M., Philip, J., Hutchins, N. & Marusic, I. 2017 Interfaces of uniform momentum zones in turbulent boundary layers. J. Fluid Mech. 820, 451–478.Google Scholar
Smith, F. B. & Hay, J. S. 1961 The expansion of clusters of particles in the atmosphere. Q. J. R. Meteorol. Soc. 87 (371), 82–101.Google Scholar
Smits, A. J., McKeon, B. J. & Marusic, I. 2011 High-Reynolds number wall turbulence. Annu. Rev. Fluid Mech. 43, 353–375.Google Scholar
Talluru, K. M., Hernandez-Silva, C., Philip, J. & Chauhan, K. A. 2017a Measurements of scalar released from point sources in a turbulent boundary layer. Meas. Sci. Technol. 28 (5), 055801.CrossRefGoogle Scholar
Talluru, K. M., Hernandez-Silva, C., Philip, J. & Chauhan, K. A. 2017b Measurements of velocity and concentration in a high Reynolds number turbulent boundary layer. In Tenth International Symposium on Turbulence and Shear Flow Phenomena, Chicago, USA.Google Scholar
Talluru, K. M., Kulandaivelu, V., Hutchins, N. & Marusic, I. 2014 A calibration technique to correct sensor drift issues in hot-wire anemometry. Meas. Sci. Technol. 25 (10), 105304.Google Scholar
Tavoularis, S. & Corrsin, S. 1981 Experiments in nearly homogenous turbulent shear flow with a uniform mean temperature gradient. Part 1. J. Fluid Mech. 104, 311–347.Google Scholar
Taylor, G. I. 1921 Diffusion by continuous movements. Proc. Lond. Math. Soc. 2 (1), 196–212.Google Scholar
Tennekes, H. & Lumley, J. L. 1972 A First Course in Turbulence. MIT Press.Google Scholar
Townsend, A. A. 1958 Turbulent flow in a stably stratified atmosphere. J. Fluid Mech. 3 (4), 361–372.Google Scholar
Townsend, A. A. 1976 The Structure of Turbulent Shear Flow. Cambridge University Press.Google Scholar
Vanderwel, C. & Tavoularis, S. 2014 Measurements of turbulent diffusion in uniformly sheared flow. J. Fluid Mech. 754, 488–514.Google Scholar
Vanderwel, C. & Tavoularis, S. 2016 Scalar dispersion by coherent structures in uniformly sheared flow generated in a water tunnel. J. Turbul. 17 (7), 633–650.CrossRefGoogle Scholar
Weil, J. C. 2012 Atmospheric dispersion. In Handbook of Environmental Fluid Dynamics, Volume Two: Systems, Pollution Modeling and Measurements (ed. Fernando, H. J.), pp. 163–174. CRC Press.Google Scholar
Willis, G. E. & Deardorff, J. W. 1978 A laboratory study of dispersion from an elevated source within a modeled convective planetary boundary layer. Atmos. Environ. 12 (6–7), 1305–1311.Google Scholar
Yee, E. & Biltoft, C. A. 2004 Concentration fluctuation measurements in a plume dispersing through a regular array of obstacles. Boundary-Layer Meteorol. 111 (3), 363–415.Google Scholar
Yee, E., Kosteniuk, P. R., Chandler, G. M., Biltoft, C. A. & Bowers, J. F. 1993 Statistical characteristics of concentration fluctuations in dispersing plumes in the atmospheric surface layer. Boundary-Layer Meteorol. 65 (1–2), 69–109.Google Scholar