Hostname: page-component-669899f699-2mbcq Total loading time: 0 Render date: 2025-04-27T12:42:24.541Z Has data issue: false hasContentIssue false
  • English
  • Français

Matched asymptotic solutions for turbulent plumes

Published online by Cambridge University Press:  12 April 2012

Fabien Candelier  and
Olivier Vauquelin
Fabien Candelier*
Affiliation:
Aix-Marseille Univ. – Laboratoire IUSTI, UMR 6595, 5 rue Enrico Fermi, 13453 Marseille CEDEX 13, France
Olivier Vauquelin
Affiliation:
Aix-Marseille Univ. – Laboratoire IUSTI, UMR 6595, 5 rue Enrico Fermi, 13453 Marseille CEDEX 13, France
*
†Email address for correspondence: fabien.candelier@univ-amu.fr
Get access Rights & Permissions [Opens in a new window]

Abstract

Recent analytical investigations have shown that the vertical evolution of turbulent plumes variables can be derived straightforwardly from the knowledge of a single function 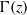(called the plume function) which is the solution of a nonlinear differential equation. This article presents matched asymptotic solutions of this equation in the cases corresponding to highly lazy or highly forced plumes. First, it is shown that, far from the source, the asymptotic expression of the plume function can be derived by means of a perturbation method based on a Padé-like approximation. The resulting outer solution is invariant under translation (with respect to the vertical coordinate) so that we are led to the classical problem concerning the location of the plume (asymptotic) virtual origin. In order to determine this virtual origin location as a function of the conditions at the source, the far-field asymptotic solution is matched to an inner expansion of the solution which is valid near the source. Comparisons between these asymptotic solutions and numerical results are finally made in order to test their validity.

JFM classification

Convection: Plumes/thermals
Type
Papers
Information
Journal of Fluid Mechanics , Volume 699 , 25 May 2012 , pp. 489 - 499
Copyright
Copyright © Cambridge University Press 2012

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

1. Baines, W. D. & Turner, J. S. 1969 Turbulent buoyant convection from a source in a confined region. J. Fluid Mech. 37, 51–80.Google Scholar
2. Carlotti, P. & Hunt, G. R. 2005 Analytical solutions for turbulent non-Boussinesq plumes. J. Fluid Mech. 538, 343–359.Google Scholar
3. Delichatsios, M. A. 1980 Strong turbulent buoyant plumes. I. Similarity. Combust. Sci. Technol. 24, 191–199.CrossRefGoogle Scholar
4. Heskestad, G. 1984 Engineering relations for fire plumes. Fire Safety. J. 7, 25–32.CrossRefGoogle Scholar
5. Hinch, E. J. 1991 Perturbation Methods. Cambridge University Press.Google Scholar
6. Hunt, G. R. & Kaye, N. G. 2001 Virtual origin correction for lazy turbulent plumes. J. Fluid Mech. 435, 377–396.CrossRefGoogle Scholar
7. Hunt, G. R. & Kaye, N. G. 2005 Lazy plumes. J. Fluid Mech. 533, 329–338.CrossRefGoogle Scholar
8. List, E. J. 1982 Turbulent jets and plumes. Annu. Rev. Fluid Mech. 14, 189.Google Scholar
9. Michaux, G. & Vauquelin, O. 2008 Solutions for turbulent buoyant plumes rising from circular sources. Phys. Fluids 20, 066601.CrossRefGoogle Scholar
10. Morton, B. R., Taylor, G. I. & Turner, J. S. 1956 Turbulent gravitational convection from maintained and instantaneous sources. Proc. R. Soc. Lond. A 234, 1–23.Google Scholar
11. Morton, B. R. 1959 Forced plumes. J. Fluid Mech. 5, 151–163.CrossRefGoogle Scholar
12. Morton, B. R. 1965 Modelling fire plumes. In 10th International Symposium on Combustion, The Combustion Institute, pp. 973–982. Elsevier.Google Scholar
13. Morton, B. R. & Middleton, J. 1973 Scale diagrams for forced plumes. J. Fluid Mech. 58, 165–176.CrossRefGoogle Scholar
14. Rooney, G. G. & Linden, P. F. 1996 Similarity considerations for non-Boussinesq plumes in an unstratified environment. J. Fluid Mech. 318, 237–250.CrossRefGoogle Scholar
15. Turner, J. S. 1969 Buoyant plumes and thermals. Annu. Rev. Fluid Mech. 1, 29.CrossRefGoogle Scholar
16. Van den Bremer, T. S. & Hunt, G. R. 2010 Universal solutions for Boussinesq and non-Boussinesq plumes. J. Fluid Mech. 644, 165–192.Google Scholar
17. Woods, A. W. 2010 Turbulent plumes in nature. Annu. Rev. Fluid Mech. 42, 391–412.CrossRefGoogle Scholar