Hostname: page-component-586b7cd67f-2brh9 Total loading time: 0 Render date: 2024-11-26T18:14:11.577Z Has data issue: false hasContentIssue false
  • English
  • Français

Mean and turbulence dynamics in unsteady Ekman boundary layers

Published online by Cambridge University Press:  07 March 2017

Mostafa Momen Open the ORCID record for Mostafa Momen [Opens in a new window]  and
Elie Bou-Zeid
Mostafa Momen*
Affiliation:
Department of Civil and Environmental Engineering, Princeton University, Princeton, NJ 08544, USA
Elie Bou-Zeid*
Affiliation:
Department of Civil and Environmental Engineering, Princeton University, Princeton, NJ 08544, USA
*
†Email addresses for correspondence: mostafa@princeton.edu, ebouzeid@princeton.edu
†Email addresses for correspondence: mostafa@princeton.edu, ebouzeid@princeton.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

Unsteady pressure gradients in turbulent flows not only influence the mean, but also affect the higher statistical moments of turbulence. In these flows, it is important to understand if and when turbulence is in quasi-equilibrium with the mean in order to better capture the dynamics and develop effective closure models. Therefore, this study aims to elucidate how turbulence decays or develops relative to a time-varying mean flow, and how the turbulent kinetic energy (TKE) production, transport and dissipation respond to changes in the imposed pressure forcing. The focus is on the neutral unsteady Ekman boundary layer, where pressure-gradient, Coriolis and turbulent friction forces interact, and the analyses are based on a suite of large-eddy simulations with unsteady pressure forcing. 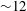The results indicate that the dynamics is primarily controlled by the relative magnitudes of three time scales: the inertial time scale (characterized by Coriolis frequency ${\sim}12$ hours at mid-latitudes), the turbulent time scale (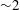${\sim}2$ hours for the largest eddies in the present simulations) and the forcing variability time scale (which is varied to reflect different (sub)meso to synoptic scale dynamics). When the forcing time scale is comparable to the turbulence time scale, the quasi-equilibrium condition becomes invalid due to highly complex interactions between the mean and turbulence, the velocity profiles manifestly depart from the log-law and the normalized TKE budget terms vary strongly in time. However, for longer, and surprisingly for shorter, forcing times, quasi-equilibrium is reasonably maintained. The analyses elucidate the physical mechanisms that trigger these dynamics, and investigate the implications on turbulence closure models.

JFM classification

Geophysical and Geological Flows: Atmospheric flows Turbulent Flows: Turbulence modelling Turbulent Flows: Turbulent boundary layers
Type
Papers
Information
Journal of Fluid Mechanics , Volume 816 , 10 April 2017 , pp. 209 - 242
Check for updates
Copyright
© 2017 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

‡

Present address: E414-CEE-EQuad, Princeton, NJ 08544, USA.

References

Bou-Zeid, E., Meneveau, C. & Parlange, M. 2005 A scale-dependent Lagrangian dynamic model for large eddy simulation of complex turbulent flows. Phys. Fluids 17 (2), 025105.Google Scholar
Bou-Zeid, E., Overney, J., Rogers, B. D. & Parlange, M. B. 2009 The effects of building representation and clustering in large-eddy simulations of flows in urban canopies. Boundary-Layer Meteorol. 132 (3), 415–436.Google Scholar
Canuto, V. M. & Cheng, Y. 1997 Determination of the Smagorinsky–Lilly constant Cs. Phys. Fluids 9 (5), 1368–1378.CrossRefGoogle Scholar
Catalano, F. & Moeng, C. H. 2010 Large-eddy simulation of the daytime boundary layer in an idealized valley using the weather research and forecasting numerical model. Boundary-Layer Meteorol. 137, 49–75.CrossRefGoogle Scholar
Chollet, J. P. & Lesieur, M. 1981 Parametrization of small scales of three dimensional isotropic turbulence utilizing spectral closures. J. Atmos. Sci. 38, 2747–2757.Google Scholar
Drobinski, P. & Foster, R. C. 2003 On the origin of near-surface streaks in the neutrally-stratified planetary boundary layer. Boundary-Layer Meteorol. 108, 247–256.CrossRefGoogle Scholar
Fritts, D. C. & Nastrom, G. D. 1992 Sources of mesoscale variability of gravity waves. II – Frontal, convective, and jet stream excitation. J. Atmos. Sci. 49 (2), 111–112.Google Scholar
Gayen, B., Sarkar, S. & Taylor, J. R. 2010 Large eddy simulation of a stratified boundary layer under an oscillatory current. J. Fluid Mech. 643, 233–266.Google Scholar
Harun, Z., Monty, J. P., Mathis, R. & Marusic, I. 2013 Pressure gradient effects on the large-scale structure of turbulent boundary layers. J. Fluid Mech. 715, 477–498.CrossRefGoogle Scholar
Hino, M., Kashiwayanagi, M., Nakayama, A. & Hara, T. 1983 Experiments on the turbulence statistics and the structure of a reciprocating oscillatory flow. J. Fluid Mech. 131, 363–400.Google Scholar
Högström, U., Hunt, J. C. R. & Smedman, A. S. 2002 Theory and measurements for turbulence spectra and variances in the atmospheric neutral surface layer. Boundary-Layer Meteorol. 103, 101–124.Google Scholar
Hsu, B. C., Lu, X. & Kwan, M. 2000 LES and RANS studies of oscillating flows over flat plate. J. Engng Mech. 126 (February), 186–193.Google Scholar
Jensen, B. L., Sumer, B. M. & Fredsoe, J. 1989 Turbulent oscillatory boundary layers at high Reynolds numbers. J. Fluid Mech. 206, 265–297.CrossRefGoogle Scholar
Kannepalli, C. & Piomelli, U. 2000 Large-eddy simulation of a three-dimensional shear-driven turbulent boundary layer. J. Fluid Mech. 423, 175–203.CrossRefGoogle Scholar
Kirkil, G., Mirocha, J., Bou-Zeid, E., Chow, F. K. & Kosović, B. 2012 Implementation and evaluation of dynamic subfilter-scale stress models for large-eddy simulation using WRF. Mon. Weath. Rev. 140 (1), 266–284.Google Scholar
Knaepen, B., Debliquy, O. & Carati, D. 2002 Subgrid-scale energy and pseudo pressure in large-eddy simulation. Phys. Fluids 14, 4235–4241.Google Scholar
Kosovic, B. 1997 Subgrid-scale modelling for the large-eddy simulation of high-Reynolds-number boundary layers. J. Fluid Mech. 336, 151–182.Google Scholar
Kosovic, B. & Curry, J. A. 2000 A large eddy simulation study of a quasi-steady, stably stratified atmospheric boundary layer. J. Atmos. Sci. 57, 1052–1068.Google Scholar
Li, Q., Bou-Zeid, E. & Anderson, W. 2016 The impact and treatment of the Gibbs phenomenon in immersed boundary method simulations of momentum and scalar transport. J. Comput. Phys. 310, 237–251.Google Scholar
Lodahl, C. R., Sumer, B. M. & Fredsøe, J. 1998 Turbulent combined oscillatory flow and current in a pipe. J. Fluid Mech. 373, 313–348.CrossRefGoogle Scholar
Lohmann, I. P., Fredsøe, J., Sumer, B. M. & Christensen, E. D. 2006 Large eddy simulation of the ventilated wave boundary layer. J. Geophys. Res. 111 (C6), C06036.Google Scholar
Madabhushi, R. K. & Vanka, S. P. 1991 Large eddy simulation of turbulence-driven secondary flow in a square duct. Phys. Fluids 3, 2734–2745.Google Scholar
Mankbadi, R. R. & Liu, J. T. C. 1992 Near-wall response in turbulent shear flows subjected to imposed unsteadiness. J. Fluid Mech. 238, 55–71.Google Scholar
Mann, J. 1994 The spatial structure of neutral atmospheric surface-layer turbulence. J. Fluid Mech. 273, 141–168.Google Scholar
Meneveau, C. & Katz, J. 2000 Scale-invariance and turbulence models for large-eddy simulation. Annu. Rev. Fluid Mech. 32, 1–32.Google Scholar
Mirocha, J., Kirkil, G., Bou-Zeid, E., Chow, F. K. & Kosović, B. 2013 Transition and equilibration of neutral atmospheric boundary layer flow in one-way nested large-eddy simulations using the weather research and forecasting model. Mon. Weath. Rev. 141 (3), 918–940.Google Scholar
Moeng, C.-H. 1986 Large-eddy simulation of a stratus-topped boundary layer. Part I: structure and budgets. J. Atmos. Sci. 43 (23), 2886–2900.Google Scholar
Momen, M. & Bou-Zeid, E. 2016 Large eddy simulations and damped-oscillator models of the unsteady Ekman boundary layer. J. Atmos. Sci. 73 (1), 25–40.Google Scholar
Ohfuchi, W., Nakamura, H., Yoshioka, M., Enomoto, T., Takaya, K., Peng, X., Yamane, S., Nishimura, T., Kurihara, Y., Ninomiya, K. et al. 2004 10-km mesh meso-scale resolving simulations of the global atmosphere on the earth simulator: preliminary outcomes of AFES (AGCM for the earth simulator). J. Earth Simulator 1 (April), 8–34.Google Scholar
Pope, S. B. 2000 Turbulent Flows, 1st edn. Cambridge University Press.CrossRefGoogle Scholar
Radhakrishnan, S. & Piomelli, U. 2008 Large-eddy simulation of oscillating boundary layers: model comparison and validation. J. Geophys. Res. Ocean 113 (2), 1–14.Google Scholar
Salesky, S. T. & Chamecki, M. 2012 A similarity model of subfilter-scale energy for large-eddy simulations of the atmospheric boundary layer. Boundary-Layer Meteorol. 145, 69–91.Google Scholar
Salon, S., Armenio, V. & Crise, A. 2007 A numerical investigation of the Stokes boundary layer in the turbulent regime. J. Fluid Mech. 570, 253–296.Google Scholar
Sarpkaya, T. 1993 Coherent structures in oscillatory boundary layers. J. Fluid Mech. 253, 105–140.Google Scholar
Scotti, A. & Piomelli, U. 2001 Numerical simulation of pulsating turbulent channel flow. Phys. Fluids 13 (5), 1367–1384.CrossRefGoogle Scholar
Shah, S. K. & Bou-Zeid, E. 2014 Direct numerical simulations of turbulent Ekman layers with increasing static stability: modifications to the bulk structure and second-order statistics. J. Fluid Mech. 760, 494–539.Google Scholar
Spalart, P. R. & Baldwin, B. S. 1990 Simulation of turbulent, oscillating boundary layer. Turbul. Shear Flows 6 (1), 417–440.Google Scholar
Sugita, M. & Brutsaert, W. 1990 Wind velocity measurements in the neutral boundary layer above hilly prairie. J. Geophys. Res. 95, 7617–7624.Google Scholar
Tennekes, H. & Lumley, J. 1972 A First Course in Turbulence, MIT Press.Google Scholar
Supplementary material: File

Momen and Bou-Zeid supplementary material

Momen and Bou-Zeid supplementary material 1

Download Momen and Bou-Zeid supplementary material(File)
File 7.8 MB