Published online by Cambridge University Press: 10 July 2015
This work reports an experimental investigation of the dispersion of a low-diffusive dye within a homogeneous swarm of high-Reynolds-number rising bubbles at gas volume fractions  ${\it\alpha}$ ranging from 1 % to 13 %. The capture and transport of dye within bubble wakes is found to be negligible and the mixing turns out to result from the bubble-induced turbulence. It is described well by a regular diffusion process. The diffusion coefficient corresponding to the vertical direction is larger than that corresponding to the horizontal direction, owing to the larger intensity of the liquid fluctuations in the vertical direction. Two regimes of diffusion have been identified. At low gas volume fraction, the diffusion time scale is given by the correlation time of the bubble-induced turbulence and the diffusion coefficients increase roughly as
${\it\alpha}$ ranging from 1 % to 13 %. The capture and transport of dye within bubble wakes is found to be negligible and the mixing turns out to result from the bubble-induced turbulence. It is described well by a regular diffusion process. The diffusion coefficient corresponding to the vertical direction is larger than that corresponding to the horizontal direction, owing to the larger intensity of the liquid fluctuations in the vertical direction. Two regimes of diffusion have been identified. At low gas volume fraction, the diffusion time scale is given by the correlation time of the bubble-induced turbulence and the diffusion coefficients increase roughly as 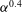 ${\it\alpha}^{0.4}$. At large gas volume fraction, the diffusion time scale is imposed by the time interval between two bubbles and the diffusion coefficients become almost independent of
${\it\alpha}^{0.4}$. At large gas volume fraction, the diffusion time scale is imposed by the time interval between two bubbles and the diffusion coefficients become almost independent of  ${\it\alpha}$. The transition between the two regimes occurs sooner in the horizontal direction (
${\it\alpha}$. The transition between the two regimes occurs sooner in the horizontal direction (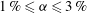 $1\,\%\leqslant {\it\alpha}\leqslant 3\,\%$) than in the vertical direction (
$1\,\%\leqslant {\it\alpha}\leqslant 3\,\%$) than in the vertical direction (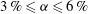 $3\,\%\leqslant {\it\alpha}\leqslant 6\,\%$). Physical models based on the hydrodynamic properties of the bubble swarm are introduced and guidelines for practical applications are suggested.
$3\,\%\leqslant {\it\alpha}\leqslant 6\,\%$). Physical models based on the hydrodynamic properties of the bubble swarm are introduced and guidelines for practical applications are suggested.
To send this article to your Kindle, first ensure no-reply@cambridge.org is added to your Approved Personal Document E-mail List under your Personal Document Settings on the Manage Your Content and Devices page of your Amazon account. Then enter the ‘name’ part of your Kindle email address below. Find out more about sending to your Kindle. Find out more about saving to your Kindle.
Note you can select to save to either the @free.kindle.com or @kindle.com variations. ‘@free.kindle.com’ emails are free but can only be saved to your device when it is connected to wi-fi. ‘@kindle.com’ emails can be delivered even when you are not connected to wi-fi, but note that service fees apply.
Find out more about the Kindle Personal Document Service.
To save this article to your Dropbox account, please select one or more formats and confirm that you agree to abide by our usage policies. If this is the first time you used this feature, you will be asked to authorise Cambridge Core to connect with your Dropbox account. Find out more about saving content to Dropbox.
To save this article to your Google Drive account, please select one or more formats and confirm that you agree to abide by our usage policies. If this is the first time you used this feature, you will be asked to authorise Cambridge Core to connect with your Google Drive account. Find out more about saving content to Google Drive.