Article contents
Mixing of the fluid phase in slowly sheared particle suspensions of cylinders
Published online by Cambridge University Press: 06 April 2017
Abstract
We introduce a finite element model for neutrally buoyant particle suspensions of cylinders at zero Reynolds number and infinite Péclet number in the purely hydrodynamic limit, which allows us to access a high-accuracy fluid velocity field at any time during the simulation. We use the diffusive strip method to characterize the development of the concentration field in the fluid phase of sheared suspensions from initial thin filaments, and characterize the structures that form with their fractal dimension. We find that the growth of the fractal dimension of the filaments scales with the increase of mean square displacement in the fluid phase. Further, we measure the concentration distribution of tracers in the fluid phase, as well as the shear-induced self-diffusion coefficient in both the solid phase and the fluid phase. We demonstrate that the shear-induced self-diffusion coefficient is slightly larger in the fluid phase at infinite Péclet number. Finally, we investigate enhanced mass diffusivity in the fluid phase by systematic measurements of the shear-induced self-diffusion coefficient in the fluid phase for a wide range of fluid tracer Péclet numbers. We find that the functional dependence 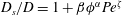 $D_{s}/D=1+\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D719}^{\unicode[STIX]{x1D6FC}}Pe^{\unicode[STIX]{x1D701}}$ (where
$D_{s}/D=1+\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D719}^{\unicode[STIX]{x1D6FC}}Pe^{\unicode[STIX]{x1D701}}$ (where 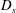 $D_{s}$ is the shear-induced self-diffusion coefficient,
$D_{s}$ is the shear-induced self-diffusion coefficient, 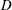 $D$ is the molecular diffusivity and
$D$ is the molecular diffusivity and 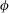 $\unicode[STIX]{x1D719}$ is the particle volume fraction) fits the observations fairly well. We measure the constants
$\unicode[STIX]{x1D719}$ is the particle volume fraction) fits the observations fairly well. We measure the constants 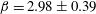 $\unicode[STIX]{x1D6FD}=2.98\pm 0.39$ ,
$\unicode[STIX]{x1D6FD}=2.98\pm 0.39$ , 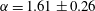 $\unicode[STIX]{x1D6FC}=1.61\pm 0.26$ and
$\unicode[STIX]{x1D6FC}=1.61\pm 0.26$ and 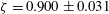 $\unicode[STIX]{x1D701}=0.900\pm 0.031$ .
$\unicode[STIX]{x1D701}=0.900\pm 0.031$ .
Information
- Type
- Papers
- Information
- Copyright
- © 2017 Cambridge University Press
References
- 3
- Cited by


