Hostname: page-component-586b7cd67f-t7czq Total loading time: 0 Render date: 2024-11-29T03:34:52.882Z Has data issue: false hasContentIssue false
  • English
  • Français

Near-wall nanovelocimetry based on total internal reflection fluorescence with continuous tracking

Published online by Cambridge University Press:  02 February 2015

Zhenzhen Li ,
Loïc D’eramo ,
Choongyeop Lee ,
Fabrice Monti ,
Marc Yonger ,
Patrick Tabeling ,
Benjamin Chollet ,
Bruno Bresson  and
Yvette Tran
Zhenzhen Li
Affiliation:
MMN, CNRS, ESPCI Paris-Tech, 10 rue Vauquelin, 75005 Paris, France
Loïc D’eramo*
Affiliation:
MMN, CNRS, ESPCI Paris-Tech, 10 rue Vauquelin, 75005 Paris, France
Choongyeop Lee
Affiliation:
MMN, CNRS, ESPCI Paris-Tech, 10 rue Vauquelin, 75005 Paris, France
Fabrice Monti
Affiliation:
MMN, CNRS, ESPCI Paris-Tech, 10 rue Vauquelin, 75005 Paris, France
Marc Yonger
Affiliation:
MMN, CNRS, ESPCI Paris-Tech, 10 rue Vauquelin, 75005 Paris, France
Patrick Tabeling
Affiliation:
MMN, CNRS, ESPCI Paris-Tech, 10 rue Vauquelin, 75005 Paris, France
Benjamin Chollet
Affiliation:
PPMD-SIMM, CNRS, ESPCI Paris-Tech, 10 rue Vauquelin, 75005 Paris, France
Bruno Bresson
Affiliation:
PPMD-SIMM, CNRS, ESPCI Paris-Tech, 10 rue Vauquelin, 75005 Paris, France
Yvette Tran
Affiliation:
PPMD-SIMM, CNRS, ESPCI Paris-Tech, 10 rue Vauquelin, 75005 Paris, France
*
†Email address for correspondence: loic.deramo@espci.fr
Get access Rights & Permissions [Opens in a new window]

Abstract

The goal of this work is to make progress in the domain of near-wall velocimetry. The technique we use is based on the tracking of nanoparticles in an evanescent field, close to a wall, a technique called TIRF (total internal reflection fluorescence)-based velocimetry. The particles are filmed continuously, with no time gap between two frames, so that no information on their trajectories is lost. A number of biases affect the measurements: Brownian motion, heterogeneities induced by the walls, statistical biases, photobleaching, polydispersivity and limited depth of field. Their impacts are quantified by carrying out Langevin stochastic simulations, in a way similar to Guasto & Breuer (Exp. Fluids, vol. 47, 2009, pp. 1059–1066). By using parameters calibrated separately or known, we obtain satisfactory agreement between experiments and simulations, concerning the intensity density distributions, velocity fluctuation distributions and the slopes of the linear velocity profiles. Slip lengths measurements, taken as benchmarks for analysing the performances of the technique, are carried out by extrapolating the corrected velocity profiles down to the origin along with determining the wall position with an unprecedented accuracy. For hydrophilic surfaces, we obtain 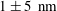$1\pm 5~\text{nm}$ for the slip length in sucrose solutions and 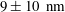$9\pm 10~\text{nm}$ in water, and for hydrophobic surfaces, 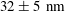$32\pm 5~\text{nm}$ for sucrose solutions and $55\pm 9~\text{nm}$ for water. The errors (based on 95 % confidence intervals) are significantly smaller than the state of the art, but more importantly, the method demonstrates for the first time a capacity to measure slippage with a satisfactory accuracy, while providing a local information on the flow structure with a nanometric spatial precision and velocity errors of a few per cent. Our study confirms the discrepancy already pointed out in the literature between numerical and experimental slip length estimates. With the progress conveyed by the present work, TIRF-based technique with continuous tracking can be considered as a quantitative method for investigating flow properties close to walls, providing both global and local information on the flow.

JFM classification

Micro-/Nano-fluid dynamics: Micro-/Nano-fluid dynamics Non-Newtonian Flows: Non-Newtonian Flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 766 , 10 March 2015 , pp. 147 - 171
Check for updates
Copyright
© 2015 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bartolo, D., Degré, G., Nghe, P. & Studer, V. 2008 Microfluidic stickers. Lab on a Chip 8 (2), 274–279.Google Scholar
Bocquet, L. & Barrat, J.-L. 2007 Flow boundary conditions from nano- to micro-scales. Soft Matt. 3 (6), 685–693.Google Scholar
Bocquet, L. & Charlaix, E. 2010 Nanofluidics, from bulk to interfaces. Chem. Soc. Rev. 39 (3), 1073–1095.Google Scholar
Bonneau, S., Dahan, M. & Cohen, L. D. 2005 Single quantum dot tracking based on perceptual grouping using minimal paths in a spatiotemporal volume. IEEE Trans. Image Process. 14 (9), 1384–1395.Google Scholar
Bouzigues, C. I., Tabeling, P. & Bocquet, L. 2008 Nanofluidics in the debye layer at hydrophilic and hydrophobic surfaces. Phys. Rev. Lett. 101 (11), 114503.Google Scholar
Brazhnik, P. K., Freed, K. F. & Tang, H. 1994 Polymer melt near a solid wall. J. Chem. Phys. 101 (10), 9143–9154.Google Scholar
Briceño, M. I. & Joseph, D. D. 2003 Self-lubricated transport of aqueous foams in horizontal conduits. Intl J. Multiphase Flow 29 (12), 1817–1831.Google Scholar
Brochard, F. & De Gennes, P. G. 1992 Shear-dependent slippage at a polymer/solid interface. Langmuir 8 (12), 3033–3037.Google Scholar
Cevheri, N. & Yoda, M. 2014 Electrokinetically driven reversible banding of colloidal particles near the wall. Lab on a Chip 14, 1391–1394.Google Scholar
Choi, C.-H., Westin, K. J. A. & Breuer, K. S. 2003 Apparent slip flows in hydrophilic and hydrophobic microchannels. Phys. Fluids 15 (10), 2897–2902.CrossRefGoogle Scholar
Cottin-Bizonne, C., Cross, B., Steinberger, A. & Charlaix, E. 2005 Boundary slip on smooth hydrophobic surfaces: intrinsic effects and possible artifacts. Phys. Rev. Lett. 94 (5), 056102.Google Scholar
de Gennes, P. G. 1980 Conformations of polymers attached to an interface. Macromolecules 13 (5), 1069–1075.Google Scholar
De Gennes, P. G. 1981 Polymer solutions near an interface. adsorption and depletion layers. Macromolecules 14 (6), 1637–1644.Google Scholar
Ermak, D. L. & McCammon, J. A. 1978 Brownian dynamics with hydrodynamic interactions. J. Chem. Phys. 69 (4), 1352–1360.Google Scholar
Guasto, J. S. & Breuer, K. S. 2009 High-speed quantum dot tracking and velocimetry using evanescent wave illumination. Exp. Fluids 47 (6), 1059–1066.Google Scholar
Guasto, J. S., Huang, P. & Breuer, K. S. 2006 Statistical particle tracking velocimetry using molecular and quantum dot tracer particles. Exp. Fluids 41 (6), 869–880.Google Scholar
Hu, G. & Li, D. 2007 Multiscale phenomena in microfluidics and nanofluidics. Chem. Engng Sci. 62 (13), 3443–3454.Google Scholar
Huang, P. & Breuer, K. S. 2007 Direct measurement of anisotropic near-wall hindered diffusion using total internal reflection velocimetry. Phys. Rev. E 76 (4), 046307.Google Scholar
Huang, P., Guasto, J. S. & Breuer, K. S. 2006 Direct measurement of slip velocities using three-dimensional total internal reflection velocimetry. J. Fluid Mech. 566, 447–464.Google Scholar
Huang, P., Guasto, J. S. & Breuer, K. S. 2009 The effects of hindered mobility and depletion of particles in near-wall shear flows and the implications for nanovelocimetry. J. Fluid Mech. 637, 241–265.Google Scholar
Jin, S., Huang, P., Park, J., Yoo, J. Y. & Breuer, K. S. 2004 Near-surface velocimetry using evanescent wave illumination. Exp. Fluids 37 (6), 825–833.CrossRefGoogle Scholar
Joly, L., Ybert, C. & Bocquet, L. 2006 Probing the nanohydrodynamics at liquid–solid interfaces using thermal motion. Phys. Rev. Lett. 96, 046101.Google Scholar
Joseph, P. & Tabeling, P. 2005 Direct measurement of the apparent slip length. Phys. Rev. E 71 (3), 035303.Google Scholar
Kazoe, Y., Iseki, K., Mawatari, K. & Kitamori, T. 2013 Evanescent wave-based particle tracking velocimetry for nanochannel flows. Analyt. Chem. 85 (22), 10780–10786.Google Scholar
Kimura, Y. & Okada, K. 1989 Lubricating properties of oil-in-water emulsions. Tribol. Trans. 32 (4), 524–532.Google Scholar
Koch, D. L. 1989 On hydrodynamic diffusion and drift in sheared suspensions. Phys. Fluids A 1 (10), 1742–1745.Google Scholar
Li, H., Sadr, R. & Yoda, M. 2006 Multilayer nano-particle image velocimetry. Exp. Fluids 41 (2), 185–194.Google Scholar
Li, H. F. & Yoda, M. 2008 Multilayer nano-particle image velocimetry (MnPIV) in microscale poiseuille flows. Meas. Sci. Technol. 19 (7), 075402.Google Scholar
Li, H. & Yoda, M. 2010 An experimental study of slip considering the effects of non-uniform colloidal tracer distributions. J. Fluid Mech. 662, 269–287.Google Scholar
McGovern, M. E., Kallury, K. M. R. & Thompson, M. 1994 Role of solvent on the silanization of glass with octadecyltrichlorosilane. Langmuir 10 (10), 3607–3614.Google Scholar
Meeker, S. P., Bonnecaze, R. T. & Cloitre, M. 2004 Slip and flow in soft particle pastes. Phys. Rev. Lett. 92 (19), 198302.Google Scholar
Meinhart, C. D., Wereley, S. T. & Santiago, J. G. 1999 PIV measurements of a microchannel flow. Exp. Fluids 27 (5), 414–419.Google Scholar
Mijatovic, D., Eijkel, J. C. T. & van den Berg, A. 2005 Technologies for nanofluidic systems: top-down versus bottom-up – a review. Lab on a Chip 5 (5), 492–500.Google Scholar
Murat, M. & Grest, G. S. 1989 Structure of a grafted polymer brush: a molecular dynamics simulation. Macromolecules 22 (10), 4054–4059.Google Scholar
Oberholzer, M. R., Wagner, N. J. & Lenhoff, A. M. 1997 Grand canonical brownian dynamics simulation of colloidal adsorption. J. Chem. Phys. 107 (21), 9157–9167.Google Scholar
Sadr, R., Hohenegger, C., Li, H., Mucha, P. J. & Yoda, M. 2007 Diffusion-induced bias in near-wall velocimetry. J. Fluid Mech. 577, 443–456.Google Scholar
Sadr, R., Li, H. & Yoda, M. 2005 Impact of hindered Brownian diffusion on the accuracy of particle-image velocimetry using evanescent-wave illumination. Exp. Fluids 38 (1), 90–98.Google Scholar
Sadr, R., Yoda, M., Zheng, Z. & Conlisk, A. T. 2004 An experimental study of electro-osmotic flow in rectangular microchannels. J. Fluid Mech. 506, 357–367.Google Scholar
Santiago, J. G., Wereley, S. T., Meinhart, C. D., Beebe, D. J. & Adrian, R. J. 1998 A particle image velocimetry system for microfluidics. Exp. Fluids 25 (4), 316–319.Google Scholar
Schmid, S. R. & Wilson, W. R. D. 1995 Lubrication of aluminum rolling by oil-in-water emulsions. Tribol. Trans. 38 (2), 452–458.Google Scholar
Selvin, P. R. & Ha, T. 2008 Single-Molecule Techniques: A Laboratory Manual. Cold Spring Harbor Laboratory Press.Google Scholar
Sessoms, D. A., Bischofberger, I., Cipelletti, L. & Trappe, V. 2009 Multiple dynamic regimes in concentrated microgel systems. Phil. Trans. R. Soc. A 367 (1909), 5013–5032.Google Scholar
Song, L., Hennink, E. J., Young, I. T. & Tanke, H. J. 1995 Photobleaching kinetics of fluorescein in quantitative fluorescence microscopy. Biophys. J. 68 (6), 2588–2600.Google Scholar
Song, L., van Gijlswijk, R. P. M., Young, I. T. & Tanke, H. J. 1997 Influence of fluorochrome labeling density on the photobleaching kinetics of fluorescein in microscopy. Cytometry 27 (3), 213–223.Google Scholar
Sparreboom, W., van den Berg, A. & Eijkel, J. C. T. 2009 Principles and applications of nanofluidic transport. Nat. Nanotechnol. 4 (11), 713–720.Google Scholar
Tretheway, D. C. & Meinhart, C. D. 2002 Apparent fluid slip at hydrophobic microchannel walls. Phys. Fluids 14 (3), L9–L12.Google Scholar
Vincent, B. 1990 The calculation of depletion layer thickness as a function of bulk polymer concentration. Colloids Surf. 50, 241–249.Google Scholar
Vinogradova, O. I., Koynov, K., Best, A. & Feuillebois, F. 2009 Direct measurements of hydrophobic slippage using double-focus fluorescence cross-correlation. Phys. Rev. Lett. 102, 118302.Google Scholar
Zettner, C. & Yoda, M. 2003 Particle velocity field measurements in a near-wall flow using evanescent wave illumination. Exp. Fluids 34 (1), 115–121.Google Scholar
Zheng, X., Kong, G.-P. & Silber-Li, Z.-H. 2013 The influence of nano-particle tracers on the slip length measurements by microPTV. Acta Mechanica Sin. 29 (3), 411–419.Google Scholar