Hostname: page-component-78c5997874-94fs2 Total loading time: 0 Render date: 2024-10-31T23:38:47.423Z Has data issue: false hasContentIssue false
  • English
  • Français

Non-geostrophic instabilities of an equilibrium baroclinic state

Published online by Cambridge University Press:  14 October 2013

Alexandre B. Pieri ,
F. S. Godeferd ,
C. Cambon  and
A. Salhi
Alexandre B. Pieri
Affiliation:
Laboratoire de Mécanique des Fluides et d’Acoustique, École Centrale de Lyon, Université de Lyon, France
F. S. Godeferd*
Affiliation:
Laboratoire de Mécanique des Fluides et d’Acoustique, École Centrale de Lyon, Université de Lyon, France
C. Cambon
Affiliation:
Laboratoire de Mécanique des Fluides et d’Acoustique, École Centrale de Lyon, Université de Lyon, France
A. Salhi
Affiliation:
Département de Physique, Faculté des Sciences de Tunis, Université de Tunis El Manar, 1060 Tunis, Tunisia
*
†Email address for correspondence: Fabien.Godeferd@ec-lyon.fr
Get access Rights & Permissions [Opens in a new window]

Abstract

We consider non-geostrophic homogeneous baroclinic turbulence without solid boundaries, and we focus on its energetics and dynamics. The homogeneous turbulent flow is therefore submitted to both uniform vertical shear 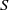$S$ and stable vertical stratification, parametrized by the Brunt–Väisälä frequency $N$, and placed in a rotating frame with Coriolis frequency 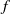$f$. Direct numerical simulations show that the threshold of baroclinic instability growth depends mostly on two dimensionless numbers, the gradient Richardson number 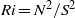$\mathit{Ri}= {N}^{2} / {S}^{2} $ and the Rossby number 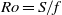$\mathit{Ro}= S/ f$, whereas linear theory predicts a threshold that depends only on 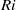$\mathit{Ri}$. At high Rossby numbers the nonlinear limit is found to be 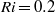$\mathit{Ri}= 0. 2$, while in the limit of low 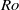$\mathit{Ro}$ the linear stability bound 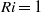$\mathit{Ri}= 1$ is recovered. We also express the stability results in terms of background potential vorticity, which is an important quantity in baroclinic flows. We show that the linear symmetric instability occurs from the presence of negative background potential vorticity. The possibility of simultaneous existence of symmetric and baroclinic instabilities is also investigated. The dominance of symmetric instability over baroclinic instability for 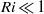$\mathit{Ri}\ll 1$ is confirmed by our direct numerical simulations, and we provide an improved understanding of the dynamics of the flow by exploring the details of energy transfers for moderate Richardson numbers.

JFM classification

Geophysical and Geological Flows: Baroclinic flows Turbulent Flows: Turbulence simulation
Type
Papers
Information
Journal of Fluid Mechanics , Volume 734 , 10 November 2013 , pp. 535 - 566
Copyright
©2013 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Andrews, D. G., Holton, J. R. & Leovy, C. B. 1987 Middle Atmosphere Dynamics, vol. 40, Academic.Google Scholar
Batchelor, G. K. 1954 Heat convection and buoyancy effects in fluids. Q. J. R. Meteorol. Soc. 80 (345), 339–358.Google Scholar
Bennetts, D. A. & Hoskins, B. J. 1979 Conditional symmetric instability: a possible explanation for frontal rainbands. Q. J. R. Meteorol. Soc. 105 (446), 945–962.Google Scholar
Bouchut, F., Ribstein, B. & Zeitlin, V. 2011 Inertial, barotropic, and baroclinic instabilities of the Bickley jet in two-layer rotating shallow water model. Phys. Fluids 23 (12), 126601.Google Scholar
Canuto, C., Hussaini, M. Y., Quarteroni, A. & Zang, T. A. 2007 Spectral Methods: Evolution to Complex Geometries and Applications to Fluid Dynamics. Springer.Google Scholar
Charney, J. G. 1947 The dynamics of long waves in a baroclinic westerly current. J. Meteorol. 4 (5), 135–162.Google Scholar
Charney, J. G. & Drazin, P. G. 1961 Propagation of planetary-scale disturbances from the lower into the upper atmosphere. J. Geophys. Res. 66 (1), 83–109.Google Scholar
Charney, J. G. & Stern, M. E. 1962 On the stability of internal baroclinic jets in a rotating atmosphere. J. Atmos. Sci. 19, 159–172.Google Scholar
Chavanis, P. H. & Dubrulle, B. 2006 Statistical mechanics of the shallow-water system with an a priori potential vorticity distribution. C. R. Phys. 7 (3), 422–432.Google Scholar
Coleman, G. N., Kim, J. & Spalart, P. R. 2000 A numerical study of strained three-dimensional wall-bounded turbulence. J. Fluid Mech. 416, 75–116.Google Scholar
Conrath, B. J., Gierasch, P. J. & Nath, N. 1981 Stability of zonal flows on Jupiter. Icarus 48 (2), 256–282.Google Scholar
Davies, H. C. & Bishop, C. H. 1994 Eady edge waves and rapid development. J. Atmos. Sci. 51 (13), 1930–1946.Google Scholar
Delorme, P. 1985 Simulation numérique de turbulence homogène compressible avec ou sans cisaillement imposé. PhD Thesis, University of Poitiers, France.Google Scholar
Donivan, F. F. & Carr, T. D. 1969 Jupiter’s decametric rotation period. Astrophys. J. 157, L65–L68.Google Scholar
Drazin, P. G. & Reid, W. H. 2004 Hydrodynamic Stability. Cambridge University Press.Google Scholar
Dubrulle, B. & Nazarenko, S. 1994 On scaling laws for the transition to turbulence in uniform-shear flows. Europhys. Lett. 27, 129.Google Scholar
Eady, E. T. 1949 Long waves and cyclone waves. Tellus 1, 33–52.Google Scholar
Egger, J. 2009 Baroclinic instability in the Eady model: interpretations. J. Atmos. Sci. 66, 1856–1859.Google Scholar
Ertel, H. 1942 Ein neuer hydrodynamischer Wirbelsatz. Meteor. Z. 59 (9), 271–281.Google Scholar
Farrell, B. F. 1982 The initial growth of disturbances in a baroclinic flow. J. Atmos. Sci. 39, (08).Google Scholar
Farrell, B. F. 1984 Modal and non-modal baroclinic waves. J. Atmos. Sci. 41 (4), 668–673.Google Scholar
Flasar, F. M., Kunde, V. G., Achterberg, R. K., Conrath, B. J., Simon-Miller, A. A., Nixon, C. A., Gierasch, P. J., Romani, P. N., Bézard, B. & Irwin, P. 2004 An intense stratospheric jet on Jupiter. Nature 427 (6970), 132–135.Google Scholar
Gierasch, P. J., Ingersoll, A. P. & Pollard, D. 1979 Baroclinic instabilities in Jupiter’s zonal flow. Icarus 40 (2), 205–212.Google Scholar
Haine, T. W. N. & Marshall, J. 1998 Gravitational, symmetric, and baroclinic instability of the ocean mixed layer. J. Phys. Oceanogr. 28 (4), 634–658.Google Scholar
Hedin, A. E., Fleming, E. L., Manson, A. H., Schmidlin, F. J., Avery, S. K., Clark, R. R., Franke, S. J., Fraser, G. J., Tsuda, T. & Vial, F. 1996 Empirical wind model for the upper, middle and lower atmosphere. J. Atmos. Terr. Phys. 58 (13), 1421–1447.Google Scholar
Hill, E. L. 1951 Hamilton’s principle and the conservation theorems of mathematical physics. Rev. Mod. Phys. 23 (3), 253–260.Google Scholar
Holton, J. R. 2004 An Introduction to Dynamic Meteorology, vol. 1, Academic.Google Scholar
Hoskins, B. J. 1974 The role of potential vorticity in symmetric stability and instability. Q. J. R. Meteorol. Soc. 100 (425), 480–482.Google Scholar
Howard, L. N. 1961 Note on a paper of John W. Miles. J. Fluid Mech. 10, 509–512.Google Scholar
Jacobitz, F. G. & Sarkar, S. 1999 On the shear number effect in stratified shear flow. Theor. Comp. Fluid Dyn. 13 (3), 171–188.Google Scholar
Jacobitz, F. G., Sarkar, S. & van Atta, C. W. 1997 Direct numerical simulations of the turbulence evolution in a uniformly sheared and stably stratified flow. J. Fluid Mech. 342 (1), 231–261.Google Scholar
Lesieur, M. 2008 Turbulence in Fluids, vol. 84, Springer.Google Scholar
Mamatsashvili, G. R., Avsarkisov, V. S., Chagelishvili, G. D., Chanishvili, R. G. & Kalashnik, M. V. 2010 Transient dynamics of nonsymmetric perturbations versus symmetric instability in baroclinic zonal shear flows. J. Atmos. Sci. 97, 2972–2989.Google Scholar
Miles, J. W. 1961 On the stability of heterogeneous shear flows. J. Fluid Mech. 10 (4), 496–508.Google Scholar
Molemaker, M. J., McWilliams, J. C. & Yavneh, I. 2005 Baroclinic instability and loss of balance. J. Phys. Oceanogr. 35, 1505–1517.Google Scholar
Monin, A. S. & Yaglom, A. M. 1971 Statistical Fluid Dynamics, vol. I. Dover.Google Scholar
Müller, P. 1995 Ertel’s potential vorticity theorem in physical oceanography. Rev. Geophys. 33, 67–97.Google Scholar
Noether, E. 1918 Invariant variation problems. Nachr. Ges. Wiss. Göttingen Math-Phys. Klasse 1, 235–237.Google Scholar
Orszag, S. A. & Israeli, M. 1974 Numerical simulation of viscous incompressible flows. Annu. Rev. Fluid Mech. 6 (1), 281–318.Google Scholar
Pedlosky, J. 1987 Geophysical Fluid Dynamics. Springer.Google Scholar
Pieri, A. B., Cambon, C., Godeferd, F. S. & Salhi, A. 2012 Linearized potential vorticity mode and its role in transition to baroclinic instability. Phys. Fluids 24, 076603.Google Scholar
Pierrehumbert, R. T. & Swanson, K. L. 1995 Baroclinic instability. Annu. Rev. Fluid Mech. 27, 419–467.Google Scholar
Plougonven, R. & Zeitlin, V. 2009 Nonlinear development of inertial instability in barotropic shear. Phys. Fluids 21, 106601, 15 pages.Google Scholar
Ripa, P. 1981 Symmetries and conservation laws for internal gravity waves. In AIP Conference Proceedings, vol. 76, p. 281.Google Scholar
Rogallo, R. S. 1981, Numerical Experiments in homogeneous turbulence. NASA Technical Memorandum.Google Scholar
Rohr, J. J., Itsweire, E. C., Helland, K. N. & Atta, C. W. V. 1988 Growth and decay of turbulence in a stably stratified shear flow. J. Fluid Mech. 195 (1), 77–111.Google Scholar
Rossby, C. G. 1940 Planetary flow patterns in the atmosphere. Q. J. R. Meteorol. Soc. 66, 68–87.Google Scholar
Salhi, A. & Cambon, C. 2006 Advances in rapid distortion theory: from rotating shear flows to the baroclinic instability. J. Appl. Mech. 73 (3), 449–460.Google Scholar
Salmon, R. 1982 Hamilton’s principle and Ertel’s theorem. Am. Inst. Phys. Conf. Proc. 88, 127–135.Google Scholar
Salmon, R. 1988 Hamiltonian fluid mechanics. Annu. Rev. Fluid Mech. 20 (1), 225–256.Google Scholar
Shih, L. H., Koseff, J. R., Ferziger, J. H. & Rehmann, C. R. 2000 Scaling and parameterization of stratified homogeneous turbulent shear flow. J. Fluid Mech. 412 (1), 1–20.Google Scholar
Shimizu, M. 1971 The upper atmosphere of Jupiter. Icarus 14 (2), 273–281.Google Scholar
Simon, G., Godeferd, F. S., Cambon, C. & Salhi, A. 2009 From baroclinic instability to developed turbulence. In 19ème Congrès Français de Mécanique.Google Scholar
Stone, P. H. 1966 On non-geostrophic baroclinic stability. J. Atmos. Sci. 23 (4), 390–400.Google Scholar
Stone, P. H. 1970 On non-geostrophic baroclinic stability. Part 2. J. Atmos. Sci. 27, 721–726.Google Scholar
Thorpe, A. S. & Rotunno, R. 1989 Nonlinear aspects of symmetric instability. J. Atmos. Sci. 46 (9), 1285–1299.Google Scholar
Timoumi, M. & Salhi, A. 2009 Equilibrium states in homogeneous turbulence with baroclinic instability. Theoret. Comput. Fluid Dyn. 23, 353–374.Google Scholar
Turner, J. S. 1980 Buoyancy Effects in Fluids. Cambridge University Press.Google Scholar
Vallis, G. K. 2006 Atmospheric and Oceanic Fluid Dynamics: Fundamentals and Large-Scale Circulation. Cambridge University Press.Google Scholar
Young, L. A., Yelle, R. V., Young, R., Seiff, A. & Kirk, D. B. 2005 Gravity waves in Jupiter’s stratosphere, as measured by the Galileo ASI experiment. Icarus 173 (1), 185–199.Google Scholar