Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-26T06:46:52.116Z Has data issue: false hasContentIssue false
  • English
  • Français

Non-normal dynamics of time-evolving co-rotating vortex pairs

Published online by Cambridge University Press:  16 May 2012

X. Mao ,
S. J. Sherwin  and
H. M. Blackburn
X. Mao*
Affiliation:
Department of Aeronautics, Imperial College London, South Kensington SW7 2AZ, UK Department of Mechanical and Aerospace Engineering, Monash University, 3800, Australia
S. J. Sherwin
Affiliation:
Department of Aeronautics, Imperial College London, South Kensington SW7 2AZ, UK
H. M. Blackburn
Affiliation:
Department of Mechanical and Aerospace Engineering, Monash University, 3800, Australia
*
†Email address for correspondence: maoxuerui@sina.com
Get access Rights & Permissions [Opens in a new window]

Abstract

Transient energy growth of disturbances to co-rotating pairs of vortices with axial core flows is investigated in an analysis where vortex core expansion and vortex merging are included by adopting a time-evolving base flow. The dynamics of pairs are compared with those of individual vortices in order to highlight the effect of vortex interaction. Three typical vortex pair cases are studied, with the pairs comprised respectively of individually inviscidly unstable vortices at the streamwise wavenumber that maximizes the individual instabilities, viscously unstable vortices also at the streamwise wavenumber maximizing the individual instabilities and asymptotically stable vortices at streamwise wavenumber zero. For the inviscidly unstable case, the optimal perturbation takes the form of a superposition of two individual helical unstable modes and the optimal energy growth is similar to that predicted for an individual inviscid unstable vortex, while where the individual vortices are viscously unstable, the optimal disturbances within each core have similar spatial distributions to the individually stable case. For both of these cases, time horizons considered are much lower than those required for the merger of the undisturbed vortices. However, for the asymptotically stable case, large linear transient energy growth of optimal perturbations occurs for time horizons corresponding to vortex merging. Linear transient disturbance energy growth exhibited by pairs in this stable case is two to three orders of magnitude larger than that for a corresponding individual vortex. The superposition of the perturbation and the base flow shows that the perturbation has a displacement effect on the vortices in the base flow. Direct numerical simulations of stable pairs seeded by optimal initial perturbations have been carried out and acceleration/delay of vortex merging associated with a dual vortex meandering and vortex breakup related to axially periodic acceleration and delay of vortex merging are observed. For axially invariant cases, the sign of perturbation has an effect, as well as magnitude; the sign dependence relates to whether or not the perturbation adds to or subtracts from the swirl of the base flow. For a two-dimensional perturbation that adds to the swirl of the base flow, seeding with the linear optimal disturbance at a relative energy level 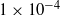induces the pair to move towards each other and approximately halves the time required for merger. Direct numerical simulation shows that the optimal three-dimensional perturbation can induce the vortex system to break up before merging occurs, since the two-dimensional nature of vortex merging is broken by the development of axially periodic perturbations.

JFM classification

Instability: Absolute/convective instability Vortex Flows: Vortex instability Vortex Flows: Vortex interactions
Type
Papers
Information
Journal of Fluid Mechanics , Volume 701 , 25 June 2012 , pp. 430 - 459
Copyright
Copyright © Cambridge University Press 2012

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1. Antkowiak, A. & Brancher, P. 2004 Transient energy growth for the Lamb–Oseen vortex. Phys. Fluids 16 (1) L1–4.Google Scholar
2. Antkowiak, A. & Brancher, P. 2007 On vortex rings around vortices: an optimal mechanism. J. Fluid Mech. 578, 295–304.Google Scholar
3. Barkley, D., Blackburn, H. M. & Sherwin, S. J. 2008 Direct optimal growth analysis for time steppers. Intl J. Numer. Meth. Fluids 57, 1437–1458.Google Scholar
4. Batchelor, G. K. 1964 Axial flow in trailing line vortices. J. Fluid Mech. 20, 645–658.Google Scholar
5. Blackburn, H. M., Barkley, D. & Sherwin, S. J. 2008 Convective instability and transient growth in flow over a backward-facing step. J. Fluid Mech. 603, 271–304.Google Scholar
6. Brion, V., Sipp, D. & Jacquin, L. 2007 Optimal amplification of the Crow instability. Phys. Fluids 19, 111703–1–XX.Google Scholar
7. Broadhurst, M. S. 2007 Vortex stability and breakdown: direct numerical simulation and stability analysis using biglobal and parabolised formulations. PhD thesis, Department of Aeronautics, Imperial College London.Google Scholar
8. Crouch, J. 2005 Airplane trailing vortices and their control. C. R. Physique 6, 487–499.Google Scholar
9. Crow, S. C. 1970 Stability theory for a pair of trailing vortices. AIAA J. 8, 2172–2179.Google Scholar
10. Donnadieu, C., Ortiz, S., Chomaz, J.-M. & Billant, P. 2009 Three-dimensional instabilities and transient growth of a counter-rotating vortex pair. Phys. Fluids 21.Google Scholar
11. Fabre, D. & Jacquin, L. 2004 Viscous instabilities in trailing vortices at large swirl numbers. J. Fluid Mech. 500, 239–262.Google Scholar
12. Fabre, D., Sipp, D. & Jacquin, L. 2006 Kelvin waves and the singular modes of the Lamb–Oseen vortex. J. Fluid Mech. 551, 235–274.Google Scholar
13. Guermond, J. L., Minev, P. & Shen, J. 2006 An overview of projection methods for incompressible flows. Comput. Meth. Appl. Mech. Engng 195, 6011–6045.Google Scholar
14. Heaton, C. J. 2007a Centre modes in inviscid swirling flows and their application to the stability of the Batchelor vortex. J. Fluid Mech. 576, 325–348.Google Scholar
15. Heaton, C. J. 2007b Optimal growth of the Batchelor vortex viscous modes. J. Fluid Mech. 592, 495–505.Google Scholar
16. Heaton, C. J. & Peake, N. 2007 Transient growth in vortices with axial flow. J. Fluid Mech. 587, 271–301.Google Scholar
17. Hussain, F., Pradeep, D. S. & Stout, E. 2011 Nonlinear transient growth in a vortex column. J. Fluid Mech. 682, 304–331.Google Scholar
18. Jiménez, J. 1975 Stability of a pair of co-rotating vortices. Phys. Fluids 18 (11), 1580–1581.Google Scholar
19. Karniadakis, G. E., Israeli, M. & Orszag, S. A. 1991 High-order splitting methods for the incompressible Navier–Stokes equations. J. Comput. Phys. 97 (2), 414–443.Google Scholar
20. Kerswell, R. R. 2002 Elliptic instability. Annu. Rev. Fluid Mech. 34, 83–113.Google Scholar
21. Khorrami, M. R. 1991 On the viscous modes of instability of a trailing line vortex. J. Fluid Mech. 225, 197–212.Google Scholar
22. Lacaze, L., Ryan, K. & Le Dizès, S. 2007 Elliptic instability in a strained Batchelor vortex. J. Fluid Mech. 577, 341–361.Google Scholar
23. Le Dizès, S. & Fabre, D. 2007 Large-Reynolds-number asymptotic analysis of viscous centre modes in vortices. J. Fluid Mech. 585, 153–180.Google Scholar
24. Le Dizès, S. & Laporte, F. 2002 Theoretical predictions for the elliptical instability in a two-vortex flow. J. Fluid Mech. 471, 169–201.Google Scholar
25. Le Dizès, S. & Verga, A. 2002 Viscous interactions of two co-rotating vortices before merging. J. Fluid Mech. 467, 389–410.Google Scholar
26. Lessen, M. & Paillet, F. 1974 The stability of a trailing line vortex. Part 2. Viscous theory. J. Fluid Mech. 65, 769–779.Google Scholar
27. Lessen, M., Singh, P. J. & Paillet, F. 1974 The stability of a trailing line vortex. Part 1. Inviscid theory. J. Fluid Mech. 63, 753–763.Google Scholar
28. Mao, X. 2010 Vortex instability and transient growth. PhD thesis, Imperial College London.Google Scholar
29. Mao, X. & Sherwin, S. J. 2012 Transient growth associated with continuous spectra of the Batchelor vortex. J. Fluid Mech. 697, 35–59.Google Scholar
30. Mao, X., Sherwin, S. J. & Blackburn, H. M. 2011 Transient growth and bypass transition in stenotic flow with a physiological waveform. Theor. Comput. Fluid Dyn. 25 (1), 31–42.Google Scholar
31. Mayer, E. W. & Powell, K. G. 1992 Viscous and inviscid instabilities of a trailing vortex. J. Fluid Mech. 245, 91–114.Google Scholar
32. Meunier, P., Le Dizès, S. & Leweke, T. 2005 Physics of vortex merging. C. R. Physique 6, 431–450.Google Scholar
33. Meunier, P. & Leweke, T. 2005 Elliptic instability of a co-rotating vortex pair. J. Fluid Mech. 533, 125–159.Google Scholar
34. Moore, D. W. & Saffman, P. G. 1975 The instability of a straight vortex filament in a strain field. Proc. R. Soc. Lond. A 346, 413–425.Google Scholar
35. Pradeep, D. S. & Hussain, F. 2006 Transient growth of perturbations in a vortex column. J. Fluid Mech. 550, 251–288.Google Scholar
36. Roy, C., Schaeffer, N., Le Dizès, S. & Thompson, M. C. 2008 Stability of a pair of co-rotating vortices with axial flow. Phys. Fluids 20 (9)094101.Google Scholar
37. Sipp, D., Jacquin, L. & Cossu, C. 2000 Self-adaptation and viscous selection in concentrated two-dimensional dipoles. Phys. Fluids 12, 245–248.Google Scholar
38. Stewartson, K. & Brown, S. N. 1985 Near-neutral centre-modes as inviscid perturbations to a trailing line vortex. J. Fluid Mech. 156, 387–399.Google Scholar
39. Tsai, C. & Widnall, S. 1976 The stability of short waves on a straight vortex filament in a weak externally imposed strain field. J. Fluid Mech. 73, 721–733.Google Scholar
40. Tuckerman, L. S. & Barkley, D. 2000 Bifurcation analysis for time steppers. In Numerical Methods for Bifurcation Problems and Large-Scale Dynamical Systems (ed. Doedel, E. & Tuckerman, L. S. ). pp. 453–566. Springer.Google Scholar