Hostname: page-component-586b7cd67f-gb8f7 Total loading time: 0 Render date: 2024-11-28T09:44:52.523Z Has data issue: false hasContentIssue false
  • English
  • Français

Numerical calculations of two-dimensional large Prandtl number convection in a box

Published online by Cambridge University Press:  24 July 2013

J. A. Whitehead ,
A. Cotel ,
S. Hart ,
C. Lithgow-Bertelloni  and
W. Newsome
J. A. Whitehead*
Affiliation:
Physical Oceanography Department, Woods Hole Oceanographic Institution, Woods Hole, MA 02543, USA
A. Cotel
Affiliation:
Civil and Environmental Engineering Department, University of Michigan, 1351 Beal Avenue, Ann Arbor, MI 48109, USA
S. Hart
Affiliation:
Geology and Geophysics Department, Woods Hole Oceanographic Institution, Woods Hole, MA 02543, USA
C. Lithgow-Bertelloni
Affiliation:
Department of Earth Sciences, University College London, Gower Street, London WC1E 6BT, UK
W. Newsome
Affiliation:
Geological Sciences Department, University of Michigan, 1100 North University Avenue, Ann Arbor, MI 48109, USA
*
†Email address for correspondence: jwhitehead@whoi.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

Convection from an isolated heat source in a chamber has been previously studied numerically, experimentally and analytically. These have not covered long time spans for wide ranges of Rayleigh number Ra and Prandtl number Pr. Numerical calculations of constant viscosity convection partially fill the gap in the ranges 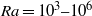$\mathit{Ra}= 1{0}^{3} {{\unicode{x2013}}}1{0}^{6} $ and 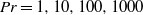$\mathit{Pr}= 1, 10, 100, 1000$ and 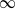$\infty $. Calculations begin with cold fluid everywhere and localized hot temperature at the centre of the bottom of a square two-dimensional chamber. For 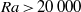$\mathit{Ra}\gt 20\hspace{0.167em} 000$, temperature increases above the hot bottom and forms a rising plume head. The head has small internal recirculation and minor outward conduction of heat during ascent. The head approaches the top, flattens, splits and the two remnants are swept to the sidewalls and diffused away. The maximum velocity and the top centre heat flux climb to maxima during head ascent and then adjust toward constant values. Two steady cells are separated by a vertical thermal conduit. This sequence is followed for every value of 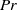$Pr$ number, although lower Pr convection lags in time. For 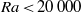$\mathit{Ra}\lt 20\hspace{0.167em} 000$ there is no plume head, and no streamfunction and heat flux maxima with time. For sufficiently large Ra and all values of Pr, an oscillation develops at roughly 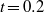$t= 0. 2$, with the two cells alternately strengthening and weakening. This changes to a steady flow with two unequal cells that at roughly 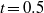$t= 0. 5$ develops a second oscillation.

JFM classification

Convection: Buoyant boundary layers Convection: Convection in cavities Convection: Plumes/thermals
Type
Papers
Information
Journal of Fluid Mechanics , Volume 729 , 25 August 2013 , pp. 584 - 602
Copyright
©2013 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Busse, F. H. 1972 The oscillatory instability of convection rolls in a low Prandtl number fluid. J. Fluid Mech. 52, 97–112.Google Scholar
Busse, F. H. & Whitehead, J. A. 1974 Oscillatory and collective instabilities in large Prandtl number convection. J. Fluid Mech. 66, 67–80.Google Scholar
Chay, A. & Shlien, D. J. 1986 Scalar field measurements of a laminar starting plume cap using digital processing of interferograms. Phys. Fluids 2, 2358–2366.Google Scholar
Couliette, D. L. & Loper, D. E. 1995 Experimental, numerical, and analytical models of mantle starting plumes. Phys. Earth Planet. Inter. 92, 143–167.Google Scholar
Davaille, A. & Jaupart, C. 1993 Transient high-Rayleigh number thermal convection with large viscosity variations. J. Fluid Mech. 253, 141–166.Google Scholar
Davaille, A., Limare, A., Touitou, F., Kumagai, I. & Vatteville, J. 2011 Anatomy of a starting plume at high Prandtl number. Exp. Fluids 50, 285–300.Google Scholar
Durran, D. R. 1999 Numerical Methods for Wave Equations in Geophysical Fluid Dynamics. Springer.Google Scholar
Farnetani, C. G. & Hofmann, A. W 2009 Dynamics and internal structure of a lower mantle plume conduit. Earth Planet. Sci. Lett. 282, 314–322.Google Scholar
Griffiths, R. W. 1986 Thermals in extremely viscous fluids, including the effects of temperature-dependent viscosity. J. Fluid Mech. 66, 115–138.Google Scholar
Griffiths, R. W. & Campbell, I. H. 1990 Stirring and structure in mantle starting plumes. Earth Planet. Sci. Lett. 99, 66–78.CrossRefGoogle Scholar
van Keken, P. E., Davaille, A. & Vatteville, J. 2009 Dynamics of a laminar plume in a cavity: the influence of boundaries on the steady-state stem structure. Geochem. Geophys. Geosyst. 14, 1–21.Google Scholar
Krishnamurti, R 1970 On the transition to turbulent convection. Part 2. The transition to time-dependent flow. J. Fluid Mech. 42, 309–320.Google Scholar
Hier-Majumder, C. A., Yuen, D. A., Sevre, E. O., Boggs, J. M. & Bergeron, S. Y. 2002 Finite Prandtl number 2-D convection at high Rayleigh numbers. Electron. Geosci. 7, 11–30; Visual Geosci. 2, 1–53.Google Scholar
Olson, P. & Singer, H. 1985 Creeping plumes. J. Fluid Mech. 158, 509–529.Google Scholar
Richards, M. A., Duncan, R. A. & Courtillot, V. E. 1989 Flood basalts and hot-spot tracks: plume heads and tails. Science 246, 103–107.Google Scholar
Schubert, G., Turcotte, D. L. & Olson, P. 2001 Mantle Convection in the Earth and Planets. Cambridge University Press.Google Scholar
Suetsugu, D., Steinberger, B. & Kogiso, T. 2005 Mantle plumes and hot spots. In Encyclopedia of Geology, pp. 335–343. Elsevier.Google Scholar
Turner, J. S. 1962 The starting plume in neutral surroundings. J. Fluid Mech. 13, 356–368.Google Scholar
Vatteville, J., van Keken, P., Limare, A. & Davaille, A. 2009 Starting laminar plumes: comparison of laboratory and numerical modelling. Geochem. Geophys. Geosyst. 10, Q12013.Google Scholar
Whitehead, J. A. & Luther, D. S. 1975 Dynamics of laboratory diapir and plume models. J. Geophys. Res. 80, 705–717.Google Scholar