Hostname: page-component-78c5997874-xbtfd Total loading time: 0 Render date: 2024-11-19T09:16:38.717Z Has data issue: false hasContentIssue false
  • English
  • Français

A numerical investigation of the asymmetric wake mode of a squareback Ahmed body – effect of a base cavity

Published online by Cambridge University Press:  17 October 2017

J.-M. Lucas ,
O. Cadot Open the ORCID record for O. Cadot [Opens in a new window] ,
V. Herbert ,
S. Parpais  and
J. Délery
J.-M. Lucas
Affiliation:
GANTHA, 12 Boulevard Chasseigne, 86000 Poitiers, France
O. Cadot*
Affiliation:
IMSIA, ENSTA-ParisTech/CNRS/CEA/EDF, Université Paris Saclay, 828 Boulevard des Maréchaux, 91762 Palaiseau CEDEX, France
V. Herbert
Affiliation:
PSA Peugeot Citroën, Route de Gisy, 78140 Vélizy-Villacoublay, France
S. Parpais
Affiliation:
Renault SAS, 13/15 Quai Alphonse le Gallo, 92100 Boulogne-Billancourt, France
J. Délery
Affiliation:
GIE S2A, 2 Avenue Volta, 78180 Montigny-le-Bretonneux, France
*
†Email address for correspondence: cadot@ensta.fr
Get access Rights & Permissions [Opens in a new window]

Abstract

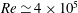Numerical simulations of the turbulent flow over the flat backed Ahmed model at Reynolds number $Re\simeq 4\times 10^{5}$ are conducted using a lattice Boltzmann solver to clarify the mean topology of the static symmetry-breaking mode of the wake. It is shown that the recirculation region is occupied by a skewed low pressure torus, whose part closest to the body is responsible for an extra low pressure imprint on the base. Shedding of one-sided vortex loops is also reported, indicating global quasi-periodic dynamics in conformity with the seminal work of Grandemange et al. (J. Fluid Mech., vol. 722, 2013, pp. 51–84). Despite the limited low frequency resolution of the simulation, power spectra of the lateral velocity fluctuations at different locations corroborate the presence of this quasi-periodic mode at a Strouhal number of 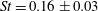$St=0.16\pm 0.03$. A shallow base cavity of 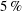$5\,\%$ of the body height reduces the drag coefficient by 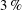$3\,\%$ but keeps the recirculating torus and its interaction with the base mostly unchanged. The drag reduction lies in a global constant positive shift of the base pressure distribution. For a deep base cavity of 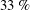$33\,\%$ of the body height, a drag reduction of 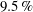$9.5\,\%$ is obtained. It is accompanied by a large elongation of the recirculation inside the cavity that considerably attenuates the low pressure sources therein together with a symmetrization of the low pressure torus. The global quasi-periodic mode is found to be inhibited by the cavity.

JFM classification

Flow Control: Instability control Wakes/Jets: Separated flows Wakes/Jets: Wakes
Type
Papers
Information
Journal of Fluid Mechanics , Volume 831 , 25 November 2017 , pp. 675 - 697
Check for updates
Copyright
© 2017 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abernathy, F. H. & Kronauer, R. E. 1962 The formation of vortex streets. J. Fluid Mech. 13 (1), 1–20.Google Scholar
Afzal, N. 1996 Wake layer in a turbulent boundary layer with pressure gradient: a new approach. In IUTAM Symposium on Asymptotic Methods for Turbulent Shear Flows at High Reynolds Numbers (ed. Gersten, K.), pp. 95–118. Springer.Google Scholar
Barros, D., Ruiz, T., Borée, J. & Noack, B. R. 2014 Control of three-dimensionnal blunt body wake using low and high frequency pulsed jets. Intl J. Flow Control 6 (1), 61–74.Google Scholar
Bayraktar, I., Landman, D. & Baysal, O.2001 Experimental and computational investigation of Ahmed body for ground vehicle aerodynamics. SAE Tech. Paper Series 2001-01-2742.Google Scholar
Bhatnagar, P. L., Gross, E. P. & Krook, M. 1954 A model for collision processes in gases. 1. Small amplitude processes in charged and neutral one-component systems. Phys. Rev. 94, 511–525.CrossRefGoogle Scholar
Bohorquez, P., Sanmiguel-Rojas, E., Sevilla, A., Jiménez-González, J. I. & Martínez-Bazán, C. 2011 Stability and dynamics of the laminar wake past a slender blunt-based axisymmetric body. J. Fluid Mech. 676, 110–144.Google Scholar
Brackston, R. D., Garci De La Cruz, J. M., Wynn, A., Rigas, G. & Morrison, J. F. 2016 Stochastic modelling and feedback control of bistability in a turbulent bluff body wake. J. Fluid Mech. 802, 726–749.Google Scholar
Bury, Y. & Jardin, T. 2014 Wake instabilities behind an axisymmetric bluff body at low Reynolds numbers. Notes Numer. Fluid Mech. Multidisciplinary Design 125, 31–37.Google Scholar
Cadot, O. 2016 Stochastic fluid structure interaction of three-dimensional plates facing a uniform flow. J. Fluid Mech. 794, R1.CrossRefGoogle Scholar
Cadot, O., Evrard, A. & Pastur, L. 2015 Imperfect supercritical bifurcation in a three-dimensional turbulent wake. Phys. Rev. E 91 (6).Google Scholar
Cercignani, C. 1988 The Boltzmann Equation, pp. 40–103. Springer.CrossRefGoogle Scholar
Chen, S. & Doolen, G. D. 1998 Lattice Boltzmann method for fluid flows. Annu. Rev. Fluid Mech. 30 (1), 329–364.CrossRefGoogle Scholar
Duell, E. G. & George, A. R. 1999 Experimental study of a ground vehicle body unsteady near wake. SAE Trans. 108, 1589–1602; (6, part 1).Google Scholar
Evrard, A., Cadot, O., Herbert, V., Ricot, D., Vigneron, R. & Délery, J. 2016 Fluid force and symmetry breaking modes of a 3D bluff body with a base cavity. J. Fluids Struct. 61, 99–114.CrossRefGoogle Scholar
Evstafyeva, O., Morgans, A. & Dalla Longa, L. 2017 Simulation and feedback control of the Ahmed body flow exhibiting symmetry breaking behaviour. J. Fluid Mech. 817, R2.Google Scholar
Fabre, D., Auguste, F. & Magnaudet, J. 2008 Bifurcations and symmetry breaking in the wake of axisymmetric bodies. Phys. Fluids 20, 051702.CrossRefGoogle Scholar
Filippova, O. & Hänel, D. 1998 Grid refinement for lattice-BGK models. J. Comput. Phys. 147 (1), 219–228.CrossRefGoogle Scholar
Gentile, V., Schrijer, F. F. J., Van Oudheusden, B. W. & Scarano, F. 2016 Low-frequency behavior of the turbulent axisymmetric near-wake. Phys. Fluids 28 (6), 065102.CrossRefGoogle Scholar
Gentile, V., Van Oudheusden, B. W., Schrijer, F. F. J. & Scarano, F. 2017 The effect of angular misalignment on low-frequency axisymmetric wake instability. J. Fluid Mech. 813, R3.CrossRefGoogle Scholar
Gerrard, J. H. 1966 The mechanics of the formation region of vortices behind bluff bodies. J. Fluid Mech. 25 (02), 401–413.Google Scholar
Grandemange, M.2013 Analysis and control of three-dimensional turbulent wakes: from axisymmetric bodies to real road vehicles. PhD thesis, ENSTA Paris Tech.Google Scholar
Grandemange, M., Gohlke, M. & Cadot, O. 2012a Reflectional symmetry breaking of the separated flow over three-dimensional bluff bodies. Phys. Rev. E 86, 035302.Google ScholarPubMed
Grandemange, M., Gohlke, M. & Cadot, O. 2013a Bi-stability in the turbulent wake past parallelepiped bodies with various aspect ratios and wall effects. Phys. Fluids 25, 095103.CrossRefGoogle Scholar
Grandemange, M., Gohlke, M. & Cadot, O. 2013b Turbulent wake past a three-dimensional blunt body. Part 1. Global modes and bi-stability. J. Fluid Mech. 722, 51–84.Google Scholar
Grandemange, M., Gohlke, M. & Cadot, O. 2014a Statistical axisymmetry of the turbulent sphere wake. Exp. Fluids 55 (11), 1–10.Google Scholar
Grandemange, M., Gohlke, M. & Cadot, O. 2014b Turbulent wake past a three-dimensional blunt body. Part 2. Experimental sensitivity analysis. J. Fluid Mech. 752, 439–461.Google Scholar
Grandemange, M., Parezanović, V., Gohlke, M. & Cadot, O. 2012b On experimental sensitivity analysis of the turbulent wake from an axisymmetric blunt trailing edge. Phys. Fluids 24, 035106.Google Scholar
He, X. & Luo, L. S. 1997 A priori derivation of the lattice Boltzmann equation. Phys. Rev. E 55 (6), R6333–R6336.Google Scholar
Krajnović, S. & Davidson, L. 2003 Numerical study of the flow around a bus-shaped body. Trans. ASME J. Fluids Engng 125, 500.CrossRefGoogle Scholar
Kruiswyk, R. W. & Dutton, J. C. 1990 Effect of a base cavity on subsonic near-wake flow. AIAA J. 28 (11), 1885–1893.CrossRefGoogle Scholar
LaBS2014 Lattice-Boltzmann Solver LaBS, http://www.labs-project.org.Google Scholar
Lévêque, E, Toschi, F., Shao, L. & Bertoglio, J.-P. 2007 Shear-improved Smagorinsky model for large-eddy simulation of wall-bounded turbulent flows. J. Fluid Mech. 570, 491–502.Google Scholar
Li, R., Barros, D., Borée, J., Cadot, O., Noack, B. R. & Cordier, L. 2016 Feedback control of bimodal wake dynamics. Exp. Fluids 57 (10), 158.CrossRefGoogle Scholar
Liou, W. W. 1994 Linear instability of curved free shear layers. Phys. Fluids 6 (2), 541–549.CrossRefGoogle Scholar
Malaspinas, O. & Sagaut, P. 2011 Advanced large-eddy simulation for lattice Boltzmann methods: The approximate deconvolution model. Phys. Fluids 23 (10), 105103.Google Scholar
Marquet, O. & Larsson, M. 2014 Global wake instabilities of low aspect-ratio flat-plates. Eur. J. Mech. (B/Fluids) 49 (–1), 400–412.CrossRefGoogle Scholar
Martin-Alcantara, A., Sanmiguel-Rojas, E., Gutierrez-Montes, C. & Martinez-Bazan, C. 2014 Drag reduction induced by the addition of a multi-cavity at the base of a bluff body. J. Fluids Struct. 48, 347–361.CrossRefGoogle Scholar
Meliga, P., Chomaz, J. M. & Sipp, D. 2009 Unsteadiness in the wake of disks and spheres: instability, receptivity and control using direct and adjoint global stability analyses. J. Fluids Struct. 25 (4), 601–616.Google Scholar
Mittal, R., Wilson, J. J. & Najjar, F. M. 2002 Symmetry properties of the transitional sphere wake. AIAA J. 40 (3), 579–582.CrossRefGoogle Scholar
Molezzi, MJ & Dutton, JC 1995 Study of subsonic base cavity flowfield structure using particle image velocimetry. AIAA J. 33 (2), 201–209.Google Scholar
Östh, J., Noack, B. R., Krajnović, S., Barros, D. & Borée, J. 2014 On the need for a nonlinear subscale turbulence term in POD models as exemplified for a high-Reynolds-number flow over an Ahmed body. J. Fluid Mech. 747, 518–544.Google Scholar
Pasquetti, R. & Peres, N. 2015 A penalty model of synthetic micro-jet actuator with application to the control of wake flows. Comput. Fluids 114 (0), 203–217.Google Scholar
Patel, V. C. & Sotiropoulos, F. 1997 Longitudinal curvature effects in turbulent boundary layers. Prog. Aerosp. Sci. 33 (1), 1–70.Google Scholar
Perry, A.-K., Pavia, G. & Passmore, M. 2016 Influence of short rear end tapers on the wake of a simplified square-back vehicle: wake topology and rear drag. Exp. Fluids 57 (11), 169.CrossRefGoogle Scholar
Pier, B. 2008 Local and global instabilities in the wake of a sphere. J. Fluid Mech. 603, 39–61.CrossRefGoogle Scholar
Ricot, D., Marié, S., Sagaut, P. & Bailly, C. 2009 Lattice Boltzmann method with selective viscosity filter. J. Comput. Phys. 228 (12), 4478–4490.Google Scholar
Rigas, G., Morgans, A. S., Brackston, R. D. & Morrison, J. F. 2015a Diffusive dynamics and stochastic models of turbulent axisymmetric wakes. J. Fluid Mech. 778, R2.CrossRefGoogle Scholar
Rigas, G., Morgans, A. S. & Morrison, J. F. 2015b Stability and coherent structures in the wake of axisymmetric bluffbodies. Fluid Mech. Applics. 107, 143–148.Google Scholar
Rigas, G., Oxlade, A. R., Morgans, A. S. & Morrison, J. F. 2014 Low-dimensional dynamics of a turbulent axisymmetric wake. J. Fluid Mech. 755, 159.Google Scholar
Rouméas, M., Gilliéron, P. & Kourta, A. 2009 Analysis and control of the near-wake flow over a squareback geometry. Comput. Fluids 38 (1), 60–70.Google Scholar
Sanmiguel-Rojas, E. & Mullin, T. 2012 Finite-amplitude solutions in the flow through a sudden expansion in a circular pipe. J. Fluid Mech. 691, 201–213.CrossRefGoogle Scholar
Stolz, S., Adams, N. A. & Kleiser, L. 2001 An approximate deconvolution model for large-eddy simulation with application to incompressible wall-bounded flows. Phys. Fluids 13 (4), 997–1015.CrossRefGoogle Scholar
Thompson, M. C., Leweke, T. & Provansal, M. 2001 Kinematics and dynamics of sphere wake transition. J. Fluids Struct. 15 (3–4), 575–585.CrossRefGoogle Scholar
Touil, H., Ricot, D. & Lévêque, E. 2014 Direct and large-eddy simulation of turbulent flows on composite multi-resolution grids by the lattice Boltzmann method. J. Comput. Phys. 256, 220–233.Google Scholar
Verschaeve, J. C. G. & Müller, B. 2010 A curved no-slip boundary condition for the lattice Boltzmann method. J. Comput. Phys. 229 (19), 6781–6803.CrossRefGoogle Scholar
Volpe, R., Devinant, P. & Kourta, A. 2015 Experimental characterization of the unsteady natural wake of the full-scale square back ahmed body: flow bi-stability and spectral analysis. Exp. Fluids 56 (5), 1–22.Google Scholar
Wassen, E., Eichinger, S. & Thiele, F. 2010 Simulation of active drag reduction for a square-back vehicle. Notes Numer. Fluid Mech. Multidisciplinary Design 108, 241–255.Google Scholar
Yun, G., Kim, D. & Choi, H. 2006 Vortical structures behind a sphere at subcritical Reynolds numbers. Phys. Fluids 18, 015102.CrossRefGoogle Scholar