Hostname: page-component-586b7cd67f-tf8b9 Total loading time: 0 Render date: 2024-11-28T00:55:33.794Z Has data issue: false hasContentIssue false
  • English
  • Français

Numerical investigation of the effect of airfoil thickness on onset of dynamic stall

Published online by Cambridge University Press:  15 May 2019

Anupam Sharma Open the ORCID record for Anupam Sharma [Opens in a new window]  and
Miguel Visbal
Anupam Sharma*
Affiliation:
Department of Aerospace Engineering, Iowa State University, Ames, IA 50011, USA
Miguel Visbal
Affiliation:
Air Force Research Laboratory, Wright-Patterson AFB, OH 45433, USA
*
†Email address for correspondence: sharma@iastate.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

Effect of airfoil thickness on onset of dynamic stall is investigated using large eddy simulations at chord-based Reynolds number of 200 000. Four symmetric NACA airfoils of thickness-to-chord ratios of 9 %, 12 %, 15 % and 18 % are studied. The three-dimensional Navier–Stokes solver, FDL3DI is used with a sixth-order compact finite difference scheme for spatial discretization, second-order implicit time integration and discriminating filters to remove unresolved wavenumbers. A constant-rate pitch-up manoeuver is studied with the pitching axis located at the airfoil quarter chord. Simulations are performed in two steps. In the first step, the airfoil is kept static at a prescribed angle of attack (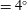$=4^{\circ }$). In the second step, a ramp function is used to smoothly increase the pitch rate from zero to the selected value and then the pitch rate is held constant until the angle of attack goes past the lift-stall point. The solver is verified against experiments for flow over a static NACA 0012 airfoil. Static simulation results of all airfoil geometries are also compared against XFOIL predictions with a generally favourable agreement. FDL3DI predicts two-stage transition for thin airfoils (9 % and 12 %), which is not observed in the XFOIL results. The dynamic simulations show that the onset of dynamic stall is marked by the bursting of the laminar separation bubble (LSB) in all the cases. However, for the thickest airfoil tested, the reverse flow region spreads over most of the airfoil and reaches the LSB location immediately before the LSB bursts and dynamic stall begins, suggesting that the stall could be triggered by the separated turbulent boundary layer. The results suggest that the boundary between different classifications of dynamic stall, particularly leading edge stall versus trailing edge stall, is blurred. The dynamic-stall onset mechanism changes gradually from one to the other with a gradual change in some parameters, in this case, airfoil thickness.

JFM classification

Boundary Layers: Boundary layer separation
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 870 , 10 July 2019 , pp. 870 - 900
Copyright
© 2019 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Barnes, C. J. & Visbal, M. R. 2016 Aeroelastic response of an airfoil at transitional Reynolds numbers. In 46th AIAA Fluid Dynamics Conference. p. 3634. American Institute of Aeronautics and Astronautics.Google Scholar
Benton, S. I. & Visbal, M. R. 2018 Understanding abrupt leading edge separation as a mechanism for the onset of dynamic stall. In 56th AIAA Aerospace Sciences Meeting. Kissimmee, Florida, USA. American Institute of Aeronautics and Astronautics.Google Scholar
Bodling, A. & Sharma, A. 2017 Noise reduction mechanisms due to bio-inspired airfoil designs. In 17th International Symposium on Transport Phenomena and Dynamics of Rotating Machinery. Maui, HI, USA.Google Scholar
Bodling, A. & Sharma, A. 2019 Numerical investigation of low-noise airfoils inspired by the down coat of owls. Bioinspir. Biomim. 14 (1), 016013.Google Scholar
Brandon, J. M.1991 Dynamic stall effects and applications to high performance aircraft. Tech. Rep. AGARD-R-776. National Institute of Aeronautics and Astronautics.Google Scholar
Carr, L. W. 1988 Progress in analysis and prediction of dynamic stall. J. Aircraft 25 (1), 6–17.Google Scholar
Carr, L. W. & Chandrasekhara, M. S. 1996 Compressibility effects on dynamic stall. Prog. Aerosp. Sci. 32 (6), 523–573.Google Scholar
Carr, L. W., McAlister, K. W. & McCroskey, W. J.1977 Analysis of the development of dynamic stall based on oscillating airfoil experiments. Tech. Rep. NASA TN D-8382. National Aeronautics and Space Administration.Google Scholar
Chandrasekhara, M. S. & Carr, L. W. 1990 Flow visualization studies of the Mach number effects on dynamic stall of an oscillating airfoil. J. Aircraft 27 (6), 516–522.Google Scholar
Corke, T. C. & Thomas, F. O. 2015 Dynamic stall in pitching airfoils: aerodynamic damping and compressibility effects. Annu. Rev. Fluid Mech. 47, 479–505.Google Scholar
Drela, M. 1989 Xfoil: an analysis and design system for low Reynolds number airfoils. In Low Reynolds Number Aerodynamics, pp. 1–12. Springer.Google Scholar
Ekaterinaris, J. A. 1995 Numerical investigation of dynamic stall of an oscillating wing. AIAA J. 33 (10), 1803–1808.Google Scholar
Ekaterinaris, J. A. & Platzer, M. F. 1998 Computational prediction of airfoil dynamic stall. Prog. Aerosp. Sci. 33 (11), 759–846.Google Scholar
Ericsson, L. E. & Reding, J. P. 1988 Fluid mechanics of dynamic stall part I. Unsteady flow concepts. J. Fluids Struct. 2 (1), 1–33.Google Scholar
Fujisawa, N. & Shibuya, S. 2001 Observations of dynamic stall on darrieus wind turbine blades. J. Wind Engng Ind. Aerodyn. 89 (2), 201–214.Google Scholar
Garcia-Sagrado, A. & Hynes, T. 2012 Wall pressure sources near an airfoil trailing edge under turbulent boundary layers. J. Fluids Struct. 30, 3–34.Google Scholar
Garmann, D. J. & Visbal, M. R. 2011 Numerical investigation of transitional flow over a rapidly pitching plate. Phys. Fluids 23, 094106.Google Scholar
Garmann, D. J. & Visbal, M. R. 2015 Interactions of a streamwise-oriented vortex with a finite wing. J. Fluid Mech. 767, 782–810.Google Scholar
Garmann, D. J., Visbal, M. R. & Orkwis, P. D. 2013a Comparative study of implicit and subgrid-scale model large-eddy simulation techniques for low-Reynolds number airfoil applications. Intl J. Numer. Meth. Fluids 71 (12), 1546–1565.Google Scholar
Garmann, D. J., Visbal, M. R. & Orkwis, P. D. 2013b Three-dimensional flow structure and aerodynamic loading on a revolving wing. Phys. Fluids 25 (3), 034101.Google Scholar
Gregory, N. & O’reilly, C. L.1973 Low-speed aerodynamic characteristics of NACA 0012 aerofoil section, including the effects of upper-surface roughness simulating hoar frost. Tech. Rep. R&M No. 3726. Aeronautical Research Council.Google Scholar
Gupta, R. & Ansell, P. J. 2017 Unsteady flow physics of airfoil dynamic stall. In 55th AIAA Aerospace Sciences Meeting, American Institute of Aeronautics and Astronautics, AIAA 2017-0999.Google Scholar
Haller, G. 2002 Lagrangian coherent structures from approximate velocity data. Phys. Fluids 14 (6), 1851–1861.Google Scholar
Ham, N. D. & Garelick, M. S. 1968 Dynamic stall considerations in helicopter rotors. J. Am. Helicopter Soc. 13 (2), 49–55.Google Scholar
Heine, B., Mulleners, K., Joubert, G. & Raffel, M. 2013 Dynamic stall control by passive disturbance generators. AIAA J. 51 (9), 2086–2097.Google Scholar
Huebsch, W. W. & Rothmayer, A. P. 2002 Effects of surface ice roughness on dynamic stall. J. Aircraft 39 (6), 945–953.Google Scholar
Jones, R. T.1940 The unsteady lift of a wing of finite aspect ratio. Tech. Rep. NACA TN 2925. NASA Langley Research Center.Google Scholar
Kármán, T. V. & Sears, W. R. 1938 Airfoil theory of non-uniform motion. J. Aero. Sci. 5 (10), 379–390.Google Scholar
Kramer, V. M. 1932 Die zunahme des maximalauftriebes von tragflugeln bei plotzlicher anstellwinkelvergrosserung (boeneffekt). Z. Flugtech. Motorluftschiff 23, 185–189.Google Scholar
Larsen, J. W., Nielsen, S. R. K. & Krenk, S. 2007 Dynamic stall model for wind turbine airfoils. J. Fluids Struct. 23 (7), 959–982.Google Scholar
Leishman, J. G. & Beddoes, T. S. 1989 A semi-empirical model for dynamic stall. J. Am. Helicopter Soc. 34 (3), 3–17.Google Scholar
Lele, S. K. 1992 Compact finite difference schemes with spectral-like resolution. J. Comput. Phys. 103 (1), 16–42.Google Scholar
Li, Y. & Wang, Z. J. 2016 A priori and a posteriori evaluations of sub-grid scale models for the burgers’ equation. Comput. Fluids 139, 92–104.Google Scholar
Lomax, H.1953 Lift developed on unrestrained rectangular wings entering gusts at subsonic and supersonic speeds. Rep. NACA TN 2925. National Aeronautics and Space Administration.Google Scholar
Lorber, P. F. & Carta, F. O. 1988 Airfoil dynamic stall at constant pitch rate and high Reynolds number. J. Aircraft 25 (6), 548–556.Google Scholar
McCroskey, W. J.1981 The phenomenon of dynamic stall. Tech. Rep. NASA Technical Memorandum 81264. NASA Ames Research Center, Moffett Field, California, USA.Google Scholar
McCroskey, W. J. 1982 Unsteady airfoils. Annu. Rev. Fluid Mech. 14 (1), 285–311.Google Scholar
McCroskey, W. J., McAlister, K. W., Carr, L. W., Pucci, S. L., Lambert, O. & Indergrand, R. F. 1981 Dynamic stall on advanced airfoil sections. J. Am. Helicopter Soc. 26 (3), 40–50.Google Scholar
Mulleners, K. & Raffel, M. 2012 The onset of dynamic stall revisited. Exp. Fluids 52 (3), 779–793.Google Scholar
Mulleners, K. & Raffel, M. 2013 Dynamic stall development. Exp. Fluids 54 (2), 1469.Google Scholar
Müller-Vahl, H. F., Nayeri, C. N., Paschereit, C. O. & Greenblatt, D. 2016 Dynamic stall control via adaptive blowing. J. Renew. Energy 97, 47–64.Google Scholar
Müller-Vahl, H. F., Strangfeld, C., Nayeri, C. N., Paschereit, C. O. & Greenblatt, D. 2014 Control of thick airfoil, deep dynamic stall using steady blowing. AIAA J. 53 (2), 277–295.Google Scholar
Ramesh, K., Gopalarathnam, A., Ol, M. V., Granlund, K. & Edwards, J. R. 2011 Augmentation of inviscid airfoil theory to predict and model 2d unsteady vortex dominated flows. In 41st AIAA Fluid Dynamics Conference and Exhibit. American Institute of Aeronautics and Astronautics.Google Scholar
Rosti, M. E., Omidyeganeh, M. & Pinelli, A. 2016 Direct numerical simulation of the flow around an aerofoil in ramp-up motion. Phys. Fluids 28 (2), 025106.Google Scholar
Sears, W. R. 1941 Some aspects of non-stationary airfoil theory and its practical application. J. Aero. Sci. 8 (3), 104–108.Google Scholar
Theodorsen, T. & Mutchler, W. H.1935 General theory of aerodynamic instability and the mechanism of flutter. Rep. National Aeronautics and Space Administration.Google Scholar
Visbal, M. R. 1990 Dynamic stall of a constant-rate pitching airfoil. J. Aircraft 27 (5), 400–407.Google Scholar
Visbal, M. R. 2009 High-fidelity simulation of transitional flows past a plunging airfoil. AIAA J. 47 (11), 2685–2697.Google Scholar
Visbal, M. R. 2011 Numerical investigation of deep dynamic stall of a plunging airfoil. AIAA J. 49 (10), 2152–2170.Google Scholar
Visbal, M. R. & Benton, S. I. 2018 Exploration of high-frequency control of dynamic stall using large-eddy simulations. AIAA J. 56 (8), 2974–2991.Google Scholar
Visbal, M. R. & Garmann, D. 2018 Analysis of the onset of dynamic stall on a pitching airfoil using high-fidelity large-eddy simulations. AIAA J. 56 (1), 46–63.Google Scholar
Visbal, M. R. & Garmann, D. J. 2017 Numerical investigation of spanwise end effects on dynamic stall of a pitching NACA 0012 wing. In 55th AIAA Aerospace Sciences Meeting, Denver, Colorado, USA. American Institute of Aeronautics and Astronautics.Google Scholar
Visbal, M. R. & Rizzetta, D. P. 2002 Large-eddy simulation on curvilinear grids using compact differencing and filtering schemes. J. Fluids Engng 124 (4), 836–847.Google Scholar
Visbal, R. M. & Gaitonde, V. D. 2002 On the use of higher-order finite-difference schemes on curvilinear and deforming meshes. J. Comput. Phys. 181 (1), 155–185.Google Scholar
Wagner, H. 1925 Über die entstehung des dynamischen auftriebes von tragflügeln. Z. Angew. Math. Mech. J. Appl. Math. Mech. 5 (1), 17–35.Google Scholar