Hostname: page-component-cd9895bd7-gxg78 Total loading time: 0 Render date: 2024-12-17T15:17:58.125Z Has data issue: false hasContentIssue false
  • English
  • Français

Numerical simulations of lock-exchange compositional gravity current

Published online by Cambridge University Press:  10 September 2009

SENG KEAT OOI ,
GEORGE CONSTANTINESCU  and
LARRY WEBER
SENG KEAT OOI
Affiliation:
Civil and Environmental Engineering, IIHR-Hydroscience and Engineering, C. Maxwell Stanley Hydraulics Laboratory, University of Iowa, Iowa City, IA 52242, USA
GEORGE CONSTANTINESCU*
Affiliation:
Civil and Environmental Engineering, IIHR-Hydroscience and Engineering, C. Maxwell Stanley Hydraulics Laboratory, University of Iowa, Iowa City, IA 52242, USA
LARRY WEBER
Affiliation:
Civil and Environmental Engineering, IIHR-Hydroscience and Engineering, C. Maxwell Stanley Hydraulics Laboratory, University of Iowa, Iowa City, IA 52242, USA
*
†Email address for correspondence: sconstan@engineering.uiowa.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

Compositional gravity current flows produced by the instantaneous release of a finite-volume, heavier lock fluid in a rectangular horizontal plane channel are investigated using large eddy simulation. The first part of the paper focuses on the evolution of Boussinesq lock-exchange gravity currents with a large initial volume of the release during the slumping phase in which the front of the gravity current propagates with constant speed. High-resolution simulations are conducted for Grashof numbers 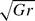= 3150 (LGR simulation) and 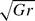= 126000 (HGR simulation). The Grashof number is defined with the channel depth h and the buoyancy velocity ub = 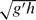(g′ is the reduced gravity). In the HGR simulation the flow is turbulent in the regions behind the two fronts. Compared to the LGR simulation, the interfacial billows lose their coherence much more rapidly (over less than 2.5h behind the front), which results in a much faster decay of the large-scale content and turbulence intensity in the trailing regions of the flow. A slightly tilted, stably stratified interface layer develops away from the two fronts. The concentration profiles across this layer can be approximated by a hyperbolic tangent function. In the HGR simulation the energy budget shows that for t > 18h/ub the flow reaches a regime in which the total dissipation rate and the rates of change of the total potential and kinetic energies are constant in time. The second part of the paper focuses on the study of the transition of Boussinesq gravity currents with a small initial volume of the release to the buoyancy–inertia self-similar phase. When the existence of the back wall is communicated to the front, the front speed starts to decrease, and the current transitions to the buoyancy–inertia phase. Three high-resolution simulations are performed at Grashof numbers between 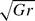= 3 × 104 and 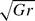= 9 × 104. Additionally, a calculation at a much higher Grashof number ( 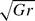= 106) is performed to understand the behaviour of a bottom-propagating current closer to the inviscid limit. The three-dimensional simulations correctly predict a front speed decrease proportional to t−α (the time t is measured from the release time) over the buoyancy–inertia phase, with the constant α approaching the theoretical value of 1/3 as the current approaches the inviscid limit. At Grashof numbers for which 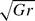> 3 × 104, the intensity of the turbulence in the near-wall region behind the front is large enough to induce the formation of a region containing streaks of low and high streamwise velocities. The streaks are present well into the buoyancy–inertia phase before the speed of the front decays below values at which the streaks can be sustained. The formation of the velocity streaks induces a streaky distribution of the bed friction velocity in the region immediately behind the front. This distribution becomes finer as the Grashof number increases. For simulations in which the only difference was the value of the Grashof number ( 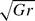= 4.7 × 104 versus 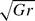= 106), analysis of the non-dimensional bed friction velocity distributions shows that the capacity of the gravity current to entrain sediment from the bed increases with the Grashof number. Past the later stages of the transition to the buoyancy–inertia phase, the temporal variations of the potential energy, the kinetic energy and the integral of the total dissipation rate are logarithmic.

Type
Papers
Information
Journal of Fluid Mechanics , Volume 635 , 25 September 2009 , pp. 361 - 388
Copyright
Copyright © Cambridge University Press 2009

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Benjamin, T. B. 1968 Gravity currents and related phenomena. J. Fluid Mech. 31, 209–248.CrossRefGoogle Scholar
Britter, R. E. & Simpson, J. E. 1978 Experiments on the dynamics of a gravity current head. J. Fluid Mech. 88, 223–240.CrossRefGoogle Scholar
Cantero, M. I., Lee, J. R., Balachandar, S. & Garcia, M. H. 2007 On the front velocity of gravity currents. J. Fluid Mech. 586, 1–39.CrossRefGoogle Scholar
Chang, K. S., Constantinescu, G. & Park, S-O. 2006 Analysis of the flow and mass transfer processes for the incompressible flow past an open cavity with a laminar and a fully turbulent incoming boundary layer. J. Fluid Mech. 561, 113–145.CrossRefGoogle Scholar
Chang, K. S., Constantinescu, G. & Park, S-O. 2007 The purging of a neutrally buoyant or a dense miscible contaminant from a rectangular cavity. Part 2. The case of an incoming fully turbulent overflow. J. Hydraul. Engng 133 (4), 373–385.CrossRefGoogle Scholar
Choi, S-U. & Garcia, M. H. 1995 Modeling of one-dimensional turbidity currents with a dissipative Galerkin finite-element method. J. Hydraul. Res. 33 (5), 623–648.CrossRefGoogle Scholar
Fanneløp, T. K. 1994 Fluid Mechanics for Industrial Safety and Environmental Protection. Elsevier.Google Scholar
Fannelop, T. K. & Waldman, G. D. 1972 Dynamics of oil slicks. AIAA J. 10, 506–510.CrossRefGoogle Scholar
Germano, M, Piomelli, U., Moin, P & Cabot, W. H. 1991 A dynamic subgrid-scale eddy viscosity model. Phys. Fluids A 3, 1760–1765.CrossRefGoogle Scholar
Hacker, J., Linden, P. F. & Dalziel, S. B. 1996 Mixing in lock-release gravity currents. Dyn. Atmos. Oceans 24, 183–195.CrossRefGoogle Scholar
Hallez, Y. & Magnaudet, J. 2008 Effects of channel geometry on buoyancy-driven mixing. Phys. Fluids 20, 053306.CrossRefGoogle Scholar
Hallworth, M. A., Huppert, H. E., Phillips, J. C. & Sparks, R. S. J. 1996 Entrainment into two-dimensional and axisymmetric turbulent gravity currents. J. Fluid Mech. 308, 289–311.CrossRefGoogle Scholar
Härtel, C., Carlsson, F. & Thunblom, M. 2000 a Analysis and direct numerical simulation of the flow at a gravity-current head. Part 2. The lobe-and-cleft instability. J. Fluid Mech. 418, 213–229.CrossRefGoogle Scholar
Härtel, C., Meiburg, E. & Necker, F. 2000 b Analysis and direct numerical simulation of the flow at a gravity-current head. Part 1. Flow topology and front speed for slip and no-slip boundaries. J. Fluid Mech. 418, 189–212.CrossRefGoogle Scholar
Hoult, D. P. 1972 Oil spreading on the sea. Annu. Rev. Fluid Mech. 4, 341–368.CrossRefGoogle Scholar
Huppert, H. 1982 The propagation of two-dimensional and axisymmetric viscous gravity currents over a rigid horizontal surface. J. Fluid. Mech. 121, 43–58.CrossRefGoogle Scholar
Huppert, H. & Simpson, J. E. 1980 The slumping of gravity currents. J. Fluid. Mech. 99, 785–799.CrossRefGoogle Scholar
Keller, J. J. & Chyou, Y.-P. 1991 On the hydraulic lock-exchange problem. J. Appl. Math. Phys. 42, 874–910.Google Scholar
Keulegan, G. H. 1957 An experimental study of the motion of saline water from locks into fresh water channels. Rep. 5168. US National Bureau of Standards.Google Scholar
Klemp, J. B., Rotunno, R. & Skamarock, W. C. 1997 On the propagation of internal bores. J. Fluid. Mech. 331, 81–106.CrossRefGoogle Scholar
Lilly, D. K. 1992 A proposed modification of the Germano subgrid scale closure method. Phys. Fluids A 4, 633–635.CrossRefGoogle Scholar
Mahesh, K., Constantinescu, G. & Moin, P. 2004 A numerical method for large eddy simulation in complex geometries, J. Comput. Physics 197, 215–240.CrossRefGoogle Scholar
Necker, F., Härtel, C., Kleiser, L. & Meiburg, E. 2005 Mixing and dissipation in particle-drive gravity currents. J. Fluid Mech. 545, 339–372.CrossRefGoogle Scholar
Ooi, S. K., Constantinescu, S. G. & Weber, L. 2007 a A numerical study of intrusive compositional gravity currents. Phys. Fluids 19, 076602. DOI: 10.1063/1.2750672.CrossRefGoogle Scholar
Ooi, S. K., Constantinescu, G. & Weber, L. J. 2007 b 2D Large Eddy Simulation of lock-exchange gravity current flows. ASCE J. Hydraulic Engineering 133, 361–372. DOI: 10.1061/(ASCE)0733-9429(2007)133.9(1037).CrossRefGoogle Scholar
Pierce, C. D. & Moin, P. 2001 Progress-variable approach for large-eddy simulation of turbulent cobustion. Rep. TF-80. Mechanical Engineering Department, Stanford University.Google Scholar
Pierce, C. D. & Moin, P. 2004 Progress-variable approach for large-eddy simulation of non-premixed turbulent combustion. J. Fluid Mech. 504, 73–97.CrossRefGoogle Scholar
Rottman, J. W. & Simpson, J. E. 1983 Gravity currents produced by instantaneous releases of a heavy fluid in a rectangular channel. J. Fluid Mech. 135, 95–110.CrossRefGoogle Scholar
Shin, J., Dalziel, S. & Linden, P. F. 2004 Gravity currents produced by lock exchange. J. Fluid Mech. 521, 1–34.CrossRefGoogle Scholar
Simpson, J. E. 1972 Effects of the lower boundary on the head of a gravity current. J. Fluid Mech. 53, 759–768.CrossRefGoogle Scholar
Simpson, J. E. 1997 Gravity Currents: In the Environment and the Laboratory, 2nd edn. Cambridge University Press.Google Scholar
Simpson, J. E. & Britter, R. E. 1979 The dynamics of the head of a gravity current advancing over a horizontal surface. J. Fluid Mech. 94, 477–495.CrossRefGoogle Scholar