Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-29T12:45:50.542Z Has data issue: false hasContentIssue false
  • English
  • Français

On the genesis of different regimes in canopy flows: a numerical investigation

Published online by Cambridge University Press:  20 March 2020

Alessandro Monti ,
Mohammad Omidyeganeh Open the ORCID record for Mohammad Omidyeganeh [Opens in a new window] ,
Bruno Eckhardt Open the ORCID record for Bruno Eckhardt [Opens in a new window]  and
Alfredo Pinelli Open the ORCID record for Alfredo Pinelli [Opens in a new window]
Alessandro Monti
Affiliation:
School of Mathematics, Computer Science and Engineering, City, University of London, LondonEC1V 0HB, UK
Mohammad Omidyeganeh
Affiliation:
School of Mathematics, Computer Science and Engineering, City, University of London, LondonEC1V 0HB, UK
Bruno Eckhardt
Affiliation:
Fachbereich Physik, Philipps-Universität Marburg, 35032Marburg, Germany
Alfredo Pinelli*
Affiliation:
School of Mathematics, Computer Science and Engineering, City, University of London, LondonEC1V 0HB, UK
*
†Email address for correspondence: alfredo.pinelli.1@city.ac.uk
Get access Rights & Permissions [Opens in a new window]

Abstract

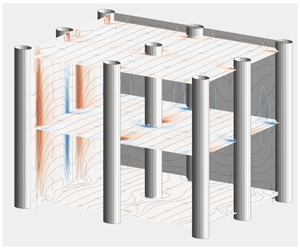
We have performed fully resolved simulations of turbulent flows over various submerged rigid canopies covering the wall of an open channel. All the numerical predictions have been obtained considering the same nominal bulk Reynolds number (i.e. $Re_{b}=U_{b}H/\unicode[STIX]{x1D708}=6000$, $H$ being the channel depth and $U_{b}$ the bulk velocity). The computations directly tackle the region occupied by the canopy by imposing the zero-velocity condition on every single stem, while the outer flow is dealt with a highly resolved large-eddy simulation. Four canopy configurations have been considered. All of them share the same in-plane solid fraction while the canopy to channel height ratios have been selected to be $h/H=(0.05,0.1,0.25,0.4)$. The lowest and the highest values lead to flow conditions approaching the two asymptotic states that in the literature are usually termed the sparse and dense regimes (see Nepf (Annu. Rev. Fluid Mech., vol. 44, 2012, pp. 123–142)). The other two $h/H$ selected ratios are representative of transitional regimes, a generic category that incorporates all the non-asymptotic states. While the interaction of a turbulent flow with a filamentous canopy in the two asymptotic conditions is relatively well understood, not much is known on the transitional flows and on the physical mechanisms that are responsible for the variations of flow regimes when the canopy solidity is changed. The effects of the latter on the flow developing in the intra-canopy region, on the outer flow and on their mutual interactions have been numerically explored and are reported in this work. By systematically varying the canopy height, we have unravelled the main character of the different regimes that are generated by the interplay between the outer flow structures, the emerging instabilities driven by the canopy drag and the interstitial flow between the canopy stems. The key role played by the relative positions of the inflection points of the mean velocity profile and the location of the virtual wall origin (as seen from the outer flow) is put forward and used to define a new condition to infer the canopy flow regime when the solidity is changed. Finally, the presence and the effects of an instability occurring close to the bed, nearby the interior inflectional point of the mean velocity profile is highlighted together with its consequences on the flow structure within the canopy region. To the best of our knowledge, this is the first time that the emergence of close-to-the-bed coherent structures induced by the inner inflection point is reported in the literature.

JFM classification

Turbulent Flows: Turbulence simulation Boundary Layers: Boundary layer structure
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 891 , 25 May 2020 , A9
Copyright
© The Author(s), 2020. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bailey, B. N. & Stoll, R. 2013 Turbulence in sparse, organized vegetative canopies: a large-eddy simulation study. Boundary-Layer Meteorol. 147 (3), 369–400.CrossRefGoogle Scholar
Bailey, B. N. & Stoll, R. 2016 The creation and evolution of coherent structures in plant canopy flows and their role in turbulent transport. J. Fluid Mech. 789, 425–460.CrossRefGoogle Scholar
Banyassady, R. & Piomelli, U. 2015 Interaction of inner and outer layers in plane and radial wall jets. J. Turbul. 16 (5), 460–483.CrossRefGoogle Scholar
Belcher, S. E., Jerram, N. & Hunt, J. C. R. 2003 Adjustment of a turbulent boundary layer to a canopy of roughness elements. J. Fluid Mech. 488, 369–398.CrossRefGoogle Scholar
Ben Meftah, M., De Serio, F. & Mossa, M. 2014 Hydrodynamic behavior in the outer shear layer of partly obstructed open channels. Phys. Fluids 26 (6), 065102.CrossRefGoogle Scholar
Ben Meftah, M. & Mossa, M. 2013 Prediction of channel flow characteristics through square arrays of emergent cylinders. Phys. Fluids 25 (4), 045102.CrossRefGoogle Scholar
Brücker, C. & Weidner, C. 2014 Influence of self-adaptive hairy flaps on the stall delay of an airfoil in ramp-up motion. J. Fluids Struct. 47, 31–40.CrossRefGoogle Scholar
Drazin, P. G. & Reid, W. H. 1981 Hydrodynamic Stability. Cambridge University Press.Google Scholar
Fadlun, E. A., Verzicco, R., Orlandi, P. & Mohd-Yusof, J. 2000 Combined immersed-boundary finite-difference methods for three-dimensional complex flow simulations. J. Comput. Phys. 161 (1), 35–60.CrossRefGoogle Scholar
Favier, J., Revell, A. & Pinelli, A. 2014 A lattice Boltzmann–immersed boundary method to simulate the fluid interaction with moving and slender flexible objects. J. Comput. Phys. 261, 145–161.CrossRefGoogle Scholar
Finnigan, J. J. 2000 Turbulence in plant canopies. Annu. Rev. Fluid Mech. 32 (1), 519–571.CrossRefGoogle Scholar
Finnigan, J. J., Shaw, R. H. & Patton, E. G. 2009 Turbulence structure above a vegetation canopy. J. Fluid Mech. 637, 387–424.CrossRefGoogle Scholar
García-Mayoral, R. & Jiménez, J. 2011 Hydrodynamic stability and breakdown of the viscous regime over riblets. J. Fluid Mech. 678, 317–347.CrossRefGoogle Scholar
Ghisalberti, M. & Nepf, H. M. 2002 Mixing layers and coherent structures in vegetated aquatic flows. J. Geophys. Res. 107 (C2), 3-1–3-11.CrossRefGoogle Scholar
Ghisalberti, M. & Nepf, H. M. 2004 The limited growth of vegetated shear layers. Water Resour. Res. 40 (7), W07502.Google Scholar
Hama, F. R. 1954 Boundary layer characteristics over smooth and rough surfaces. Trans. Soc. Nav. Archit. Mar. Engrs 62, 333.Google Scholar
Henson, V. E. & Yang, U. M. 2002 BoomerAMG: a parallel algebraic multigrid solver and preconditioner. Appl. Numer. Maths 41 (1), 155–177.CrossRefGoogle Scholar
Hoyas, S. & Jiménez, J. 2008 Reynolds number effects on the Reynolds-stress budgets in turbulent channels. Phys. Fluids 20 (10), 101511.CrossRefGoogle Scholar
Itoh, M., Iguchi, R., Yokota, K., Akino, N., Hino, R. & Kubo, S. 2006 Turbulent drag reduction by the seal fur surface. Phys. Fluids 18, 065102.CrossRefGoogle Scholar
Jiménez, J. 2004 Turbulent flows over rough walls. Annu. Rev. Fluid Mech. 36, 173–196.CrossRefGoogle Scholar
Jiménez, J. 2013 Near-wall turbulence. Phys. Fluids 25 (10), 101302.CrossRefGoogle Scholar
Jiménez, J. 2018 Coherent structures in wall-bounded turbulence. J. Fluid Mech. 842, 1–100.CrossRefGoogle Scholar
Jiménez, J., Uhlmann, M., Pinelli, A. & Kawahara, G. 2001 Turbulent shear flow over active and passive porous surfaces. J. Fluid Mech. 442, 89–117.CrossRefGoogle Scholar
Kim, J. & Moin, P. 1985 Application of a fractional-step method to incompressible Navier–Stokes equations. J. Comput. Phys. 59 (2), 308–323.CrossRefGoogle Scholar
Kim, J., Moin, P. & Moser, R. 1987 Turbulence statistics in fully developed channel flow at low Reynolds number. J. Fluid Mech. 177, 133–166.CrossRefGoogle Scholar
Leclercq, T. & de Langre, E. 2016 Drag reduction by elastic reconfiguration of non-uniform beams in non-uniform flows. J. Fluids Struct. 60, 114–129.CrossRefGoogle Scholar
Leonard, A. 1975 Energy cascade in large-eddy simulations of turbulent fluid flows. Adv. Geophys. 18, 237–248.CrossRefGoogle Scholar
Leonardi, S., Orlandi, P. & Antonia, R. A. 2007 Properties of d- and k-type roughness in a turbulent channel flow. Phys. Fluids 19 (12), 125101.CrossRefGoogle Scholar
Lightbody, A. F. & Nepf, H. M. 2006 Prediction of velocity profiles and longitudinal dispersion in salt marsh vegetation. Limnol. Oceanogr. 51 (1), 218–228.CrossRefGoogle Scholar
Lodish, H., Berk, A. & Kaiser, C. A. 2007 Molecular Cell Biology. W.H. Freeman & Co. Ltd.Google Scholar
Luhar, M., Rominger, J. & Nepf, H. M. 2008 Interaction between flow, transport and vegetation spatial structure. Environ. Fluid Mech. 8 (5–6), 423–439.CrossRefGoogle Scholar
Mars, R., Mathew, K. & Ho, G. 1999 The role of the submergent macrophyte Triglochin huegelii in domestic greywater treatment. Ecol. Engng 12 (1), 57–66.CrossRefGoogle Scholar
Monti, A., Omidyeganeh, M. & Pinelli, A. 2019 Large eddy simulation of of an open-channel flow bounded by a semi-dense rigid filamentous canopy: scaling and flow structure. Phys. Fluids 31, 065108.CrossRefGoogle Scholar
Nepf, H. M. 2012 Flow and transport in regions with aquatic vegetation. Annu. Rev. Fluid Mech. 44, 123–142.CrossRefGoogle Scholar
Nepf, H. M. & Vivoni, E. R. 2000 Flow structure in depth-limited, vegetated flow. J. Geophys. Res. 105 (C12), 28547–28557.CrossRefGoogle Scholar
Nezu, I. & Sanjou, M. 2008 Turburence structure and coherent motion in vegetated canopy open-channel flows. J. Hydro-Environ. Res. 2 (2), 62–90.CrossRefGoogle Scholar
Nikora, V., McEwan, I., McLean, S., Coleman, S., Pokrajac, D. & Walters, R. 2007 Double-averaging concept for rough-bed open-channel and overland flows: theoretical background. J. Hydraul. Engng 133 (8), 873–883.CrossRefGoogle Scholar
Nikuradse, J. 1933 Strömungsgestze in rauhen rohren. VDI Forsch. 361 (English translation in NACA-TM 1292 (1950)).Google Scholar
Omidyeganeh, M. & Piomelli, U. 2011 Large-eddy simulation of two-dimensional dunes in a steady, unidirectional flow. J. Turbul. 12, N42.CrossRefGoogle Scholar
Omidyeganeh, M. & Piomelli, U. 2013a Large-eddy simulation of three-dimensional dunes in a steady, unidirectional flow. Part 1. Turbulence statistics. J. Fluid Mech. 721, 454–483.CrossRefGoogle Scholar
Omidyeganeh, M. & Piomelli, U. 2013b Large-eddy simulation of three-dimensional dunes in a steady, unidirectional flow. Part 2. Flow structures. J. Fluid Mech. 734, 509–534.CrossRefGoogle Scholar
Perry, A. E., Schofield, W. H. & Joubert, P. N. 1969 Rough wall turbulent boundary layers. J. Fluid Mech. 37 (2), 383–413.CrossRefGoogle Scholar
Pinelli, A., Naqavi, I. Z., Piomelli, U. & Favier, J. 2010 Immersed-boundary methods for general finite-difference and finite-volume Navier–Stokes solvers. J. Comput. Phys. 229 (24), 9073–9091.CrossRefGoogle Scholar
Piomelli, U., Rouhi, A. & Geurts, B. J. 2015 A grid-independent length scale for large-eddy simulations. J. Fluid Mech. 766, 499–527.CrossRefGoogle Scholar
Poggi, D., Porporato, A., Ridolfi, L., Albertson, J. D. & Katul, G. G. 2004 The effect of vegetation density on canopy sub-layer turbulence. Boundary-Layer Meteorol. 111 (3), 565–587.CrossRefGoogle Scholar
Raupach, M. R., Finnigan, J. J. & Brunei, Y. 1996 Coherent eddies and turbulence in vegetation canopies: the mixing-layer analogy. Boundary-Layer Meteorol. 78 (3–4), 351–382.CrossRefGoogle Scholar
Raupach, M. R. & Shaw, R. H. 1982 Averaging procedures for flow within vegetation canopies. Boundary-Layer Meteorol. 22 (1), 79–90.CrossRefGoogle Scholar
Rhie, C. M. & Chow, W. L. 1983 Numerical study of the turbulent flow past an airfoil with trailing edge separation. AIAA J. 21 (11), 1525–1532.CrossRefGoogle Scholar
Rosti, M. E., Omidyeganeh, M. & Pinelli, A. 2016 Direct numerical simulation of the flow around an aerofoil in ramp-up motion. Phys. Fluids 28 (2), 025106.CrossRefGoogle Scholar
Rouhi, A., Piomelli, U. & Geurts, B. J. 2016 Dynamic subfilter-scale stress model for large-eddy simulations. Phys. Rev. F 1 (4), 044401.Google Scholar
Schlichting, H. 1936 Experimentelle untersuchungen zum rauhigkeitsproblem. Arch. Appl. Mech. 7 (1), 1–34.Google Scholar
Schultz, M. P. & Flack, K. A. 2009 Turbulent boundary layers on a systematically varied rough wall. Phys. Fluids 21 (1), 015104.CrossRefGoogle Scholar
Scotti, A. 2006 Direct numerical simulation of turbulent channel flows with boundary roughened with virtual sandpaper. Phys. Fluids 18 (3), 031701.CrossRefGoogle Scholar
Sharma, A. & García-Mayoral, R.2018 Scaling and modelling of turbulent flow over a sparse canopy. arXiv:1810.10028.CrossRefGoogle Scholar
Shimizu, Y., Tsujimoto, T., Nakagawa, H. & Kitamura, T. 1991 Experimental study on flow over rigid vegetation simulated by cylinders with equi-spacing. Doboku Gakkai Ronbunshu 1991 (438), 31–40.CrossRefGoogle Scholar
Tani, I. 1987 Turbulent boundary layer development over rough surfaces. In Perspectives in Turbulence Studies, pp. 223–249. Springer.CrossRefGoogle Scholar
Tuerke, F. & Jiménez, J. 2013 Simulations of turbulent channels with prescribed velocity profiles. J. Fluid Mech. 723, 587–603.CrossRefGoogle Scholar
Webb, R. L., Eckert, E. R. G. & Goldstein, R. J. 1971 Heat transfer and friction in tubes with repeated-rib roughness. Intl J. Heat Mass Transfer 14 (4), 601–617.CrossRefGoogle Scholar
Wilcock, R. J., Champion, P. D., Nagels, J. W. & Croker, G. F. 1999 The influence of aquatic macrophytes on the hydraulic and physico-chemical properties of a New Zealand lowland stream. Hydrobiologia 416, 203–214.CrossRefGoogle Scholar
Yuan, J. & Piomelli, U. 2014 Roughness effects on the Reynolds stress budgets in near-wall turbulence. J. Fluid Mech. 760, R1.CrossRefGoogle Scholar