Hostname: page-component-78c5997874-m6dg7 Total loading time: 0 Render date: 2024-11-19T13:31:23.200Z Has data issue: false hasContentIssue false
  • English
  • Français

On the global nonlinear instability of the rotating-disk flow over a finite domain

Published online by Cambridge University Press:  22 August 2016

E. Appelquist ,
P. Schlatter ,
P. H. Alfredsson  and
R. J. Lingwood
E. Appelquist*
Affiliation:
Linné FLOW Centre, KTH Mechanics, SE-100 44 Stockholm, Sweden Swedish e-Science Research Centre (SeRC), SE-100 44 Stockholm, Sweden
P. Schlatter*
Affiliation:
Linné FLOW Centre, KTH Mechanics, SE-100 44 Stockholm, Sweden Swedish e-Science Research Centre (SeRC), SE-100 44 Stockholm, Sweden
P. H. Alfredsson
Affiliation:
Linné FLOW Centre, KTH Mechanics, SE-100 44 Stockholm, Sweden
R. J. Lingwood
Affiliation:
Linné FLOW Centre, KTH Mechanics, SE-100 44 Stockholm, Sweden Centre for Simulation and Applied Mechanics, School of Engineering and Materials Science, Queen Mary University of London, Mile End Road, London E1 4NS, UK
*
†Email addresses for correspondence: ellinor@mech.kth.se, pschlatt@mech.kth.se
†Email addresses for correspondence: ellinor@mech.kth.se, pschlatt@mech.kth.se
Get access Rights & Permissions [Opens in a new window]

Abstract

Direct numerical simulations based on the incompressible nonlinear Navier–Stokes equations of the flow over the surface of a rotating disk have been conducted. An impulsive disturbance was introduced and its development as it travelled radially outwards and ultimately transitioned to turbulence has been analysed. Of particular interest was whether the nonlinear stability is related to the linear stability properties. Specifically three disk-edge conditions were considered; (i) a sponge region forcing the flow back to laminar flow, (ii) a disk edge, where the disk was assumed to be infinitely thin and (iii) a physically realistic disk edge of finite thickness. This work expands on the linear simulations presented by Appelquist et al. (J. Fluid. Mech., vol. 765, 2015, pp. 612–631), where, for case (i), this configuration was shown to be globally linearly unstable when the sponge region effectively models the influence of the turbulence on the flow field. In contrast, case (ii) was mentioned there to be linearly globally stable, and here, where nonlinearity is included, it is shown that both cases (ii) and (iii) are nonlinearly globally unstable. The simulations show that the flow can be globally linearly stable if the linear wavepacket has a positive front velocity. However, in the same flow field, a nonlinear global instability can emerge, which is shown to depend on the outer turbulent region generating a linear inward-travelling mode that sustains a transition front within the domain. 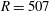The results show that the front position does not approach the critical Reynolds number for the local absolute instability, $R=507$. Instead, the front approaches 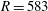$R=583$ and both the temporal frequency and spatial growth rate correspond to a global mode originating at this position.

JFM classification

Instability: Absolute/convective instability Boundary Layers: Boundary layer stability Geophysical and Geological Flows: Rotating flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 803 , 25 September 2016 , pp. 332 - 355
Check for updates
Copyright
© 2016 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Appelquist, E.2014 Direct numerical simulations of the rotating-disk boundary-layer flow. Licentiate thesis, Royal Institute of Technology, KTH Mechanics, ISBN: 978-91-7595-202-4.Google Scholar
Appelquist, E., Schlatter, P., Alfredsson, P. H. & Lingwood, R. J. 2015a Global linear instability of the rotating-disk flow investigated through simulations. J. Fluid Mech. 765, 612–631.CrossRefGoogle Scholar
Appelquist, E., Schlatter, P., Alfredsson, P. H. & Lingwood, R. J. 2015b Investigation of the global instability of the rotating-disk boundary layer. Proc. IUTAM 14, 321–328.Google Scholar
Chomaz, J.-M. 2004 Transition to turbulence in open flows: what linear and fully nonlinear local and global theories tell us. Eur. J. Mech. (B/Fluids) 23, 385–399.CrossRefGoogle Scholar
Davies, C. & Carpenter, P. W. 2003 Global behaviour corresponding to the absolute instability of the rotating-disc boundary layer. J. Fluid Mech. 486, 287–329.Google Scholar
Davies, C., Thomas, C. & Carpenter, P. W. 2007 Global stability of the rotating-disk boundary layer. J. Engng Maths 57, 219–236.Google Scholar
Fischer, P. F., Lottes, J. W. & Kerkemeier, S. G.2012 Nek5000 Web page. http://nek5000.mcs.anl.gov.Google Scholar
Gregory, N., Stuart, J. T. & Walker, W. S. 1955 On the stability of three-dimensional boundary layers with application to the flow due to a rotating disk. Phil. Trans. R. Soc. Lond. A 248, 155–199.Google Scholar
Healey, J. J. 2010 Model for unstable global modes in the rotating-disk boundary layer. J. Fluid Mech. 663, 148–159.CrossRefGoogle Scholar
Imayama, S., Alfredsson, P. H. & Lingwood, R. J. 2012 A new way to describe the transition characteristics of a rotating-disk boundary-layer flow. Phys. Fluids 24, 031701.Google Scholar
Imayama, S., Alfredsson, P. H. & Lingwood, R. J. 2013 An experimental study of edge effects on rotating-disk transition. J. Fluid Mech. 716, 638–657.CrossRefGoogle Scholar
Imayama, S., Alfredsson, P. H. & Lingwood, R. J. 2014 On the laminar-turbulent transition of the rotating-disk flow – the role of absolute instability. J. Fluid Mech. 745, 132–163.Google Scholar
Imayama, S., Alfredsson, P. H. & Lingwood, R. J. 2016 Experimental study of rotating-disk boundary-layer flow with surface roughness. J. Fluid Mech. 786, 5–28.Google Scholar
von Kármán, T. 1921 Über laminare und turbulente Reibung. Z. Angew. Math. Mech. 1, 232–252.Google Scholar
Karniadakis, G. E., Israeli, M. & Orszag, S. A. 1991 High-order splitting methods for the incompressible Navier–Stokes equations. J. Comput. Phys. 97, 414–443.CrossRefGoogle Scholar
Kobayashi, R., Kohama, Y. & Takamadate, Ch. 1980 Spiral vortices in boundary layer transition regime on a rotating disk. Acta Mechanica 35, 71–82.CrossRefGoogle Scholar
Lee, K., Nishio, Y., Izawa, S. & Fukunishi, Y. 2014 Numerical study of absolute instability on a rotating disk flow. In 67th Annual Meeting of the APS Division of Fluid Dynamics, vol. 59. APS Bulletin. http://meetings.aps.org/link/BAPS.2014.DFD.D21.8.Google Scholar
Lingwood, R. J. 1995 Absolute instability of the boundary layer on a rotating disk. J. Fluid Mech. 299, 17–33.CrossRefGoogle Scholar
Lingwood, R. J. 1996 An experimental study of absolute instability of the rotating-disk boundary-layer flow. J. Fluid Mech. 314, 373–405.Google Scholar
Lingwood, R. J. 1997 On the effects of suction and injection on the absolute instability of the rotating-disk boundary layer. Phys. Fluids 9, 1317–1328.CrossRefGoogle Scholar
Mack, L. M.1985 The wave pattern produced by a point source on a rotating disk. AIAA Paper 85-0490.CrossRefGoogle Scholar
Malik, M. R. 1986 The neutral curve for stationary disturbances in rotating-disk flow. J. Fluid Mech. 164, 275–287.Google Scholar
Malik, M. R., Wilkinson, S. P. & Orszag, S. A. 1981 Instability and transition in rotating disk flow. AIAA J. 19, 1131–1138.CrossRefGoogle Scholar
Othman, H. & Corke, T. C. 2006 Experimental investigation of absolute instability of a rotating-disk boundary layer. J. Fluid Mech. 565, 63–94.Google Scholar
Patera, A. T. 1984 A spectral element method for fluid dynamics: Laminar flow in a channel expansion. J. Comput. Phys. 54, 468–488.CrossRefGoogle Scholar
Pier, B. 2003 Finite-amplitude crossflow vortices, secondary instability and transition in the rotating-disk boundary layer. J. Fluid Mech. 487, 315–343.Google Scholar
Pier, B. 2007 Primary crossflow vortices, secondary absolute instabilities and their control in the rotating-disk boundary layer. J.  Engng Maths 57, 237–251.Google Scholar
Pier, B. 2013 Transition near the edge of a rotating disk. J. Fluid Mech. 737, R1.Google Scholar
Pier, B. & Huerre, P. 2001 Nonlinear synchronization in open flows. J. Fluids Struct. 15, 471–480.Google Scholar
Pier, B., Huerre, P., Chomaz, J.-M. & Couairon, A. 1998 Steep nonlinear global modes in spatially developing media. Phys. Fluids 10, 2433–2435.CrossRefGoogle Scholar
Siddiqui, M. E., Mukund, V., Scott, J. & Pier, B. 2013 Experimental characterization of transition region in rotating-disk boundary layer. Phys. Fluids 25, 573–576.Google Scholar
Viaud, B., Serre, E. & Chomaz, J.-M. 2008 The elephant mode between two rotating disks. J. Fluid Mech. 598, 451–464.CrossRefGoogle Scholar
Viaud, B., Serre, E. & Chomaz, J.-M. 2011 Transition to turbulence through steep global-modes cascade in an open rotating cavity. J. Fluid Mech. 688, 493–506.CrossRefGoogle Scholar
Wilkinson, S. & Malik, M. R. 1985 Stability experiments in the flow over a rotating disk. AIAA J. 23, 588–595.CrossRefGoogle Scholar