Hostname: page-component-78c5997874-fbnjt Total loading time: 0 Render date: 2024-11-17T15:15:36.512Z Has data issue: false hasContentIssue false
  • English
  • Français

On the mechanism of trailing vortex wandering

Published online by Cambridge University Press:  19 July 2016

Adam M. Edstrand ,
Timothy B. Davis ,
Peter J. Schmid ,
Kunihiko Taira  and
Louis N. Cattafesta III
Adam M. Edstrand*
Affiliation:
Department of Mechanical Engineering, Florida Center for Advanced Aero-Propulsion, 2003 Levy Ave., Florida State University, Tallahassee, FL 32310, USA
Timothy B. Davis
Affiliation:
Department of Mechanical Engineering, Florida Center for Advanced Aero-Propulsion, 2003 Levy Ave., Florida State University, Tallahassee, FL 32310, USA
Peter J. Schmid
Affiliation:
Department of Mathematics, Imperial College London, London SW7 2AZ, UK
Kunihiko Taira
Affiliation:
Department of Mechanical Engineering, Florida Center for Advanced Aero-Propulsion, 2003 Levy Ave., Florida State University, Tallahassee, FL 32310, USA
Louis N. Cattafesta III
Affiliation:
Department of Mechanical Engineering, Florida Center for Advanced Aero-Propulsion, 2003 Levy Ave., Florida State University, Tallahassee, FL 32310, USA
*
†Email address for correspondence: aedstrand@fsu.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

The mechanism of trailing vortex wandering has long been debated and is often attributed to either wind-tunnel effects or an instability. Using particle image velocimetry data obtained in the wake of a NACA0012 airfoil, we remove the effect of wandering from the measured velocity field and, through a triple decomposition, recover the coherent wandering motion. 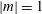Based on this wandering motion, the most energetic structures are computed using the proper orthogonal decomposition (POD) and exhibit a helical mode with an azimuthal wavenumber of $|m|=1$ whose kinetic energy grows monotonically in the downstream direction. To investigate the nature of the vortex wandering, we perform a spatial stability analysis of a matched Batchelor vortex. The primary stability mode is found to be marginally stable and nearly identical in both size and structure to the leading POD mode. The strikingly similar structure, coupled with the measured energy growth, supports the proposition that the vortex wandering is the result of an instability. We conclude that the cause of the wandering is the non-zero radial velocity of the 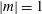$|m|=1$ mode on the vortex centreline, which acts to transversely displace the trailing vortex, as observed in experiments. However, the marginal nature of the stability mode prevents a definitive conclusion regarding the specific type of instability.

JFM classification

Vortex Flows: Vortex dynamics Vortex Flows: Vortex instability Wakes/Jets: Wakes
Type
Rapids
Information
Journal of Fluid Mechanics , Volume 801 , 25 August 2016 , R1
Check for updates
Copyright
© 2016 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bailey, S. C. C. & Tavoularis, S. 2008 Measurements of the velocity field of a wing-tip vortex, wandering in grid turbulence. J. Fluid Mech. 601, 281–315.Google Scholar
Baker, G. R., Barker, S. J., Bofah, K. K. & Saffman, P. G. 1974 Laser anemometer measurements of trailing vortices in water. J. Fluid Mech. 65 (2), 325–336.Google Scholar
Batchelor, G. K. 1964 Axial flow in trailing line vortices. J. Fluid Mech. 20 (4), 645–658.CrossRefGoogle Scholar
Beresh, S. J., Henfling, J. F. & Spillers, R. W. 2010 Meander of a fin trailing vortex and the origin of its turbulence. Exp. Fluids 49 (3), 599–611.CrossRefGoogle Scholar
Corsiglia, V. R., Schwind, R. G. & Chigier, N. A. 1973 Rapid scanning, three-dimensional hot-wire anemometer surveys of wing-tip vortices. J. Aircraft 10 (12), 752–757.Google Scholar
Deem, E., Edstrand, A., Reger, R., Pascioni, K. & Cattafesta, L. 2013 Deconvolution correction for wandering in wingtip vortex flowfield data. J. Fluid Sci. Technol. 8 (2), 219–232.Google Scholar
Devenport, W. J., Rife, M. C., Liapis, S. I. & Follin, G. J. 1996 The structure and development of a wing-tip vortex. J. Fluid Mech. 312, 67–106.Google Scholar
Fontane, J., Brancher, P. & Fabre, D. 2008 Stochastic forcing of the Lamb–Oseen vortex. J. Fluid Mech. 613, 233–254.CrossRefGoogle Scholar
Hein, S. & Theofilis, V. 2004 On instability characteristics of isolated vortices and models of trailing vortex systems. Comput. Fluids 33 (5–6), 741–753.Google Scholar
Heyes, A. L., Jones, R. F. & Smith, D. A. R. 2004 Wandering of wing-tip vortices. In International Symposia on Applications of Laser Techniques to Fluid Mechanics, Lisbon, Portugal, pp. 1–20.Google Scholar
Jacquin, L., Fabre, D., Geffroy, P. & Coustols, E.2001 The properties of a transport aircraft wake in the extended near field: an experimental study. AIAA Paper 2001-1038.CrossRefGoogle Scholar
Mathew, J., Bahr, C., Sheplak, M., Carroll, B. & Cattafesta, L.2005 Design, fabrication and characterization of an anechoic wind tunnel facility. AIAA Paper 2005-3052.Google Scholar
Mohseni, K. & Colonius, T. 2000 Numerical treatment of polar coordinate singularities. J. Comput. Phys. 157 (2), 787–795.Google Scholar
Paredes, P.2014 Advances in global instability computations: from incompressible to hypersonic flows. PhD thesis, Univ. Politécnica de Madrid.Google Scholar
Reynolds, W. C. & Hussain, A. K. M. F. 1972 The mechanics of an organized wave in turbulent shear flow. Part 3. Theoretical models and comparisons with experiments. J. Fluid Mech. 54 (2), 263–288.CrossRefGoogle Scholar
Rokhsaz, K., Foster, S. R. & Miller, L. S. 2000 Exploratory study of aircraft wake vortex filaments in a water tunnel. J. Aircraft 37 (6), 1022–1027.Google Scholar
Schmid, P. & Henningson, D. 2001 Stability and Transition in Shear Flows. Springer.CrossRefGoogle Scholar
Sirovich, L. 1987 Turbulence and the dynamics of coherent structures. Part 1: coherent structures. Q. Appl. Maths 45 (3), 561–571.Google Scholar