Hostname: page-component-586b7cd67f-2plfb Total loading time: 0 Render date: 2024-11-25T18:51:12.318Z Has data issue: false hasContentIssue false
  • English
  • Français

On the self-sustained nature of large-scale motions in turbulent Couette flow

Published online by Cambridge University Press:  09 October 2015

Subhandu Rawat ,
Carlo Cossu Open the ORCID record for Carlo Cossu [Opens in a new window] ,
Yongyun Hwang  and
François Rincon
Subhandu Rawat
Affiliation:
Institut de Mécanique des Fluides de Toulouse (IMFT), CNRS – Université de Toulouse, Allée du Pr. Camille Soula, F-31400 Toulouse, France
Carlo Cossu*
Affiliation:
Institut de Mécanique des Fluides de Toulouse (IMFT), CNRS – Université de Toulouse, Allée du Pr. Camille Soula, F-31400 Toulouse, France
Yongyun Hwang
Affiliation:
Department of Aeronautics, Imperial College, South Kensington, London SW7 2AZ, UK
François Rincon
Affiliation:
Université de Toulouse; UPS-OMP; IRAP; Toulouse, France CNRS; IRAP; 14 avenue Edouard Belin, F-31400 Toulouse, France
*
†Email address for correspondence: carlo.cossu@imft.fr
Get access Rights & Permissions [Opens in a new window]

Abstract

Large-scale motions in wall-bounded turbulent flows are frequently interpreted as resulting from an aggregation process of smaller-scale structures. Here, we explore the alternative possibility that such large-scale motions are themselves self-sustained and do not draw their energy from smaller-scale turbulent motions activated in buffer layers. 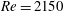To this end, it is first shown that large-scale motions in turbulent Couette flow at $Re=2150$ self-sustain, even when active processes at smaller scales are artificially quenched by increasing the Smagorinsky constant 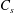$C_{s}$ in large-eddy simulations (LES). These results are in agreement with earlier results on pressure-driven turbulent channel flows. We further investigate the nature of the large-scale coherent motions by computing upper- and lower-branch nonlinear steady solutions of the filtered (LES) equations with a Newton–Krylov solver, and find that they are connected by a saddle–node bifurcation at large values of 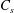$C_{s}$. Upper-branch solutions for the filtered large-scale motions are computed for Reynolds numbers up to 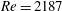$Re=2187$ using specific paths in the 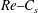$Re{-}C_{s}$ parameter plane and compared to large-scale coherent motions. Continuation to 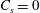$C_{s}=0$ reveals that these large-scale steady solutions of the filtered equations are connected to the Nagata–Clever–Busse–Waleffe branch of steady solutions of the Navier–Stokes equations. In contrast, we find it impossible to connect the latter to buffer-layer motions through a continuation to higher Reynolds numbers in minimal flow units.

JFM classification

Nonlinear Dynamical Systems: Nonlinear Dynamical Systems Instability: Transition to turbulence Turbulent Flows: Turbulent Flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 782 , 10 November 2015 , pp. 515 - 540
Check for updates
Copyright
© 2015 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Adrian, R. J. 2007 Hairpin vortex organization in wall turbulence. Phys. Fluids 19, 041301.CrossRefGoogle Scholar
Adrian, R. J., Meinhart, C. D. & Tomkins, C. D. 2000 Vortex organization in the outer region of the turbulent boundary layer. J. Fluid Mech. 422, 1–54.Google Scholar
del Álamo, J. C. & Jiménez, J. 2003 Spectra of the very large anisotropic scales in turbulent channels. Phys. Fluids 15, L41.CrossRefGoogle Scholar
del Álamo, J. C. & Jiménez, J. 2006 Linear energy amplification in turbulent channels. J. Fluid Mech. 559, 205–213.Google Scholar
Artuso, R., Aurell, E. & Cvitanovic, P. 1990 Recycling of strange sets. Part I: cycle expansions. Nonlinearity 3, 325–359.Google Scholar
Avsarkisov, V., Hoyas, S., Oberlack, M. & Garcia-Galache, J. P. 2014 Turbulent plane Couette flow at moderately high Reynolds number. J. Fluid Mech. 751, R1–1–R2–9.CrossRefGoogle Scholar
Balay, S., Brown, J., Buschelman, K., Gropp, W. D., Kaushik, D., Knepley, M. G., McInnes, L. C., Smith, B. F. & Zhang, H.2011. PETSc Web page. http://www.mcs.anl.gov/petsc.Google Scholar
Bewley, T. R., Moin, P. & Temam, R. 2001 DNS-based predictive control of turbulence: an optimal benchmark for feedback algorithms. J. Fluid Mech. 447, 179–225.CrossRefGoogle Scholar
Blackwelder, R. F. & Kovasznay, L. S. G. 1972 Time scales and correlations in a turbulent boundary layer. Phys. Fluids 15, 1545–1554.CrossRefGoogle Scholar
Chandler, G. J. & Kerswell, R. R. 2013 Invariant recurrent solutions embedded in a turbulent two-dimensional Kolmogorov flow. J. Fluid Mech. 722, 554–595.Google Scholar
Clever, R. M. & Busse, F. H. 1997 Tertiary and quaternary solutions for plane Couette flow. J. Fluid Mech. 344, 137–153.Google Scholar
Clever, R. M. & Busse, F. H. 1992 Three-dimensional convection in a horizontal fluid layer subjected to a constant shear. J. Fluid Mech. 234, 511–527.Google Scholar
Corrsin, S. & Kistler, A. L. 1954 The free-stream boundaries of turbulent flows. NACA Tech. Rep. 3133, 120–130.Google Scholar
Cossu, C., Brandt, L., Bagheri, S. & Henningson, D. S. 2011 Secondary threshold amplitudes for sinuous streak breakdown. Phys. Fluids 23, 074103.Google Scholar
Cossu, C., Pujals, G. & Depardon, S. 2009 Optimal transient growth and very large scale structures in turbulent boundary layers. J. Fluid Mech. 619, 79–94.CrossRefGoogle Scholar
Deardorff, P. E. 1970 A numerical study of three-dimensional turbulent channel flow at large Reynolds numbers. J. Fluid Mech. 41, 453–480.CrossRefGoogle Scholar
Dennis, D. J. C. & Nickels, T. B. 2011 Experimental measurement of large-scale three-dimensional structures in a turbulent boundary layer. Part 2. Long structures. J. Fluid Mech. 673, 218–244.CrossRefGoogle Scholar
Eitel-Amor, G., Örlü, R., Schlatter, P. & Flores, O. 2015 Hairpin vortices in turbulent boundary layers. Phys. Fluids 27 (2), 025108.Google Scholar
Ellingsen, T. & Palm, E. 1975 Stability of linear flow. Phys. Fluids 18, 487–488.Google Scholar
Falco, R. E. 1977 Coherent motions in the outer region of turbulent boundary layers. Phys. Fluids 20, S124–S132.CrossRefGoogle Scholar
Flores, O. & Jiménez, J. 2006 Effect of wall-boundary disturbances on turbulent channel flows. J. Fluid Mech. 566, 357–376.Google Scholar
Flores, O. & Jiménez, J. 2010 Hierarchy of minimal flow units in the logarithmic layer. Phys. Fluids 22, 071704.CrossRefGoogle Scholar
Flores, O., Jiménez, J. & del Álamo, J. C. 2007 Vorticity organization in the outer layer of turbulent channels with disturbed walls. J. Fluid Mech. 591, 145–154.Google Scholar
Gibson, J. F., Halcrow, J. & Cvitanovic, P. 2008 Visualizing the geometry of state space in plane Couette flow. J. Fluid Mech. 611, 107–130.Google Scholar
Guala, M., Hommema, S. E. & Adrian, R. J. 2006 Large-scale and very-large-scale motions in turbulent pipe flow. J. Fluid Mech. 554, 521–541.Google Scholar
Hamilton, J. M., Kim, J. & Waleffe, F. 1995 Regeneration mechanisms of near-wall turbulence structures. J. Fluid Mech 287, 317–348.CrossRefGoogle Scholar
Härtel, C. & Kleiser, L. 1998 Analysis and modelling of subgrid-scale motions in near-wall turbulence. J. Fluid Mech. 356, 327–352.Google Scholar
Head, M. R. & Bandyopadhay, P. 1981 New aspects of turbulent boundary-layer structure. J. Fluid Mech. 107, 297–338.Google Scholar
Herault, J., Rincon, F., Cossu, C., Lesur, G., Ogilvie, G. I. & Longaretti, P. Y. 2011 Periodic magnetorotational dynamo action as a prototype of nonlinear magnetic field generation in shear flows. Phys. Rev. E 84, 036321.Google Scholar
Hutchins, N. & Marusic, I. 2007a Evidence of very long meandering features in the logarithmic region of turbulent boundary layers. J. Fluid Mech. 579, 1–28.Google Scholar
Hutchins, N. & Marusic, I. 2007b Large-scale influences in near-wall turbulence. Phil. Trans. R. Soc. Lond. A 365, 647–664.Google Scholar
Hwang, Y. 2013 Near-wall turbulent fluctuations in the absence of wide outer motions. J. Fluid Mech. 723, 264–288.Google Scholar
Hwang, Y. 2015 Statistical structure of self-sustaining attached eddies in turbulent channel flow. J. Fluid Mech. 767, 254–289.Google Scholar
Hwang, Y. & Cossu, C. 2010a Amplification of coherent streaks in the turbulent Couette flow: an input-output analysis at low Reynolds number. J. Fluid Mech. 643, 333–348.CrossRefGoogle Scholar
Hwang, Y. & Cossu, C. 2010b Linear non-normal energy amplification of harmonic and stochastic forcing in turbulent channel flow. J. Fluid Mech. 664, 51–73.Google Scholar
Hwang, Y. & Cossu, C. 2010c Self-sustained process at large scales in turbulent channel flow. Phys. Rev. Lett. 105 (4), 044505.Google Scholar
Hwang, Y. & Cossu, C. 2011 Self-sustained processes in the logarithmic layer of turbulent channel flows. Phys. Fluids 23, 061702.Google Scholar
Itano, T. & Toh, S. 2001 The dynamics of bursting process in wall turbulence. J. Phys. Soc. Japan 70, 703–716.Google Scholar
Jeong, J., Hussain, F., Schoppa, W. & Kim, J. 1997 Coherent structures near the wall in a turbulent channel flow. J. Fluid Mech. 332, 185–214.Google Scholar
Jiménez, J. & Moin, P. 1991 The minimal flow unit in near-wall turbulence. J. Fluid Mech. 225, 213–240.Google Scholar
Kawahara, G. & Kida, S. 2001 Periodic motion embedded in plane Couette turbulence: regeneration cycle and burst. J. Fluid Mech. 449, 291–300.Google Scholar
Kerswell, R. R. & Tutty, O. R. 2007 Recurrence of travelling waves in transitional pipe flow. J. Fluid Mech. 584, 69–102.Google Scholar
Kim, J., Moin, P. & Moser, R. 1987 Turbulence statistics in fully developed channel flow at low Reynolds number. J. Fluid Mech. 177, 133–166.Google Scholar
Kim, K. C. & Adrian, R. 1999 Very large-scale motion in the outer layer. Phys. Fluids 11 (2), 417–422.Google Scholar
Kim, W. W & Menon, S. 1999 An unsteady incompressible Navier–Stokes solver for large eddy simulation of turbulent flows. Intl J. Numer. Meth. Fluids 31, 983–1017.Google Scholar
Kitoh, O., Nakabayashi, K. & Nishimura, F. 2005 Experimental study on mean velocity and turbulence characteristics of plane Couette flow: low-Reynolds-number effects and large longitudinal vortical structures. J. Fluid Mech. 539, 199–227.Google Scholar
Kitoh, O. & Umeki, M. 2008 Experimental study on large-scale streak structure in the core region of turbulent plane Couette flow. Phys. Fluids 20, 025107.Google Scholar
Kline, S. J., Reynolds, W. C., Schraub, F. A. & Runstadler, P. W. 1967 The structure of turbulent boundary layers. J. Fluid Mech. 30, 741–773.Google Scholar
Komminaho, J., Lundbladh, A. & Johansson, A. V. 1996 Very large structures in plane turbulent Couette flow. J. Fluid Mech. 320, 259–285.Google Scholar
Kovasznay, L. S. G., Kibens, V. & Blackwelder, R. F. 1970 Large-scale motion in the intermittent region of a turbulent boundary layer. J. Fluid Mech. 41, 283–325.Google Scholar
Landahl, M. T. 1980 A note on an algebraic instability of inviscid parallel shear flows. J. Fluid Mech. 98, 243–251.CrossRefGoogle Scholar
Landahl, M. T. 1990 On sublayer streaks. J. Fluid Mech. 212, 593–614.Google Scholar
Lee, M. J. & Kim, J. 1991 The structure of turbulence in a simulated plane Couette flow. In Proceedings of the 8th Symposium on Turbulent Shear Flow, Technical University of Munich, September 9–11, pp. 5.3.1–5.3.6.Google Scholar
Mason, P. J. & Callen, N. S. 1986 On the magnitude of the subgrid-scale eddy coefficient in large-eddy simulations of turbulent channel flow. J. Fluid Mech. 162, 439–462.Google Scholar
Mathis, R., Hutchins, N. & Marusic, I. 2009 Large-scale amplitude modulation of the small-scale structures in turbulent boudnary layers. J. Fluid Mech. 628, 311–337.Google Scholar
Mathis, R., Hutchins, N. & Marusic, I. 2011 A predictive inner–outer model for streamwise turbulence statistics in wall-bounded flows. J. Fluid Mech. 681, 537–566.CrossRefGoogle Scholar
Moffatt, H. K. 1967 The interaction of turbulence with strong wind shear. In Proceedings of the URSI-IUGG Colloquium on Atomspheric Turbulence and Radio Wave Propag (ed. Yaglom, A. M. & Tatarsky, V. I.), pp. 139–154. Nauka.Google Scholar
Nagata, M. 1990 Three-dimensional finite-amplitude solutions in plane Couette flow: bifurcation from infinity. J. Fluid Mech. 217, 519–527.Google Scholar
Park, J., Hwang, Y. & Cossu, C. 2011 On the stability of large-scale streaks in turbulent Couette and Poiseulle flows. C. R. Méc. 339, 1–5.Google Scholar
Perry, A. E. & Chong, M. S. 1982 On the mechanism of turbulence. J. Fluid Mech. 119, 173–217.Google Scholar
Pirozzoli, S., Bernardini, M. & Orlandi, P. 2014 Turbulence statistics in Couette flow at high Reynolds number. J. Fluid Mech. 758, 327–343.Google Scholar
Pope, S. B. 2000 Turbulent Flows. Cambridge University Press.Google Scholar
Pujals, G., Cossu, C. & Depardon, S. 2010 Forcing large-scale coherent streaks in a zero pressure gradient turbulent boundary layer. J. Turbul. 11 (25), 1–13.Google Scholar
Pujals, G., García-Villalba, M., Cossu, C. & Depardon, S. 2009 A note on optimal transient growth in turbulent channel flows. Phys. Fluids 21, 015109.Google Scholar
Rawat, S.2014 Coherent dynamics of large-scale turbulent motions. PhD thesis, Université de Toulouse.Google Scholar
Reddy, S. C., Schmid, P. J., Baggett, J. S. & Henningson, D. S. 1998 On the stability of streamwise streaks and transition thresholds in plane channel flows. J. Fluid Mech. 365, 269–303.Google Scholar
Reynolds, W. C. & Hussain, A. K. M. F. 1972 The mechanics of an organized wave in turbulent shear flow. Part 3. Theoretical models and comparisons with experiments. J. Fluid Mech. 54 (02), 263–288.Google Scholar
Rincon, F., Ogilvie, G. I. & Proctor, M. R. E. 2007a Self-sustaining nonlinear dynamo process in keplerian shear flows. Phys. Rev. Lett. 98 (25), 254502.Google Scholar
Rincon, F., Ogilvie, G. I. & Cossu, C. 2007b On self-sustaining processes in Rayleigh-stable rotating plane Couette flows and subcritical transition to turbulence in accretion disks. Astron. Astrophys. 463, 817–832.Google Scholar
Rincon, F., Ogilvie, G. I., Proctor, M. R. E. & Cossu, C. 2008 Subcritical dynamos in shear flows. Astron. Nachr. 329, 750–761.CrossRefGoogle Scholar
Riols, A., Rincon, F., Cossu, C., Lesur, G., Longaretti, P.-Y., Ogilvie, G.I. & Herault, J. 2013 Global bifurcations to subcritical magnetorotational dynamo action in Keplerian shear flow. J. Fluid Mech. 731, 1–45.Google Scholar
Riols, A., Rincon, F., Cossu, C., Lesur, G., Ogilvie, G. I. & Longaretti, P. 2015 Dissipative effects on the sustainment of a magnetorotational dynamo in Keplerian shear flow. Astron. Astrophys. 575, A14, 1–7.CrossRefGoogle Scholar
Schmid, P. J. & Henningson, D. S. 2001 Stability and Transition in Shear Flows. Springer.Google Scholar
Schneider, T. M., Eckhardt, B. & Vollmer, J. 2007 Statistical analysis of coherent structures in transitional pipe flow. Phys. Rev. E 75, 066313.Google Scholar
Schneider, T. M., Gibson, J. F., Lagha, M., De Lillo, F. & Eckhardt, B. 2008 Laminar-turbulent boundary in plane Couette flow. Phys. Rev. E 78, 37301.Google Scholar
Schoppa, W. & Hussain, F. 2002 Coherent structure generation in near-wall turbulence. J. Fluid Mech. 453, 57–108.Google Scholar
Smagorinsky, J. 1963 General circulation experiments with the primitive equations. Part I: the basic equations. Mon. Weath. Rev. 91, 99–164.Google Scholar
Smith, J. R. & Metzler, S. P. 1983 The characteristics of low-speed streaks in the near-wall region of a turbulent boundary layer. J. Fluid Mech. 129, 27–54.Google Scholar
Smits, A. J., McKeon, B. J. & Marusic, I. 2011 High-reynolds number wall turbulence. Annu. Rev. Fluid Mech. 43, 353–375.Google Scholar
Tillmark, N. & Alfredsson, H. 1994 Structures in turbulent plane Couette flow obtained from correlation measurements. In Advances in Turbulences V (ed. Benzi, R.), pp. 502–507. Kluwer.Google Scholar
Toh, S. & Itano, T. 2003 A periodic-like solution in channel flow. J. Fluid Mech. 481, 67–76.Google Scholar
Toh, S. & Itano, T. 2005 Interaction between a large-scale structure and near-wall structures in channel flow. J. Fluid Mech. 524, 249–262.CrossRefGoogle Scholar
Tomkins, C. D. & Adrian, R. J. 2003 Spanwise structure and scale growth in turbulent boundary layers. J. Fluid Mech. 490, 37–74.CrossRefGoogle Scholar
Tomkins, C. D. & Adrian, R. J. 2005 Energetic spanwise modes in the logarithmic layer of a turbulent boundary layer. J. Fluid Mech. 545, 141–162.Google Scholar
Tsukahara, T., Iwamoto, K. & Kawamura, H. 2007 POD analysis of large-scale structures through DNS of turbulence Couette flow. In Advances in Turbulence XI, pp. 245–247. Springer.Google Scholar
Tsukahara, T., Kawamura, H. & Shingai, K. 2006 DNS of turbulent Couette flow with emphasis on the large-scale structure in the core region. J. Turbul. 7, N19 (16 pp.).Google Scholar
Viswanath, D. 2008 The dynamics of transition to turbulence in plane Couette flow. In Mathematics and Computation: A Contemporary View. The Abel Symosium 2006. Springer.Google Scholar
Waleffe, F. 1995 Hydrodynamic stability and turbulence: beyond transients to a self-sustaining process. Stud. Appl. Maths 95, 319–343.CrossRefGoogle Scholar
Waleffe, F. 1998 Three-dimensional coherent states in plane shear flows. Phys. Rev. Lett. 81, 4140–4143.Google Scholar
Waleffe, F. 2003 Homotopy of exact coherent structures in plane shear flows. Phys. Fluids 15, 1517–1534.Google Scholar
Willis, A. P., Hwang, Y. & Cossu, C. 2010 Optimally amplified large-scale streaks and drag reduction in the turbulent pipe flow. Phys. Rev. E 82, 036321.Google Scholar
Zhou, J., Adrian, R. J., Balachandar, S. & Kendall, T. M. 1999 Mechanisms for generating coherent packets of hairpin vortices in channel flow. J. Fluid Mech. 387, 353–396.Google Scholar