Hostname: page-component-78c5997874-s2hrs Total loading time: 0 Render date: 2024-11-18T02:50:51.206Z Has data issue: false hasContentIssue false
  • English
  • Français

Particle capture and low-Reynolds-number flow around a circular cylinder

Published online by Cambridge University Press:  07 September 2012

Alexis Espinosa-Gayosso ,
Marco Ghisalberti ,
Gregory N. Ivey  and
Nicole L. Jones
Alexis Espinosa-Gayosso*
Affiliation:
School of Environmental Systems Engineering, University of Western Australia, Crawley, WA 6009, Australia UWA Oceans Institute, University of Western Australia, Crawley, WA 6009, Australia
Marco Ghisalberti
Affiliation:
School of Environmental Systems Engineering, University of Western Australia, Crawley, WA 6009, Australia
Gregory N. Ivey
Affiliation:
School of Environmental Systems Engineering, University of Western Australia, Crawley, WA 6009, Australia UWA Oceans Institute, University of Western Australia, Crawley, WA 6009, Australia
Nicole L. Jones
Affiliation:
School of Environmental Systems Engineering, University of Western Australia, Crawley, WA 6009, Australia UWA Oceans Institute, University of Western Australia, Crawley, WA 6009, Australia
*
†Email address for correspondence: Alexis.Espinosa.Gayosso@gmail.com
Get access Rights & Permissions [Opens in a new window]

Abstract

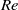Particle capture, whereby suspended particles contact and adhere to a solid surface (a ‘collector’), is an important mechanism in a range of environmental processes. In aquatic systems, typically characterized by low collector Reynolds numbers (), the rate of particle capture determines the efficiencies of a range of processes such as seagrass pollination, suspension feeding by corals and larval settlement. In this paper, we use direct numerical simulation (DNS) of a two-dimensional laminar flow to accurately quantify the rate of capture of low-inertia particles by a cylindrical collector for 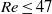(i.e. a range where there is no vortex shedding). We investigate the dependence of both the capture rate and maximum capture angle on both the collector Reynolds number and the ratio of particle size to collector size. The inner asymptotic expansion of Skinner (Q. J. Mech. Appl. Maths, vol. 28, 1975, pp. 333–340) for flow around a cylinder is extended and shown to provide an excellent framework for the prediction of particle capture and flow close to the leading face of a cylinder up to 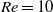. Our results fill a gap between theory and experiment by providing, for the first time, predictive capability for particle capture by aquatic collectors in a wide (and relevant) Reynolds number and particle size range.

JFM classification

Low-Reynolds-number flows: Low-Reynolds-number flows Multiphase and Particle-laden Flows: Particle/fluid flow Complex Fluids: Suspensions
Type
Papers
Information
Journal of Fluid Mechanics , Volume 710 , 10 November 2012 , pp. 362 - 378
Copyright
Copyright © Cambridge University Press 2012

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1. Ackerman, J. D. 1997 Submarine pollination in the marine angiosperm Zostera marina (Zosteraceae). II. Pollen transport in flow fields and capture by stigmas. Am. J. Bot. 84 (8), 1110–1119.Google Scholar
2. Ackerman, J. D. 2006 Sexual reproduction of seagrasses: pollination in the marine context. In Seagrasses: Biology, Ecology and Conservation (ed. Larkum, A. W. D., Orth, R. J. & Duarte, C. M. ). Springer.Google Scholar
3. Davies, C. N. 1950 Viscous flow transverse to a circular cylinder. Proc. Phys. Soc. Lond. B 63 (364), 288–296.Google Scholar
4. Davies, C. N. & Peetz, C. V. 1956 Impingement of particles on a transverse cylinder. Proc. R. Soc. Lond. A 234 (1197), 268–295.Google Scholar
5. Ferziger, J. H. & Perić, M. 2002 Computational Methods for Fluid Dynamics, 3rd edn. Springer.CrossRefGoogle Scholar
6. Friedlander, S. K. 1967 Particle diffusion in low-speed flows. J. Colloid Interface Sci. 23 (2), 157–164.Google Scholar
7. Friedlander, S. K. 2000 Smoke, Dust and Haze. Fundamentals of Aerosol Dynamics, 2nd edn. Oxford University Press.Google Scholar
8. Fuchs, N. A. 1964 The Mechanics of Aerosols, 1st edn. Pergamon.Google Scholar
9. Harvey, M., Bourget, E. & Ingram, R. G. 1995 Experimental-evidence of passive accumulation of marine bivalve larvae on filamentous epibenthic structures. Limnol. Oceanogr. 40 (1), 94–104.Google Scholar
10. Haugen, N. E. L. & Kragset, S. 2010 Particle impaction on a cylinder in a crossflow as function of Stokes and Reynolds numbers. J. Fluid Mech. 661, 239–261.Google Scholar
11. Humphries, S. 2009 Filter feeders and plankton increase particle encounter rates through flow regime control. Proc. Natl Acad. Sci. USA 106 (19), 7882–7887.Google Scholar
12. Huner, B. & Hussey, R. G. 1977 Cylinder drag at low Reynolds number. Phys. Fluids 20 (8), 1211–1218.CrossRefGoogle Scholar
13. Kaplun, S. 1957 Low Reynolds number flow past a circular cylinder. J. Math. Mech. 6 (4), 595–603.Google Scholar
14. Keller, J. B. & Ward, M. J. 1996 Asymptotics beyond all orders for a low Reynolds number flow. J. Engng Maths 30 (1–2), 253–265.Google Scholar
15. Lamb, H. 1911 On the uniform motion of a sphere through a viscous fluid. Phil. Mag. Series 6 21 (121), 112–121.Google Scholar
16. Lange, C. F., Durst, F. & Breuer, M. 1998 Momentum and heat transfer from cylinders in laminar crossflow at . Intl J. Heat Mass Transfer 41 (22), 3409–3430.Google Scholar
17. Lee, K. W. & Gieseke, J. A. 1980 Note on the approximation of interceptional collection efficiencies. J. Aerosol Sci. 11 (4), 335–341.CrossRefGoogle Scholar
18.OpenFOAM. 2012 http://www.openfoam.com/.Google Scholar
19. Oseen, C. W. 1910 Über die Stokes’sche Formel, und über eine verwandte Aufgabe in der Hydrodynamik. Ark. Mat. Astron. Fys. 6 (29), 1–20.Google Scholar
20. Palmer, M. R., Nepf, H. M., Petterson, T. J. R. & Ackerman, J. D. 2004 Observations of particle capture on a cylindrical collector: implications for particle accumulation and removal in aquatic systems. Limnol. Oceanogr. 49 (1), 76–85.CrossRefGoogle Scholar
21. Patankar, S. V. 1980 Numerical Heat Transfer and Fluid Flow, 1st edn. Taylor and Francis.Google Scholar
22. Phillips, C. G. & Kaye, S. R. 1999 The influence of the viscous boundary layer on the critical Stokes number for particle impaction near a stagnation point. J. Aerosol Sci. 30 (6), 709–718.Google Scholar
23. Posdziech, O. & Grundmann, R. 2007 A systematic approach to the numerical calculation of fundamental quantities of the two-dimensional flow over a circular cylinder. J. Fluids Struct. 23 (3), 479–499.CrossRefGoogle Scholar
24. Proudman, I. & Pearson, J. R. A. 1957 Expansions at small Reynolds numbers for the flow past a sphere and a circular cylinder. J. Fluid Mech. 2 (3), 237–262.CrossRefGoogle Scholar
25. Rubenstein, D. I. & Koehl, M. A. R. 1977 Mechanisms of filter feeding: some theoretical considerations. Am. Nat. 111 (981), 981–994.Google Scholar
26. Sen, S., Mittal, S. & Biswas, G. 2009 Steady separated flow past a circular cylinder at low Reynolds numbers. J. Fluid Mech. 620, 89–119.Google Scholar
27. Shimeta, J. 1993 Diffusional encounter of submicrometre particles and small-cells by suspension feeders. Limnol. Oceanogr. 38 (2), 456–465.Google Scholar
28. Shimeta, J. & Jumars, P. A. 1991 Physical mechanisms and rates of particle capture by suspension-feeders. Oceanogr. Mar. Biol. 29, 191–257.Google Scholar
29. Shimeta, J. & Koehl, M. A. R. 1997 Mechanisms of particle selection by tentaculate suspension feeders during encounter, retention, and handling. J. Expl Mar. Biol. Ecol. 209 (1–2), 47–73.Google Scholar
30. Skinner, L. A. 1975 Generalized expansions for slow flow past a cylinder. Q. J. Mech. Appl. Maths 28 (3), 333–340.Google Scholar
31. Stokes, G. G. 1851 On the effect of the internal friction of fluids on the motion of pendulums. Trans. Camb. Phil. Soc. 9 (Part II), 8–106.Google Scholar
32. Tritton, D. J. 1959 Experiments on the flow past a circular cylinder at low Reynolds numbers. J. Fluid Mech. 6 (4), 547–567.Google Scholar
33. Veysey, J. & Goldenfeld, N. 2007 Simple viscous flows: from boundary layers to the renormalization group. Rev. Mod. Phys. 79 (3), 883–927.CrossRefGoogle Scholar
34. Wildish, D. & Kristmanson, D. 1997 Benthic Suspension Feeders and Flow, 1st edn. Cambridge University Press.Google Scholar
35. Wu, M. H., Wen, C. Y., Yen, R. H., Weng, M. C. & Wang, A. B. 2004 Experimental and numerical study of the separation angle for flow around a circular cylinder at low Reynolds number. J. Fluid Mech. 515, 233–260.CrossRefGoogle Scholar