Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-25T13:57:25.487Z Has data issue: false hasContentIssue false
  • English
  • Français

Patterns of a creeping water-spout flow

Published online by Cambridge University Press:  10 March 2014

Miguel Herrada  and
Vladimir Shtern
Miguel Herrada*
Affiliation:
E. S. I., Universidad de Sevilla, Camino de los Descubrimientos s/n 41092, Spain
Vladimir Shtern
Affiliation:
Shtern Research and Consulting, Houston, TX 77096, USA
*
†Email address for correspondence: herrada@us.es
Get access Rights & Permissions [Opens in a new window]

Abstract

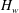This paper explains a mechanism of eddy formation in a slow air–water motion, driven by the rotating top disk, in a vertical sealed cylinder. The numerical simulations reveal nine changes in the flow topology as water volume fraction $H_{w}$ varies from 0 to 1. At 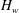$H_{w}$ around 0.8, there are two large regions of the clockwise meridional circulation, one in air and one in water. These regions are separated by two small cells of the anticlockwise circulation adjacent to the interface near the sidewall in water and near the axis in air. The air cell is a thin layer and topologically is a bubble–ring for 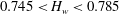$0.745 < H_{w} < 0.785$. Alterations of this flow pattern are explored as (i) pressure increases, (ii) the bottom disk co-rotates and (iii) the top-disk rotation speeds up. This paper provides the physical reasoning behind the flow transformations; the results are of fundamental interest and can be utilized in bioreactors.

JFM classification

Multiphase and Particle-laden Flows: Multiphase flow Vortex Flows: Vortex dynamics Vortex Flows: Vortex Flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 744 , 10 April 2014 , pp. 65 - 88
Copyright
© 2014 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Batchelor, G. K. 1967 An Introduction to Fluid Dynamics. Cambridge University Press.Google Scholar
Blake, J. 1979 On the generation of viscous toroidal eddies in a cylinder. J. Fluid Mech. 95, 209–222.CrossRefGoogle Scholar
Brady, P. T., Herman, M. & Lopez, J. M. 2012a Two-fluid confined flow in a cylinder driven by a rotating end wall. Phys. Rev. E 85, 016306.Google Scholar
Brady, P. T., Herman, M. & Lopez, J. M. 2012b Addendum to ‘Two-fluid confined flow in a cylinder driven by a rotating end wall’. Phys. Rev. E 85, 067301.Google Scholar
Brøns, M. 1994 Topological fluid dynamics of interfacial flows. Phys. Fluids 6, 2730–2737.Google Scholar
Brøns, M. 2007 Streamline topology: patterns in fluid flows and their bifurcations. Adv. Appl. Mech. 41, 1–42.Google Scholar
Brøns, M., Voigt, L. K. & Sørensen, J. N. 2001 Topology of vortex breakdown bubbles in a cylinder with a rotating bottom and a free surface. J. Fluid Mech. 428, 133–148.Google Scholar
Gelfgat, A. Yu., Bar-Yoseph, P. Z. & Solan, A. 2001 Three-dimensional instability of axisymmetric flow in a rotating lid cylinder enclosure. J. Fluid Mech. 438, 363–377.Google Scholar
Gürcan, F., Gaskell, P. H., Savage, M. D. & Wilson, M. C. T. 2003 Eddy genesis and transformations of Stokes flow in a double-lid driven cavity. Proc. Inst. Mech. Engrs C 217, 353–364.Google Scholar
Hall, O., Hills, C. P. & Gilbert, A. D. 2007 Slow flow between concentric cones. Q. J. Mech. Appl. Maths. 60, 27–48.CrossRefGoogle Scholar
Happel, J. R. & Brenner, H. 1965 Low Reynolds number hydrodynamics. Springer.Google Scholar
Herrada, M. A., Shtern, V. N. & López-Herrera, J. M. 2013a Off-axis vortex breakdown in a shallow whirlpool. Phys. Rev. E 87, 063016.CrossRefGoogle Scholar
Herrada, M. A., Shtern, V. N. & López-Herrera, J. M. 2013b Vortex breakdown in a water-spout flow. Phys. Fluids 25, 093604.Google Scholar
Herrada, M. A., Shtern, V. N. & López-Herrera, J. M.2013c Bubble-ring cells in a whirlpool flow. Manuscript submitted in Phys. Rev. E.Google Scholar
Hills, C. P. 2001 Eddies induced in cylindrical containers by a rotating end wall. Phys. Fluids 13, 2279–2286.Google Scholar
Liow, K. Y. S., Tan, B. T., Thouas, G. & Thompson, M. C. 2009 CFD modeling of the steady-state momentum and oxygen transport in a bioreactor that is driven by a rotating disk. Mod. Phys. Lett. B 23 (2), 121–127.CrossRefGoogle Scholar
Lo Jacono, D., Nazarinia, M. & Brøns, M. 2009 Experimental vortex breakdown topology in a cylinder with a free surface. Phys. Fluids 21, 111704.CrossRefGoogle Scholar
Moffatt, H. K. 1964 Viscous and resistive eddies near a sharp corner. J. Fluid Mech. 18, 1–18.Google Scholar
Ramazanov, Yu. A., Kislykh, V.I., Kosyuk, I. P., Bakuleva, N. V. & Shchurikhina, V. V. 2007 Industrial production of vaccines using embryonic cells in gas-vortex gradient-less bioreactors. In New Aspects of Biotechnology and Medicine (ed. Egorov, A. M.), pp. 87–91.Google Scholar
Shankar, P. N. & Deshpande, M. D. 2000 Fluid mechanics in the driven cavity. Annu. Rev. Fluid Mech. 32, 93–136.Google Scholar
Shtern, V. 2012a A flow in the depth of infinite annular cylindrical cavity. J. Fluid Mech. 711, 667–680.CrossRefGoogle Scholar
Shtern, V. 2012b Counterflows. Cambridge University Press.Google Scholar
Wakiya, S. 1976 Axisymmetric flow of a viscous fluid near the vertex of a body. J. Fluid Mech. 78, 737–747.Google Scholar
Wilson, M. C. T., Gaskell, P. H. & Savage, M. D. 2005 Nested separatrices in simple shear flows: the effect of localized disturbances on stagnation lines. Phys. Fluids 17, 093601.Google Scholar