Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-20T12:48:29.678Z Has data issue: false hasContentIssue false
  • English
  • Français

Phase-based control of periodic flows

Published online by Cambridge University Press:  29 September 2021

Aditya G. Nair Open the ORCID record for Aditya G. Nair [Opens in a new window] ,
Kunihiko Taira Open the ORCID record for Kunihiko Taira [Opens in a new window] ,
Bingni W. Brunton Open the ORCID record for Bingni W. Brunton [Opens in a new window]  and
Steven L. Brunton Open the ORCID record for Steven L. Brunton [Opens in a new window]
Aditya G. Nair*
Affiliation:
Department of Mechanical Engineering, University of Nevada, Reno, NV 89557, USA
Kunihiko Taira
Affiliation:
Department of Mechanical and Aerospace Engineering, University of California, Los Angeles, CA 90095, USA
Bingni W. Brunton
Affiliation:
Department of Biology, University of Washington, Seattle, WA 98195, USA
Steven L. Brunton
Affiliation:
Department of Mechanical Engineering, University of Washington, Seattle, WA 98195, USA
*
†Email address for correspondence: adityan@unr.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

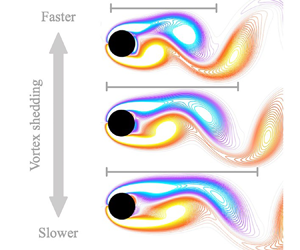
Unsteady bluff-body flows exhibit dominant oscillatory behaviour owing to periodic vortex shedding. The ability to manipulate this vortex shedding is critical to improving the aerodynamic performance of bodies in a flow. This goal requires a precise understanding of how the perturbations affect the asymptotic behaviour of the oscillatory flow and of the ability to control transient dynamics. In this work, we develop an energy-efficient flow-control strategy to alter the oscillation phase of time-periodic fluid flows rapidly. First, we perform a phase-sensitivity analysis to construct a reduced-order model for the response of the flow oscillation to impulsive control inputs at various phases. Next, we introduce a real-time optimal phase-control strategy based on the phase-sensitivity function obtained by solving the associated Euler–Lagrange equations as a two-point boundary-value problem. Our approach is demonstrated for the incompressible laminar flow past a circular cylinder and an airfoil. We show the effectiveness of phase control with different actuation inputs, including blowing and rotary control. Moreover, our control approach is a sensor-based approach without the need for access to high-dimensional measurements of the entire flow field.

JFM classification

Vortex Flows: Vortex shedding Mathematical Foundations: Variational methods
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 927 , 25 November 2021 , A30
Check for updates
Copyright
© The Author(s), 2021. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Amitay, M. & Glezer, A. 2002 Controlled transients of flow reattachment over stalled airfoils. Intl J. Heat Fluid Flow 23 (5), 690–699.CrossRefGoogle Scholar
Amitay, M. & Glezer, A. 2006 Flow transients induced on a 2D airfoil by pulse-modulated actuation. Exp. Fluids 40 (2), 329–331.CrossRefGoogle Scholar
Bagheri, S. 2013 Koopman-mode decomposition of the cylinder wake. J. Fluid Mech. 726, 596–623.CrossRefGoogle Scholar
Barkley, D. & Henderson, R.D. 1996 Three-dimensional Floquet stability analysis of the wake of a circular cylinder. J. Fluid Mech. 322, 215–241.CrossRefGoogle Scholar
Bewley, T.R. 2001 Flow control: new challenges for a new renaissance. Prog. Aerosp. Sci. 37 (1), 21–58.CrossRefGoogle Scholar
Bhattacharjee, D., Hemati, M., Klose, B. & Jacobs, G. 2018 Optimal actuator selection for airfoil separation control. In 2018 Flow Control Conference, p. 3692.Google Scholar
Brown, E., Moehlis, J. & Holmes, P. 2004 On the phase reduction and response dynamics of neural oscillator populations. Neural Comput. 16 (4), 673–715.CrossRefGoogle ScholarPubMed
Brunton, S.L. & Noack, B.R. 2015 Closed-loop turbulence control: progress and challenges. Appl. Mech. Rev. 67, 050801.CrossRefGoogle Scholar
Brunton, S.L., Noack, B.R. & Koumoutsakos, P. 2020 Machine learning for fluid mechanics. Annu. Rev. Fluid Mech. 52, 477–508.CrossRefGoogle Scholar
Brunton, S.L., Proctor, J.L. & Kutz, J.N. 2016 Discovering governing equations from data by sparse identification of nonlinear dynamical systems. Proc. Natl Acad. Sci. USA 113 (15), 3932–3937.CrossRefGoogle ScholarPubMed
Colonius, T. & Taira, K. 2008 A fast immersed boundary method using a nullspace approach and multi-domain far-field boundary conditions. Comput. Meth. Appl. Mech. Engng 197, 2131–2146.CrossRefGoogle Scholar
Colonius, T. & Williams, D.R. 2011 Control of vortex shedding on two-and three-dimensional aerofoils. Phil. Trans. R. Soc. Lond. A 369 (1940), 1525–1539.Google ScholarPubMed
Darabi, A. & Wygnanski, I. 2004 Active management of naturally separated flow over a solid surface. Part 2. The separation process. J. Fluid Mech. 510, 131–144.CrossRefGoogle Scholar
Dickinson, M.H., Farley, C.T., Full, R.J., Koehl, M.A.R., Kram, R. & Lehman, S. 2000 How animals move: an integrative view. Science 288 (5463), 100–106.CrossRefGoogle Scholar
Dickinson, M.H., Lehmann, F. & Sane, S.P. 1999 Wing rotation and the aerodynamic basis of insect flight. Science 284 (5422), 1954–1960.CrossRefGoogle ScholarPubMed
Eldredge, J.D. & Jones, A.R. 2019 Leading-edge vortices: mechanics and modeling. Annu. Rev. Fluid Mech. 51, 75–104.CrossRefGoogle Scholar
Garcia, C.E., Prett, D.M. & Morari, M. 1989 Model predictive control: theory and practice – a survey. Automatica 25 (3), 335–348.CrossRefGoogle Scholar
Gerhard, J., Pastoor, M., King, R., Noack, B., Dillmann, A., Morzynski, M. & Tadmor, G. 2003 Model-based control of vortex shedding using low-dimensional Galerkin models. AIAA Paper 2003-4262.CrossRefGoogle Scholar
Giannetti, F., Camarri, S. & Citro, V. 2019 Sensitivity analysis and passive control of the secondary instability in the wake of a cylinder. J. Fluid Mech. 864, 45–72.CrossRefGoogle Scholar
Guckenheimer, J. 1975 Isochrons and phaseless sets. J. Math. Biol. 1 (3), 259–273.CrossRefGoogle ScholarPubMed
Herbert, T., Bertolotti, F.P. & Santos, G.R. 1987 Floquet analysis of secondary instability in shear flows. In Stability of Time Dependent and Spatially Varying Flows, pp. 43–57. Springer.CrossRefGoogle Scholar
Hornik, K., Stinchcombe, M. & White, H. 1989 Multilayer feedforward networks are universal approximators. Neural Networks 2 (5), 359–366.CrossRefGoogle Scholar
Joe, W.T., Colonius, T. & MacMynowski, D.G. 2011 Feedback control of vortex shedding from an inclined flat plate. Theor. Comput. Fluid Dyn. 25 (1–4), 221–232.CrossRefGoogle Scholar
Kaiser, E., Kutz, J.N. & Brunton, S.L. 2018 Sparse identification of nonlinear dynamics for model predictive control in the low-data limit. Proc. R. Soc. Lond. A 474 (2219), 20180335.Google ScholarPubMed
Kaiser, E., Noack, B.R., Cordier, L., Spohn, A., Segond, M., Abel, M., Daviller, G. & Niven, R.K. 2014 Cluster-based reduced-order modelling of a mixing layer. J. Fluid Mech. 754, 365–414.CrossRefGoogle Scholar
Kajishima, T. & Taira, K. 2017 Computational Fluid Dynamics: Incompressible Turbulent Flows. Springer.CrossRefGoogle Scholar
Kasdin, N.J. 1995 Runge–Kutta algorithm for the numerical integration of stochastic differential equations. J. Guid. Control Dyn. 18 (1), 114–120.CrossRefGoogle Scholar
Kawamura, Y. & Nakao, H. 2013 Collective phase description of oscillatory convection. Chaos 23 (4), 043129.CrossRefGoogle ScholarPubMed
Kawamura, Y. & Nakao, H. 2015 Phase description of oscillatory convection with a spatially translational mode. Physica D 295, 11–29.CrossRefGoogle Scholar
Khodkar, M.A., Klamo, J.T. & Taira, K. 2021 Phase-locking of laminar wake to periodic vibrations of a circular cylinder. Phys. Rev. Fluids 6 (3), 034401.CrossRefGoogle Scholar
Khodkar, M.A. & Taira, K. 2020 Phase-synchronization properties of laminar cylinder wake for periodic external forcings. J. Fluid Mech. 904.CrossRefGoogle Scholar
Kim, J. & Bewley, T.R. 2007 A linear systems approach to flow control. Annu. Rev. Fluid Mech. 39, 383–417.CrossRefGoogle Scholar
Kuramoto, Y. 1984 Chemical Oscillations, Waves, and Turbulence. Springer.CrossRefGoogle Scholar
Kuramoto, Y. & Nakao, H. 2019 On the concept of dynamical reduction: the case of coupled oscillators. Phil. Trans. R. Soc. Lond. A 377 (2160), 20190041.Google ScholarPubMed
Malkin, I.G. 1949 The Methods of Lyapunov and Poincare in the Theory of Nonlinear Oscillations. Gostexizdat.Google Scholar
Mauroy, A. & Mezić, I. 2012 On the use of Fourier averages to compute the global isochrons of (quasi) periodic dynamics. Chaos 22 (3), 033112.CrossRefGoogle ScholarPubMed
Mauroy, A. & Mezić, I. 2018 Global computation of phase-amplitude reduction for limit-cycle dynamics. Chaos 28 (7), 073108.CrossRefGoogle ScholarPubMed
Mauroy, A., Mezić, I. & Moehlis, J. 2013 Isostables, isochrons, and Koopman spectrum for the action–angle representation of stable fixed point dynamics. Physica D 261, 19–30.CrossRefGoogle Scholar
Mezić, I. 2005 Spectral properties of dynamical systems, model reduction and decompositions. Nonlinear Dyn. 41 (1–3), 309–325.CrossRefGoogle Scholar
Moehlis, J. 2014 Improving the precision of noisy oscillators. Physica D 272, 8–17.CrossRefGoogle Scholar
Moehlis, J., Shea-Brown, E. & Rabitz, H. 2006 Optimal inputs for phase models of spiking neurons. J. Comput. Nonlinear Dyn. 1 (4), 358–367.CrossRefGoogle Scholar
Monga, B., Wilson, D., Matchen, T. & Moehlis, J. 2019 Phase reduction and phase-based optimal control for biological systems: a tutorial. Biol. Cybern. 113 (1–2), 11–46.CrossRefGoogle ScholarPubMed
Morari, M. & Lee, J.H. 1999 Model predictive control: past, present and future. Comput. Chem. Engng 23 (4–5), 667–682.CrossRefGoogle Scholar
Munday, P.M. & Taira, K. 2013 On the lock-on of vortex shedding to oscillatory actuation around a circular cylinder. Phys. Fluids 25, 013601.CrossRefGoogle Scholar
Nair, A.G., Yeh, C.A., Kaiser, E., Noack, B.R., Brunton, S.L. & Taira, K. 2019 Cluster-based feedback control of turbulent post-stall separated flows. J. Fluid Mech. 875, 345–375.CrossRefGoogle Scholar
Nakao, H. 2016 Phase reduction approach to synchronisation of nonlinear oscillators. Contemp. Phys. 57 (2), 188–214.CrossRefGoogle Scholar
Pastoor, M., Henning, L., Noack, B.R., King, R. & Tadmor, G. 2008 Feedback shear layer control for bluff body drag reduction. J. Fluid Mech. 608, 161–196.CrossRefGoogle Scholar
Ramananarivo, S., Godoy-Diana, R. & Thiria, B. 2011 Rather than resonance, flapping wing flyers may play on aerodynamics to improve performance. Proc. Natl Acad. Sci. USA 108 (15), 5964–5969.CrossRefGoogle ScholarPubMed
Roma, A.M., Peskin, C.S. & Berger, M.J. 1999 An adaptive version of the immersed boundary method. J. Comput. Phys. 153, 509–534.CrossRefGoogle Scholar
Schmid, P.J. 2010 Dynamic mode decomposition of numerical and experimental data. J. Fluid Mech. 656, 5–28.CrossRefGoogle Scholar
Shyy, W., Kang, C., Chirarattananon, P., Ravi, S. & Liu, H. 2016 Aerodynamics, sensing and control of insect-scale flapping-wing flight. Proc. R. Soc. Lond. A 472 (2186), 20150712.Google ScholarPubMed
Shyy, W., Lian, Y., Tang, J., Viieru, D. & Liu, H. 2008 Aerodynamics of Low Reynolds Number Flyers. Cambridge University Press.CrossRefGoogle Scholar
Siegel, S., Cohen, K. & McLaughlin, T. 2003 Feedback control of a circular cylinder wake in experiment and simulation. AIAA Paper 2003-3569.CrossRefGoogle Scholar
Sipp, D. & Lebedev, A. 2007 Global stability of base and mean flows: a general approach and its applications to cylinder and open cavity flows. J. Fluid Mech. 593, 333–358.CrossRefGoogle Scholar
Sponberg, S & Daniel, T.L. 2012 Abdicating power for control: a precision timing strategy to modulate function of flight power muscles. Proc. R. Soc. Lond. B 279 (1744), 3958–3966.Google ScholarPubMed
Stuart, J.T. 1960 On the non-linear mechanics of wave disturbances in stable and unstable parallel flows. Part 1. The basic behaviour in plane Poiseuille flow. J. Fluid Mech. 9 (3), 353–370.CrossRefGoogle Scholar
Taira, K. & Nakao, H. 2018 Phase-response analysis of synchronization for periodic flows. J. Fluid Mech. 846.CrossRefGoogle Scholar
Takata, S., Kato, Y. & Nakao, H. 2021 Fast optimal entrainment of limit-cycle oscillators by strong periodic inputs via phase-amplitude reduction and Floquet theory. arXiv:2104.09944.CrossRefGoogle Scholar
Wang, C. & Eldredge, J. 2013 Low-order phenomenological modeling of leading-edge vortex formation. Theor. Comput. Fluid Dyn. 27 (5), 577–598.CrossRefGoogle Scholar
Williams, D.R., Tadmor, G., Colonius, T., Kerstens, W., Quach, V. & Buntain, S. 2009 Lift response of a stalled wing to pulsatile disturbances. AIAA J. 47 (12), 3031–3037.CrossRefGoogle Scholar
Wilson, D. 2020 Stabilization of weakly unstable fixed points as a common dynamical mechanism of high-frequency electrical stimulation. Sci. Rep. 10 (1), 1–21.CrossRefGoogle ScholarPubMed
Wilson, D. & Moehlis, J. 2016 Isostable reduction of periodic orbits. Phys. Rev. E 94 (5), 052213.CrossRefGoogle ScholarPubMed
Winfree, A.T. 2001 The Geometry of Biological Time. Springer.CrossRefGoogle Scholar
Wu, T.Y. 2011 Fish swimming and bird/insect flight. Annu. Rev. Fluid Mech. 43, 25–58.CrossRefGoogle Scholar