Hostname: page-component-8678677fb7-bvjg6 Total loading time: 0 Render date: 2026-09-17T02:36:19.976Z Has data issue: false hasContentIssue false
  • English
  • Français

Rotation of a low-Reynolds-number watermill: theory and simulations

Published online by Cambridge University Press:  15 June 2018

Lailai Zhu Open the ORCID record for Lailai Zhu [Opens in a new window]  and
Howard A. Stone
Lailai Zhu
Affiliation:
Department of Mechanical and Aerospace Engineering, Princeton University, Princeton, NJ 08544, USA Linné Flow Centre and Swedish e-Science Research Centre (SeRC), KTH Mechanics, Stockholm, SE-10044, Sweden
Howard A. Stone*
Affiliation:
Department of Mechanical and Aerospace Engineering, Princeton University, Princeton, NJ 08544, USA
*
†Email address for correspondence: hastone@princeton.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

Recent experiments have demonstrated that small-scale rotary devices installed in a microfluidic channel can be driven passively by the underlying flow alone without resorting to conventionally applied magnetic or electric fields. In this work, we conduct a theoretical and numerical study on such a flow-driven ‘watermill’ at low Reynolds number, focusing on its hydrodynamic features. We model the watermill by a collection of equally spaced rigid rods. Based on the classical resistive force (RF) theory and direct numerical simulations, we compute the watermill’s instantaneous rotational velocity as a function of its rod number 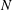$N$, position and orientation. When $N\geqslant 4$, the RF theory predicts that the watermill’s rotational velocity is independent of $N$ and its orientation, implying the full rotational symmetry (of infinite order), even though the geometrical configuration exhibits a lower-fold rotational symmetry; the numerical solutions including hydrodynamic interactions show a weak dependence on $N$ and the orientation. In addition, we adopt a dynamical system approach to identify the equilibrium positions of the watermill and analyse their stability. We further compare the theoretically and numerically derived rotational velocities, which agree with each other in general, while considerable discrepancy arises in certain configurations owing to the hydrodynamic interactions neglected by the RF theory. We confirm this conclusion by employing the RF-based asymptotic framework incorporating hydrodynamic interactions for a simpler watermill consisting of two or three rods and we show that accounting for hydrodynamic interactions can significantly enhance the accuracy of the theoretical predictions.

JFM classification

Low-Reynolds-number flows: Low-Reynolds-number flows Micro-/Nano-fluid dynamics: MEMS/NEMS Micro-/Nano-fluid dynamics: Microfluidics

Information

Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 849 , 25 August 2018 , pp. 57 - 75
Check for updates
Copyright
© 2018 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Agarwal, A. K., Sridharamurthy, S. S., Beebe, D. J. & Jiang, H. 2005 Programmable autonomous micromixers and micropumps. J. Microelectromech. Syst. 14 (6), 1409–1421.Google Scholar
Ahn, C. H. & Allen, M. G. 1995 Fluid micropumps based on rotary magnetic actuators. In Micro Electro Mechanical Systems, 1995, MEMS’95, Proceedings, p. 408. IEEE.Google Scholar
Attia, R.2008 Modifications de surfaces et intégration de MEMS pour les laboratoires sur puce. PhD thesis, Université Pierre et Marie Curie-Paris VI.Google Scholar
Attia, R., Pregibon, D. C., Doyle, P. S., Viovy, J.-L. & Bartolo, D. 2009 Soft microflow sensors. Lab on a Chip 9 (9), 1213–1218.Google Scholar
Bart, S. F., Mehregany, M., Tavrow, L. S., Lang, J. H. & Senturia, S. D. 1992 Electric micromotor dynamics. IEEE Trans. Electron Dev. 39 (3), 566–575.Google Scholar
Barta, E. & Liron, N. 1988 Slender body interactions for low Reynolds numbers – Part I: body–wall interactions. SIAM J. Appl. Maths 48 (5), 992–1008.Google Scholar
van den Beld, W. T. E., Cadena, N. L., Bomer, J., de Weerd, E. L., Abelmann, L., van den Berg, A. & Eijkel, J. C. T. 2015 Bidirectional microfluidic pumping using an array of magnetic Janus microspheres rotating around magnetic disks. Lab on a Chip 15 (13), 2872–2878.Google Scholar
Day, R. F. & Stone, H. A. 2000 Lubrication analysis and boundary integral simulations of a viscous micropump. J. Fluid Mech. 416, 197–216.Google Scholar
Döpper, J., Clemens, M., Ehrfeld, W., Jung, S., Kaemper, K. P. & Lehr, H. 1997 Micro gear pumps for dosing of viscous fluids. J. Micromech. Microengng 7 (3), 230–232.Google Scholar
Jeffery, G. B. 1922 The motion of ellipsoidal particles immersed in a viscous fluid. Proc. R. Soc. Lond. A 102 (715), 161–179.Google Scholar
Johnson, R. E. & Brokaw, C. J. 1979 Flagellar hydrodynamics. A comparison between resistive-force theory and slender-body theory. Biophys. J. 25 (1), 113–127.Google Scholar
Katz, D. F. 1974 On the propulsion of micro-organisms near solid boundaries. J. Fluid Mech. 64 (1), 33–49.Google Scholar
Lighthill, M. J. 1975 Mathematical Biofluiddynamics. SIAM.Google Scholar
Man, Y., Koens, L. & Lauga, E. 2016 Hydrodynamic interactions between nearby slender filaments. Europhys. Lett. 116 (2), 24002.Google Scholar
Mestre, N. J. De 1973 Low-Reynolds-number fall of slender cylinders near boundaries. J. Fluid Mech. 58 (4), 641–656.Google Scholar
Moon, B. U., Tsai, S. S. H. & Hwang, D. K. 2015 Rotary polymer micromachines: in situ fabrication of microgear components in microchannels. Microfluid. Nanofluid. 19 (1), 67–74.Google Scholar
Nazockdast, E., Rahimian, A., Zorin, D. & Shelley, M. 2017 A fast platform for simulating semi-flexible fiber suspensions applied to cell mechanics. J. Comput. Phys. 329, 173–209.Google Scholar
Pak, O. S., Zhu, L., Brandt, L. & Lauga, E. 2012 Micropropulsion and microrheology in complex fluids via symmetry breaking. Phys. Fluids 24 (10), 103102.Google Scholar
Ross, R. F. & Klingenberg, D. J. 1997 Dynamic simulation of flexible fibers composed of linked rigid bodies. J. Chem. Phys. 106 (7), 2949–2960.Google Scholar
Russel, W. B., Hinch, E. J., Leal, L. G. & Tieffenbruck, G. 1977 Rods falling near a vertical wall. J. Fluid Mech. 83 (2), 273–287.Google Scholar
Ryu, K. S., Shaikh, K., Goluch, E., Fan, Z. & Liu, C. 2004 Micro magnetic stir-bar mixer integrated with parylene microfluidic channels. Lab on a Chip 4 (6), 608–613.Google Scholar
Saintillan, D. & Shelley, M. J. 2007 Orientational order and instabilities in suspensions of self-locomoting rods. Phys. Rev. Lett. 99 (5), 058102.Google Scholar
Sen, M., Wajerski, D. & Gad-el-Hak, M. 1996 A novel pump for MEMS applications. Trans. ASME J. Fluids Engng 118 (3), 624–627.Google Scholar
Strogatz, S. H. 2014 Nonlinear Dynamics and Chaos: with Applications to Physics, Biology, Chemistry, and Engineering. Westview Press.Google Scholar
Whitesides, G. M. 2006 The origins and the future of microfluidics. Nature 442 (7101), 368–373.Google Scholar
Yamamoto, S. & Matsuoka, T. 1995 Dynamic simulation of fiber suspensions in shear flow. J. Chem. Phys. 102 (5), 2254–2260.Google Scholar
Zaki, T. G., Sen, M. & Gad-el-Hak, M. 1994 Numerical and experimental investigation of flow past a freely rotatable square cylinder. J. Fluids Struct. 8 (7), 555–582.Google Scholar