Article contents
Rotational dynamics of a neutrally buoyant prolate spheroid in viscoelastic shear flows at finite Reynolds numbers
Published online by Cambridge University Press: 03 March 2023
Abstract
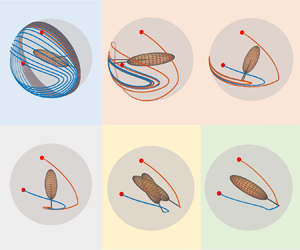
Non-spherical particles exhibit peculiar behaviour in non-Newtonian flows. In this paper, we numerically investigate the dynamics of a neutrally buoyant prolate spheroid immersed in viscoelastic shear flows at finite Reynolds numbers by means of the immersed boundary method. Our results show that the period of particle rotation changes monotonically with the solvent viscosity ratio but non-monotonically with the mobility factor. Furthermore, we find five rotation modes of the spheroid under the effects of fluid inertia and fluid rheology in the present flow configuration. With weak fluid inertia, the particle rotation rate is remarkably reduced by fluid elasticity, which also induces asymmetric rotational behaviour. While the particle tends to tumble in the shear plane with weak fluid elasticity and moderate fluid inertia. However, as the fluid elasticity increases, the particle rotates with a newly observed mode, named the asymmetric-kayaking mode, which is classified by two additional critical elastic numbers that differ from the earlier studies on Stokesian viscoelastic shear flows. The present findings imply the importance of fluid inertia and fluid elasticity on the particle dynamics and could be potentially used to control the particle orientations in viscoelastic fluid flows.
Information
- Type
- JFM Papers
- Information
- Copyright
- © The Author(s), 2023. Published by Cambridge University Press
References
REFERENCES
- 5
- Cited by


