Hostname: page-component-586b7cd67f-t7czq Total loading time: 0 Render date: 2024-11-26T03:17:26.173Z Has data issue: false hasContentIssue false
  • English
  • Français

Sensitivity and feedback of wind-farm-induced gravity waves

Published online by Cambridge University Press:  16 January 2019

Dries Allaerts Open the ORCID record for Dries Allaerts [Opens in a new window]  and
Johan Meyers Open the ORCID record for Johan Meyers [Opens in a new window]
Dries Allaerts*
Affiliation:
KU Leuven, Department of Mechanical Engineering, Celestijnenlaan 300 – bus 2421, B3001 Leuven, Belgium
Johan Meyers
Affiliation:
KU Leuven, Department of Mechanical Engineering, Celestijnenlaan 300 – bus 2421, B3001 Leuven, Belgium
*
†Email address for correspondence: driesallaerts@gmail.com
Get access Rights & Permissions [Opens in a new window]

Abstract

Flow blockage by large wind farms leads to an upward displacement of the boundary layer, which may excite atmospheric gravity waves in the free atmosphere and on the interface between the boundary layer and the free atmosphere. In the current study, we assess the sensitivity of wind-farm gravity-wave excitation to important dimensionless groups and investigate the feedback of gravity-wave-induced pressure fields to wind-farm energy extraction. The sensitivity analysis is performed using a fast boundary-layer model that is developed to this end. It is based on a three-layer representation of the atmosphere in an idealised barotropic environment, and is coupled with an analytical wake model to account for turbine wake interactions. We first validate the model in two-dimensional mode with data from previous large-eddy simulations of ‘infinitely’ wide wind farms, and then use the model to investigate the sensitivity of wind-farm-induced gravity waves to atmospheric state and wind-farm configuration. We find that the inversion layer induces flow physics similar to shallow-water flow and that the corresponding Froude number plays a crucial role. Gravity-wave excitation is maximal at a critical Froude number equal to one, but the feedback on energy extraction is highest when the Froude number is slightly below one due to a trade-off between amplitude and upstream impact of gravity waves. The effect of surface friction and internal gravity waves is to reduce the flow perturbation and the related power loss by dissipating or dispersing perturbation energy. With respect to the wind-farm configuration, we find that gravity-wave-induced power loss increases with wind-farm size and turbine height. Moreover, we find that gravity-wave effects are small for very wide or very long wind farms and attain a maximum at a width-to-depth ratio of approximately 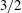$3/2$.

JFM classification

Geophysical and Geological Flows: Atmospheric flows Geophysical and Geological Flows: Internal waves
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 862 , 10 March 2019 , pp. 990 - 1028
Copyright
© 2019 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Allaerts, D. & Meyers, J. 2015 Large eddy simulation of a large wind-turbine array in a conventionally neutral atmospheric boundary layer. Phys. Fluids 27, 065108.Google Scholar
Allaerts, D. & Meyers, J. 2017 Boundary-layer development and gravity waves in conventionally neutral wind farms. J. Fluid Mech. 814, 95–130.Google Scholar
Allaerts, D. & Meyers, J. 2018 Gravity waves and wind-farm efficiency in neutral and stable conditions. Boundary-Layer Meteorol. 166 (2), 269–299.Google Scholar
Annoni, J., Gebraad, P. M. O., Scholbrock, A. K., Fleming, P. A. & van Wingerden, J.-W. 2016 Analysis of axial-induction-based wind plant control using an engineering and a high-order wind plant model. Wind Energy 19 (6), 1135–1150.Google Scholar
Baines, P. G. 1995 Topographic Effects in Stratified Flows. Cambridge University Press.Google Scholar
Baker, A. H., Jessup, E. R. & Manteuffel, T. 2005 A technique for accelerating the convergence of restarted GMRES. SIAM J. Matrix Anal. Applics. 26 (4), 962–984.Google Scholar
Bastankhah, M. & Porté-Agel, F. 2014 A new analytical model for wind-turbine wakes. Renew. Energy 70, 116–123.Google Scholar
Burton, T., Sharpe, D., Jenkins, N. & Bossanyi, E. 2001 Wind Energy Handbook. Wiley.Google Scholar
Canuto, C., Hussaini, M. Y., Quarteroni, A. & Zang, T. A. 1988 Spectral Methods in Fluid Dynamics. Springer.Google Scholar
Chamorro, L. P. & Porté-Agel, F. 2011 Turbulent flow inside and above a wind farm: a wind-tunnel study. Energies 4 (11), 1916–1936.Google Scholar
Csanady, G. T. 1974 Equilibrium theory of the planetary boundary layer with an inversion lid. Boundary-Layer Meteorol. 6 (1–2), 63–79.Google Scholar
Fitch, A. C., Lundquist, J. K. & Olson, J. B. 2013 Mesoscale influences of wind farms throughout a diurnal cycle. Mon. Weath. Rev. 141 (7), 2173–2198.Google Scholar
Fitch, A. C., Olson, J. B., Lundquist, J. K., Dudhia, J., Gupta, A. K., Michalakes, J. & Barstad, I. 2012 Local and mesoscale impacts of wind farms as parameterized in a mesoscale NWP model. Mon. Weath. Rev. 140 (9), 3017–3038.Google Scholar
Gill, A. E. 1982 Atmosphere-Ocean Dynamics, International Geophysics Series, vol. 30. Academic Press.Google Scholar
Hess, G. D. 2004 The neutral, barotropic planetary boundary layer, capped by a low-level inversion. Boundary-Layer Meteorol. 110 (3), 319–355.Google Scholar
Hirsch, C. 1988 Fundamentals of Numerical Discretization, Numerical Computation of Internal and External Flows, vol. 1. Wiley.Google Scholar
Holoborodko, P.2011 Cubature formulas for the unit disk. http://www.holoborodko.com/pavel/numerical-methods/numerical-integration/cubature-formulas-for-the-unit-disk/ accessed 23 March 2018.Google Scholar
van der Laan, M. P. & Sørensen, N. N. 2017 Why the Coriolis force turns a wind farm wake clockwise in the Northern Hemisphere. Wind Energy Sci. 2, 285–294.Google Scholar
Mattheij, R. M. M., Rienstra, S. W. & ten Thije Boonkkamp, J. H. M. 2005 Partial Differential Equations: Modeling, Analysis, Computation. Society for Industrial and Applied Mathematics (SIAM).Google Scholar
Nappo, C. J. 2002 An Introduction to Atmospheric Gravity Waves, International Geophysics Series, vol. 85. Academic Press.Google Scholar
Niayifar, A. & Porté-Agel, F. 2016 Analytical modeling of wind farms: a new approach for power prediction. Energies 9 (9), 741.Google Scholar
Nieuwstadt, F. T. M. 1983 On the solution of the stationary, baroclinic Ekman-layer equations with a finite boundary-layer height. Boundary-Layer Meteorol. 26 (4), 377–390.Google Scholar
Ockendon, J., Howison, S., Lacey, A. & Movchan, A. 1999 Applied Partial Differential Equations. Oxford University Press.Google Scholar
Rampanelli, G. & Zardi, D. 2004 A method to determine the capping inversion of the convective boundary layer. J. Appl. Meteorol. 43 (6), 925–933.Google Scholar
Smith, R. B. 1980 Linear theory of stratified hydrostatic flow past an isolated mountain. Tellus 32 (4), 348–364.Google Scholar
Smith, R. B. 2007 Interacting mountain waves and boundary layers. J. Atmos. Sci. 64, 594–607.Google Scholar
Smith, R. B. 2010 Gravity wave effects on wind farm efficiency. Wind Energy 13 (5), 449–458.Google Scholar
Smith, R. B., Jiang, Q. & Doyle, J. D. 2006 A theory of gravity wave absorption by a boundary layer. J. Atmos. Sci. 63 (2), 774–781.Google Scholar
Sorbjan, Z. 1996 Effects caused by varying the strength of the capping inversion based on a large eddy simulation model of the shear-free convective boundary layer. J. Atmos. Sci. 53 (14), 2015–2024.Google Scholar
Stevens, R. J. A. M., Gayme, D. F. & Meneveau, C. 2016 Effects of turbine spacing on the power output of extended wind-farms. Wind Energy 19, 359–370.Google Scholar
Stull, R. B. 1988 An Introduction to Boundary Layer Meteorology. Springer.Google Scholar
Taylor, J. R. & Sarkar, S. 2008 Stratification effects in a bottom Ekman layer. J. Phys. Oceanogr. 38 (11), 2535–2555.Google Scholar
Tjernström, M. & Smedman, A.-S. 1993 The vertical turbulence structure of the coastal marine atmospheric boundary layer. J. Geophys. Res. Oceans 98 (C3), 4809–4826.Google Scholar
Volker, P. J. H.2014 Wake effects of large offshore wind farms: a study of the mesoscale atmophere. PhD thesis, DTU Wind Energy.Google Scholar
Wu, K. L. & Porté-Agel, F. 2017 Flow adjustment inside and around large finite-size wind farms. Energies 10 (12), 2164.Google Scholar
Wu, Y.-T. & Porté-Agel, F. 2013 Simulation of turbulent flow inside and above wind farms: model validation and layout effects. Boundary-Layer Meteorol. 146 (2), 181–205.Google Scholar
Wyngaard, J. C. 2010 Turbulence in the Atmosphere. Cambridge University Press.Google Scholar