Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-21T19:16:07.794Z Has data issue: false hasContentIssue false
  • English
  • Français

Similarity solutions and viscous gravity current adjustment times

Published online by Cambridge University Press:  04 July 2019

Thomasina V. Ball Open the ORCID record for Thomasina V. Ball [Opens in a new window]  and
Herbert E. Huppert
Thomasina V. Ball
Affiliation:
BP Institute, Department of Earth Sciences, University of Cambridge, Bullard Laboratories, Madingley Road, Cambridge CB3 0EZ, UK
Herbert E. Huppert*
Affiliation:
Institute of Theoretical Geophysics, King’s College, Cambridge CB2 1ST, UK
*
†Email address for correspondence: heh1@cam.ac.uk
Get access Rights & Permissions [Opens in a new window]

Abstract

A wide range of initial-value problems in fluid mechanics in particular, and in the physical sciences in general, are described by nonlinear partial differential equations. Recourse must often be made to numerical solutions, but a powerful, well-established technique is to solve the problem in terms of similarity variables. 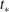A disadvantage of the similarity solution is that it is almost always independent of any specific initial conditions, with the solution to the full differential equation approaching the similarity solution for times $t\gg t_{\ast }$, for some $t_{\ast }$. But what is 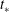$t_{\ast }$? In this paper we consider the situation of viscous gravity currents and obtain useful formulae for the time of approach, 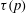$\unicode[STIX]{x1D70F}(p)$, for a number of different initial shapes, where $p$ is the percentage disagreement between the radius of the current as determined by the full numerical solution of the governing partial differential equation and the similarity solution normalised by the similarity solution. We show that for any initial shape of volume $V,\unicode[STIX]{x1D70F}\propto 1/(\unicode[STIX]{x1D6FD}V^{1/3}\unicode[STIX]{x1D6FE}_{0}^{8/3}p)$ (as $p\downarrow 0$), where $\unicode[STIX]{x1D6FD}=g\unicode[STIX]{x0394}\unicode[STIX]{x1D70C}/(3\unicode[STIX]{x1D707})$, with $g$ representing the acceleration due to gravity, $\unicode[STIX]{x0394}\unicode[STIX]{x1D70C}$ the density difference between the gravity current and the ambient, $\unicode[STIX]{x1D707}$ the dynamic viscosity of the fluid that makes up the gravity current and $\unicode[STIX]{x1D6FE}_{0}$ the initial aspect ratio. This framework can used in many other situations, including where it is not an initial condition (in time) that is studied but one valid for specified values at a special spatial coordinate.

JFM classification

Geophysical and Geological Flows: Gravity currents Low-Reynolds-number flows: Lubrication theory
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 874 , 10 September 2019 , pp. 285 - 298
Check for updates
Copyright
© 2019 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Acton, J. M., Huppert, H. E. & Worster, M. G. 2001 Two-dimensional viscous gravity currents flowing over a deep porous medium. J. Fluid Mech. 440, 359–380.Google Scholar
Barenblatt, G. I. 2003 Scaling. Cambridge University Press.Google Scholar
Blake, S. 1990 Viscoplastic models for lava domes. In Lava Domes and Flows, IAVCEI Proceedings in Volcanology (ed. Fink, J. H.), vol. 2, pp. 88–126. Springer.Google Scholar
Dalziel, S. B. & Huppert, H. E. 2019 Instability of an expanding viscous drop in a rapidly rotating system. J. Fluid Mech. (submitted).Google Scholar
Fink, J. H. 1987 The emplacement of silicic domes and lava flows. In GSA Special Papers, vol. 212. Geological Society of America.Google Scholar
Fink, J. H. & Griffiths, R. W. 1990 Radial spreading of viscous gravity currents with solidifying crust. J. Fluid Mech. 221, 485–509.Google Scholar
Grundy, R. E. & Rottman, J. W. 1985 The approach to self-similarity of the solutions of the shallow-water equations representing gravity current releases. J. Fluid Mech. 156, 39–53.Google Scholar
Huppert, H. E. 1982 The propagation of two-dimensional and axisymmetric viscous gravity currents over a rigid horizontal surface. J. Fluid Mech. 121, 43–58.Google Scholar
Huppert, H. E. 2006 Gravity currents: a personal perspective. J. Fluid Mech. 554, 299–322.Google Scholar
Huppert, H. E., Shepherd, J. B., Sigurdsson, H. & Sparks, R. S. J. 1982 On lava dome growth, with application to the 1979 lava extrusion of the Soufriere of St. Vincent. J. Volcanol. Geoth. Res. 14, 199–222.Google Scholar
Huppert, H. E. & Woods, A. W. 1995 Gravity-driven flows in porous layers. J. Fluid Mech. 292, 55–69.Google Scholar
Johnson, C. G., Hogg, A. J., Huppert, H. E., Sparks, R. S., Phillips, J. C., Slim, A. C. & Woodhouse, M. J. 2015 Modelling intrusions through quiescent and moving ambients. J. Fluid Mech. 771, 370–406.Google Scholar
Lyle, S., Huppert, H. E., Hallworth, M., Bickles, M. & Chadwick, A. 2005 Axisymmetric gravity currents in a porous medium. J. Fluid Mech. 543, 293–302.Google Scholar
McKenzie, D. P. 1992 Pancake like domes on Venus. J. Geophys. Res. 97, 15967–15976.Google Scholar
Nye, J. F. 1952 The mechanics of glacier flow. J. Glaciol. 2, 82–93.Google Scholar
Pattle, R. E. 1959 Diffusion from an instantaneous point source with a concentration-dependent co-efficient. Q. J. Mech. Appl. Math. 13, 402–409.Google Scholar
Phillips, O. M. 1991 Flow and Reactions in Permeable Rocks. Cambridge University Press.Google Scholar
Simpson, J. E. 1999 Gravity Currents in the Environment and the Laboratory. Cambridge University Press.Google Scholar
Webber, J. J. & Huppert, H. E. 2019 Time to approach similarity. Q. J. Mech. Appl. Maths (submitted).Google Scholar