Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-22T11:49:20.107Z Has data issue: false hasContentIssue false
  • English
  • Français

Spiralling liquid jets: verifiable mathematical framework, trajectories and peristaltic waves

Published online by Cambridge University Press:  24 April 2017

Yulii D. Shikhmurzaev Open the ORCID record for Yulii D. Shikhmurzaev [Opens in a new window]  and
Grigori M. Sisoev
Yulii D. Shikhmurzaev*
Affiliation:
School of Mathematics, University of Birmingham, Birmingham B15 2TT, UK
Grigori M. Sisoev
Affiliation:
Institute of Mechanics, Lomonosov Moscow State University, Moscow 119192, Russia
*
†Email address for correspondence: Y.D.Shikhmurzaev@bham.ac.uk
Get access Rights & Permissions [Opens in a new window]

Abstract

The dynamics of a jet of an inviscid incompressible liquid spiralling out under the action of centrifugal forces is considered with both gravity and the surface tension taken into account. This problem is of direct relevance to a number of industrial applications, ranging from the spinning disc atomization process to nanofibre formation. The mathematical description of the flow by necessity requires the use of a local curvilinear non-orthogonal coordinate system centred around the jet’s baseline, and we present the general formulation of the problem without assuming that the jet is slender. To circumvent the inconvenience inherent in the non-orthogonality of the local coordinate system, the orthonormal Frenet basis is used in parallel with the local non-orthogonal basis, and the equation of motion, with the velocity considered with respect to the local coordinate system, is projected onto the Frenet basis. The variation of the latter along the baseline is then described by the Frenet equations which naturally brings the baseline’s curvature and torsion into the equations of motion. This technique allows one to handle different line-based non-orthogonal curvilinear coordinate systems in a straightforward and mathematically transparent way. An analysis of the slender-jet approximation that follows the general formulation shows how a set of ordinary differential equations describing the jet’s trajectory can be derived in two cases: 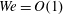$\mathit{We}=O(1)$ and 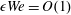$\unicode[STIX]{x1D716}\mathit{We}=O(1)$ as 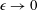$\unicode[STIX]{x1D716}\rightarrow 0$, where $\unicode[STIX]{x1D716}$ is the ratio of characteristic length scales across and along the jet and 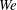$\mathit{We}$ is the Weber number. A one-dimensional model for the propagation of nonlinear peristaltic disturbances along the jet is derived in each of these cases. A critical review of the work published on this topic is presented showing where errors typically occur and how to identify and avoid them.

JFM classification

Interfacial Flows (free surface): Capillary flows Interfacial Flows (free surface): Interfacial Flows (free surface)
Type
Papers
Information
Journal of Fluid Mechanics , Volume 819 , 25 May 2017 , pp. 352 - 400
Check for updates
Copyright
© 2017 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Alsharif, A. M., Uddin, J. & Afzaal, M. F. 2015 Instability of viscoelastic curved liquid jets. Appl. Math. Modell. 39, 3924–3938.Google Scholar
Butenin, N. V., Lunz, Ya. L. & Merkin, D. R. 1979 A Course of Theoretical Mechanics, vol. 2. Nauka.Google Scholar
Cummings, L. J. & Howell, P. D. 1999 On the evolution of non-axisymmetric viscous fibres with surface tension, inertia and gravity. J. Fluid Mech. 389, 361–389.Google Scholar
Decent, S. P., King, A. C., Simmons, M. J. H., Părău, E. I., Wallwork, I. M., Gurney, C. J. & Uddin, J. 2009 The trajectory and stability of a spiralling liquid jet: viscous theory. Appl. Math. Modell. 33, 4283–4302.Google Scholar
Decent, S. P., King, A. C. & Wallwork, I. M. 2002 Free jets spun from a prilling tower. J. Engng Maths 42, 265–282.CrossRefGoogle Scholar
Dewynne, J. N., Ockendon, J. R. & Wilmott, P. 1992 A systematic derivation of the leading-order equations for extensional flows in slender geometries. J. Fluid Mech. 244, 323–338.Google Scholar
Entov, V. M. & Yarin, A. L. 1984 The dynamics of thin liquid jets in air. J. Fluid Mech. 140, 91–111.Google Scholar
Frost, A. R. 1981 Rotary atomization in the ligament formation mode. J. Agric. Engng Res. 26, 63–78.Google Scholar
Garcia, F. J. & Castellanos, A. 1994 One-dimensional models for slender axisymmetric viscous liquid jets. Phys. Fluids 6, 2676–2689.CrossRefGoogle Scholar
Green, A. E. & Zerna, W. 1992 Theoretical Elasticity. Dover.Google Scholar
Hawkins, V. L., Gurney, C. J., Decent, S. P., Simmons, M. J. H. & Uddin, J. 2010 Unstable waves on a curved non-Newtonian liquid jet. J. Phys. A: Math. Theor. 43, 055501.Google Scholar
Korn, G. A. & Korn, T. M. 1968 Mathematical Handbook for Scientists and Engineers. McGraw-Hill.Google Scholar
Lin, S. P. & Webb, R. 1994 Non-axisymmetric evanescent waves in a viscous liquid jet. Phys. Fluids 6, 2545–2547.Google Scholar
Marheineke, N., Liljegren-Sailer, B., Lorenz, M. & Wegener, R. 2016 Asymptotics and numerics for the upper-convected maxwell model describing transient curved viscoelastic jets. Math. Models Meth. Appl. Sci. 26, 569–600.Google Scholar
Marheineke, N. & Wegener, R. 2009 Asymptotic model for the dynamics of curved viscous figres with surface tension. J. Fluid Mech. 622, 345–369.Google Scholar
Markova, M. P. & Shkadov, V. Ya. 1972 Nonlinear development of capillary waves in a liquid jet. Fluid Dyn. 7 (3), 392–398.Google Scholar
Mellado, P., McIlwee, H. A. & Badrossamay, M. A. 2011 A simple model for nanofibre formation by rotary jet-spinning. Appl. Phys. Lett. 99, 203107.Google Scholar
Panda, S., Marheineke, N. & Wegener, R. 2008 Systematic derivation of an asymptotic model for the dynamics of curved viscous fibers. Math. Meth. Appl. Sci. 31, 1153–1173.Google Scholar
Papageorgiou, D. T. & Orellana, O. 1998 Study of cylindrical jet breakup using one-dimensional approximations of the euler equations. SIAM J. Appl. Maths 59, 286–317.Google Scholar
Părău, E. I., Decent, S. P., King, A. C., Simmons, M. J. H. & Wong, D. C. Y. 2006 Nonlinear travelling waves on a spiralling liquid jet. Wave Motion 43, 599–618.Google Scholar
Părău, E. I., Decent, S. P., Simmons, M. J. H., Wong, D. C. Y. & King, A. C. 2007 Nonlinear viscous liquid jets from a rotating orifice. J. Engng Maths 57, 159–179.Google Scholar
Partridge, L., Wong, D. C. Y., Simmons, M. J. H., Părău, E. I. & Decent, S. P. 2005 Experimental and theoretical description of the break-up of curved liquid jets in the prilling process. Chem. Engng Res. Des. 83, 1267–1275.CrossRefGoogle Scholar
Pearson, J. R. A. 1985 Mechanics of Polymer Processing. Applied Science Publishers.Google Scholar
Ribe, N. M. 2004 Coiling of viscous jets. Proc. R. Soc. Lond. A 460, 3223–3239.CrossRefGoogle Scholar
Saleh, S. N., Ahmed, S. M., Al-Mosuli, D. & Barghi, S. 2015 Basic design methodology for a prilling tower. Can. J. Chem. Engng 93, 1403–1409.CrossRefGoogle Scholar
Sedov, L. I. 1997 Mechanics of Continuous Media, vol. 1. World Scientific.Google Scholar
Senuma, S., Lowe, C., Zweifel, Y., Hilborn, J. G. & Marison, I. 2000 Alginate hydrogelmicrospheres and microcapsules prepared by spinning disk atomization. Biotechnol. Bioeng. 67, 616–622.Google Scholar
Shikhmurzaev, Y. D. 1997 Spreading of drops on solid surfaces in a quasi-static regime. Phys. Fluids 9, 266–275.Google Scholar
Tchavdarov, B., Yarin, A. L. & Radev, S. 1993 Buckling of thin liquid jets. J. Fluid Mech. 253, 593–615.Google Scholar
Ting, L. & Keller, J. B. 1990 Slender jets and thin sheets with surface tension. SIAM J. Appl. Maths 50, 1533–1546.Google Scholar
Uddin, J. & Decent, S. P. 2009 Curved non-Newtonian liquid jets with surfactants. J. Fluids Engng 131, 091203.Google Scholar
Uddin, J. & Decent, S. P. 2012 Drop formation in rotating non-Newtonian jets with surfactants. IMA J. Appl. Maths 77, 86–96.Google Scholar
Uddin, J., Decent, S. P. & Simmons, M. J. 2006 The instability of shear thinning and shear thickening spiralling liquid jets: linear theory. J. Fluids Engng 128, 968–975.CrossRefGoogle Scholar
Uddin, J., Decent, S. P. & Simmons, M. J. H. 2008 The effect of surfactants on the instability of a rotating liquid jet. Fluid Dyn. Res. 40, 827–851.CrossRefGoogle Scholar
Wallwork, I. M., Decent, S. P., King, A. C. & Schulkes, R. M. S. M. 2002 The trajectory and stability of a spiralling liquid jet: Part 1. Inviscid theory. J. Fluid Mech. 459, 43–65.Google Scholar
Zhang, X. & Lu, A. 2014 Centrifugal spinning: an alternative approach to fabricate nanofibres at high speed and low cost. Polymer Rev. 54, 677–701.Google Scholar