Hostname: page-component-586b7cd67f-vdxz6 Total loading time: 0 Render date: 2024-11-28T09:53:28.746Z Has data issue: false hasContentIssue false
  • English
  • Français

Stability of three-dimensional Gaussian vortices in an unbounded, rotating, vertically stratified, Boussinesq flow: linear analysis

Published online by Cambridge University Press:  05 July 2017

Mani Mahdinia ,
Pedram Hassanzadeh Open the ORCID record for Pedram Hassanzadeh [Opens in a new window] ,
Philip S. Marcus  and
Chung-Hsiang Jiang
Mani Mahdinia
Affiliation:
Department of Mechanical Engineering, University of California, Berkeley, CA 94720, USA
Pedram Hassanzadeh
Affiliation:
Department of Mechanical Engineering, Rice University, Houston, TX 77005, USA Center for the Environment and Department of Earth and Planetary Sciences, Harvard University, Cambridge, MA 02138, USA
Philip S. Marcus*
Affiliation:
Department of Mechanical Engineering, University of California, Berkeley, CA 94720, USA
Chung-Hsiang Jiang
Affiliation:
Department of Mechanical Engineering, University of California, Berkeley, CA 94720, USA
*
†Email address for correspondence: pmarcus@me.berkeley.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

The linear stability of three-dimensional vortices in rotating, stratified flows has been studied by analysing the non-hydrostatic inviscid Boussinesq equations. We have focused on a widely used model of geophysical and astrophysical vortices, which assumes an axisymmetric Gaussian structure for pressure anomalies in the horizontal and vertical directions. For a range of Rossby numbers (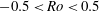$-0.5<Ro<0.5$) and Burger numbers (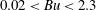$0.02<Bu<2.3$) relevant to observed long-lived vortices, the growth rate and spatial structure of the most unstable eigenmodes have been numerically calculated and presented as a function of 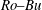$Ro{-}Bu$. We have found neutrally stable vortices only over a small region of the 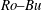$Ro{-}Bu$ parameter space: cyclones with 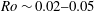$Ro\sim 0.02{-}0.05$ and 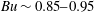$Bu\sim 0.85{-}0.95$. However, we have also found that anticyclones in general have slower growth rates compared to cyclones. In particular, the growth rate of the most unstable eigenmode for anticyclones in a large region of the parameter space (e.g. 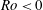$Ro<0$ and 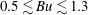$0.5\lesssim Bu\lesssim 1.3$) is slower than 50 turnaround times of the vortex (which often corresponds to several years for ocean eddies). For cyclones, the region with such slow growth rates is confined to 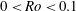$0<Ro<0.1$ and 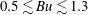$0.5\lesssim Bu\lesssim 1.3$. While most calculations have been done for 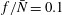$f/\bar{N}=0.1$ (where 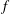$f$ and 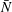$\bar{N}$ are the Coriolis and background Brunt–Väisälä frequencies), we have numerically verified and explained analytically, using non-dimensionalized equations, the insensitivity of the results to reducing 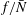$f/\bar{N}$ to the more ocean-relevant value of 0.01. The results of our stability analysis of Gaussian vortices both support and contradict the findings of earlier studies with QG or multilayer models or with other families of vortices. The results of this paper provide a stepping stone to study the more complicated problems of the stability of geophysical (e.g. those in the atmospheres of giant planets) and astrophysical vortices (in accretion disks).

JFM classification

Geophysical and Geological Flows: Geophysical and Geological Flows Geophysical and Geological Flows: Ocean processes Vortex Flows: Vortex instability
Type
Papers
Information
Journal of Fluid Mechanics , Volume 824 , 10 August 2017 , pp. 97 - 134
Check for updates
Copyright
© 2017 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Armi, L., Hebert, D., Oakey, N., Price, J., Richardson, P. L., Rossby, T. & Ruddick, B. 1988 The history and decay of a Mediterranean salt lens. Nature 333, 649–651.Google Scholar
Armi, L., Hebert, D., Oakey, N., Price, J. F., Richardson, P. L., Rossby, H. T. & Ruddick, B. 1989 Two years in the life of a Mediterranean salt lens. J. Phys. Oceanogr. 19, 354–370.2.0.CO;2>CrossRefGoogle Scholar
Aubert, O., Le Bars, M., Le Gal, P. & Marcus, P. S. 2012 The universal aspect ratio of vortices in rotating stratfied flows: experiments and observations. J. Fluid Mech. 706, 34–45.Google Scholar
Baey, J.-M. & Carton, X. 2002 Vortex multipoles in two-layer rotating shallow-water flows. J. Fluid Mech. 460, 151–175.Google Scholar
Barcilon, V. & Pedlosky, J. 1967 On the steady motions produced by a stable stratification in a rapidly rotating fluid. J. Fluid Mech. 29, 673–690.CrossRefGoogle Scholar
Barge, P. & Sommeria, J. 1995 Did planet formation begin inside persistent gaseous vortices? Astron. Astrophys. 295, L1–L4.Google Scholar
Barranco, J. A. & Marcus, P. S. 2005 Three-dimensional vortices in stratified protoplanetary disks. Astrophys. J. 623, 1157–1170.CrossRefGoogle Scholar
Barranco, J. A. & Marcus, P S. 2006 A 3D spectral anelastic hydrodynamic code for shearing, stratified flows. J. Comput. Phys. 219, 21–46.CrossRefGoogle Scholar
Bashmachnikov, I., Neves, F., Calheiros, T. & Carton, X. 2015 Properties and pathways of Mediterranean water eddies in the Atlantic. Prog. Oceanogr. 137, 149–172.CrossRefGoogle Scholar
Benilov, E. S. 2003 Instability of quasi-geostrophic vortices in a two-layer ocean with a thin upper layer. J. Fluid Mech. 475, 303–331.Google Scholar
Benilov, E. S. 2004 Stability of vortices in a two-layer ocean with uniform potential vorticity in the lower layer. J. Fluid Mech. 502, 207–232.CrossRefGoogle Scholar
Benilov, E. S. 2005a The effect of ageostrophy on the stability of thin oceanic vortices. Dyn. Atmos. Oceans 39, 211–226.Google Scholar
Benilov, E. S. 2005b On the stability of oceanic vortices: A solution to the problem? Dyn. Atmos. Oceans 40, 133–149.CrossRefGoogle Scholar
Benilov, E. S., Broutman, D. & Kuznetsova, E. P. 1998 On the stability of large-amplitude vortices in a continuously stratified fluid on the f-plane. J. Fluid Mech. 355, 139–162.Google Scholar
Benilov, E. S. & Flanagan, J. D. 2008 The effect of ageostrophy on the stability of vortices in a two-layer ocean. Ocean Model. 23, 49–58.Google Scholar
Billant, P., Dritschel, D. G. & Chomaz, J.-M. 2006 Bending and twisting instabilities of columnar elliptical vortices in a rotating strongly stratified fluid. J. Fluid Mech. 561, 73–102.Google Scholar
Brunner-Suzuki, A. E. G., Sundermeyer, M. A. & Lelong, M. P. 2012 Vortex stability in a large-scale internal wave shear. J. Phys. Oceanogr. 42, 1668–1683.Google Scholar
Carton, X. 2001 Hydrodynamical modeling of oceanic vortices. Surv. Geophys. 22, 179–263.Google Scholar
Carton, X. J. & McWilliams, J. C. 1989 Barotropic and baroclinic instabilities of axisymmetric vortices in a quasigeostrophic model. In Mesoscale/Synoptic Coherent Structures in Geophysical Turbulence (ed. Nihoul, J. C. J. & Jamart, B. M.), pp. 225–244. Elsevier.Google Scholar
Chang, K.-I., Teague, W. J., Lyu, S. J., Perkins, H. T., Lee, D.-K., Watts, D. R., Kim, Y.-B., Mitchell, D. A., Lee, C. M. & Kim, K. 2004 Circulation and currents in the southwestern East/Japan Sea: overview and review. Prog. Oceanogr. 61, 105–156.Google Scholar
Chelton, D. B., deSzoeke, R. A. & Schlax, M. G. 1998 Geographical variability of the first baroclinic Rossby radius of deformation. J. Phys. Oceanogr. 28, 433–460.Google Scholar
Chelton, D. B., Schlax, M. G. & Samelson, R. M. 2011 Global observations of nonlinear mesoscale eddies. Prog. Oceanogr. 91, 167–216.CrossRefGoogle Scholar
Chelton, D. B., Schlax, M. G., Samelson, R. M. & de Szoeke, R. A. 2007 Global observations of large oceanic eddies. Geophys. Res. Lett. 34, L15606.CrossRefGoogle Scholar
Cho, J. Y. K. & Polvani, L. M. 1996 The morphogenesis of bands and zonal winds in the atmospheres on the giant outer planets. Science 273, 335–337.CrossRefGoogle ScholarPubMed
D’Asaro, E., Walker, S. & Baker, E. 1994 Structure of two hydrothermal megaplumes. J. Geophys. Res. 99, 20361–20373.Google Scholar
Dewar, W. K. & Killworth, P. D. 1995 On the stability of oceanic rings. J. Phys. Oceanogr. 25, 1467–1487.2.0.CO;2>CrossRefGoogle Scholar
Dewar, W. K., Killworth, P. D. & Blundell, J. R. 1999 Primitive-equation instability of wide oceanic rings. Part II. Numerical studies of ring stability. J. Phys. Oceanogr. 29, 1744–1758.Google Scholar
Dong, C., McWilliams, J. C., Liu, Y. & Chen, D. 2014 Global heat and salt transports by eddy movement. Nat. Commun. 5, 3294.CrossRefGoogle ScholarPubMed
Drazin, P. G. & Reid, W. H. 2004 Hydrodynamic Stability. Cambridge University Press.Google Scholar
Dritschel, D. G. & Mckiver, W. J. 2015 Effect of Prandtl’s ratio on balance in geophysical turbulence. J. Fluid Mech. 777, 569–590.CrossRefGoogle Scholar
Ertel, H. 1942 Ein neuer hydrodynamischer wirbelsatz. Meteorol. Z. 59, 277–281.Google Scholar
Flierl, G. R. 1988 On the instability of geostrophic vortices. J. Fluid Mech. 197, 349–388.CrossRefGoogle Scholar
Gascard, J.-C., Watson, A. J., Messias, M.-J., Olsson, K. A., Johannessen, T. & Simonsen, K. 2002 Long-lived vortices as a mode of deep ventilation in the Greenland Sea. Nature 416, 525–527.Google Scholar
Gent, P. R. & McWilliams, J. C. 1986 The instability of barotropic circular vortices. Geophys. Astro. Fluid 35, 209–233.Google Scholar
Graves, L. P., McWilliams, J. C. & Montgomery, M. T. 2006 Vortex evolution due to straining: a mechanism for dominance of strong, interior anticyclones. Geophys. Astro. Fluid 100, 151–183.CrossRefGoogle Scholar
Hassanzadeh, P. & Kuang, Z. 2015 Blocking variability: arctic amplification versus arctic oscillation. Geophys. Res. Lett. 42, 8586–8595.Google Scholar
Hassanzadeh, P., Kuang, Z. & Farrell, B. F. 2014 Responses of midlatitude blocks and wave amplitude to changes in the meridional temperature gradient in an idealized dry GCM. Geophys. Res. Lett. 41, 5223–5232.Google Scholar
Hassanzadeh, P., Marcus, P. S. & Le Gal, P. 2012 The universal aspect ratio of vortices in rotating stratified flows: theory and simulation. J. Fluid Mech. 706, 46–57.CrossRefGoogle Scholar
Hebert, D., Oakey, N. & Ruddick, B. 1990 Evolution of a mediterranean salt lens: scalar properties. J. Phys. Oceanogr. 20, 1468–1483.Google Scholar
van Heijst, G. J. F. & Clercx, H. J. H. 2009 Laboratory modeling of geophysical vortices. Annu. Rev. Fluid Mech. 41, 143–164.Google Scholar
Helfrich, K. R. & Send, U. 1988 Finite-amplitude evolution of two-layer geostrophic vortices. J. Fluid Mech. 197, 331–348.Google Scholar
Hoskins, B. J., Mcintyre, M. E. & Robertson, A. W. 1985 On the use and significance of isentropic potential vorticity maps. Q. J. R. Meteorol. Soc. 111, 877–946.Google Scholar
Ikeda, M. 1981 Instability and splitting of mesoscale rings using a two-layer quasi-geostrophic model on an f-plane. J. Phys. Oceanogr. 11, 987–998.Google Scholar
Katsman, C. A., Van der Vaart, P. C. F., Dijkstra, H. A. & De Ruijter, W. P. M. 2003 Stability of multilayer ocean vortices: a parameter study including realistic Gulf stream and Agulhas rings. J. Phys. Oceanogr. 33, 1197–1218.2.0.CO;2>CrossRefGoogle Scholar
Killworth, P. D., Blundell, J. R. & Dewar, W. K. 1997 Primitive equation instability of wide oceanic rings. Part I. Linear theory. J. Phys. Oceanogr. 27, 941–962.2.0.CO;2>CrossRefGoogle Scholar
Lahaye, N. & Zeitlin, V. 2015 Centrifugal, barotropic and baroclinic instabilities of isolated ageostrophic anticyclones in the two-layer rotating shallow water model and their nonlinear saturation. J. Fluid Mech. 762, 5–34.Google Scholar
Lai, D. Y. & Richardson, P. L. 1977 Distribution and movement of Gulf Stream rings. J. Phys. Oceanogr. 7, 670–683.Google Scholar
Lazar, A., Stegner, A., Caldeira, R., Dong, C., Didelle, H. & Viboud, S. 2013a Inertial instability of intense stratified anticyclones. Part 2. Laboratory experiments. J. Fluid Mech. 732, 485–509.Google Scholar
Lazar, A., Stegner, A. & Heifetz, E. 2013b Inertial instability of intense stratified anticyclones. Part 1. Generalized stability criterion. J. Fluid Mech. 732, 457–484.CrossRefGoogle Scholar
Lelong, M.-P. & Sundermeyer, M. A. 2005 Geostrophic adjustment of an osolated diapycnal mixing event and its implications for small-scale lateral dispersion. J. Phys. Oceanogr. 35, 2352–2367.Google Scholar
Mac Low, M.-M. & Ingersoll, A. P. 1986 Merging of vortices in the atmosphere of Jupiter: An analysis of Voyager images. Icarus 65, 353–369.Google Scholar
Marcus, P. S. 1993 Jupiter’s Great Red Spot and other vortices. Annu. Rev. Astron. Astrophys. 31, 523–573.Google Scholar
Marcus, P. S. 2004 Prediction of a global climate change on Jupiter. Nature 428, 828–831.CrossRefGoogle ScholarPubMed
Marcus, P. S. & Hassanzadeh, P. 2014 On the surprising longevity of Jupiter’s centuries-old Great Red Spot. In APS Meeting Abstracts, 67th Annual Meeting of the APS Division of Fluid Dynamics.Google Scholar
Marcus, P. S., Pei, S., Jiang, C.-H., Barranco, J. A., Hassanzadeh, P. & Lecoanet, D. 2015 Zombie vortex instability. I. A purely hydrodynamic instability to resurrect the dead zones of protoplanetary disks. Astrophys. J. 808, 87.CrossRefGoogle Scholar
Marcus, P. S., Pei, S., Jiang, C.-H. & Hassanzadeh, P. 2013 Three-dimensional vortices generated by self-replication in stably stratified rotating shear flows. Phys. Rev. Lett. 111, 084501.CrossRefGoogle ScholarPubMed
Maslowe, S. A. 1986 Critical layers in shear flows. Annu. Rev. Fluid Mech. 18, 405–432.Google Scholar
Matsushima, T. & Marcus, P. S. 1995 A spectral method for polar coordinates. J. Comput. Phys. 120, 365–374.Google Scholar
Matsushima, T. & Marcus, P. S. 1997 A spectral method for unbounded domains. J. Comput. Phys. 137, 321–345.Google Scholar
McWilliams, J. C. 1985 Submesoscale, coherent vortices in the ocean. Rev. Geophys. 23, 165–182.Google Scholar
Meschanov, S. L. & Shapiro, G. I. 1998 A young lens of Red Sea Water in the Arabian Sea. Deep-Sea Res. I 45, 1–13.CrossRefGoogle Scholar
Mkhinini, N., Coimbra, A. L. S., Stegner, A., Arsouze, T., Taupier-Letage, I. & Béranger, K. 2014 Long-lived mesoscale eddies in the eastern Mediterranean Sea: analysis of 20 years of AVISO geostrophic velocities. J. Geophys. Res. 119, 8603–8626.Google Scholar
Morel, Y. & McWilliams, J. 1997 Evolution of isolated interior vortices in the ocean. J. Phys. Oceanogr. 27, 727–748.Google Scholar
Negretti, M. E. & Billant, P. 2013 Stability of a Gaussian pancake vortex in a stratified fluid. J. Fluid Mech. 718, 457–480.Google Scholar
Nguyen, H. Y., Hua, B. L., Schopp, R. & Carton, X. 2012 Slow quasigeostrophic unstable modes of a lens vortex in a continuously stratified flow. Geophys. Astro. Fluid 106, 305–319.Google Scholar
Olson, D. B. 1991 Rings in the ocean. Annu. Rev. Earth Planet. Sci. 19, 283–311.Google Scholar
O’Neill, M. E., Emanuel, K. A. & Flierl, G. R. 2015 Polar vortex formation in giant-planet atmospheres due to moist convection. Nature Geosci. 8, 523–526.Google Scholar
Ozorio de Almeida, A. M. 1988 Hamiltonian Systems: Chaos and Quantization. Cambridge University Press.Google Scholar
Paillet, J., Le Cann, B., Carton, X., Morel, Y. & Serpette, A. 2002 Dynamics and evolution of a northern meddy. J. Phys. Oceanogr. 32, 55–79.Google Scholar
Perret, G., Dubos, T. & Stegner, A. 2011 How large-scale and cyclogeostrophic barotropic instabilities favor the formation of anticyclonic vortices in the ocean. J. Phys. Oceanogr. 41, 303–328.CrossRefGoogle Scholar
Pingree, R. D. & Le Cann, B. 1993 Structure of a meddy (Bobby 92) southeast of the Azores. Deep-Sea Res. I 40, 2077–2103.Google Scholar
Prater, M. D. & Sanford, T. B. 1994 A meddy off Cape St. Vincent. Part I. Description. J. Phys. Oceanogr. 24, 1572–1586.Google Scholar
Press, W. H., Teukolsky, S. A., Vetterling, W. T. & Flannery, B. P. 2007 Numerical Recipes: The Art of Scientific Computing. Cambridge University Press.Google Scholar
Smyth, W. D. & McWilliams, J. C. 1998 Instability of an axisymmetric vortex in a stably stratified, rotating environment. Theor. Comput. Fluid Dyn. 11, 305–322.Google Scholar
Stegner, A. & Dritschel, D. G. 2000 A numerical investigation of the stability of isolated shallow water vortices. J. Phys. Oceanogr. 30, 2562–2573.Google Scholar
Sundermeyer, M. A. & Lelong, M.-P. 2005 Numerical simulations of lateral dispersion by the relaxation of diapycnal mixing events. J. Phys. Oceanogr. 35, 2368–2386.CrossRefGoogle Scholar
Sutyrin, G. 2015 Why compensated cold-core rings look stable. Geophys. Res. Lett. 42, 5395–5402.Google Scholar
Tsang, Y.-K. & Dritschel, D. G. 2015 Ellipsoidal vortices in rotating stratified fluids: beyond the quasi-geostrophic approximation. J. Fluid Mech. 762, 196–231.Google Scholar
Tuckerman, L. S. & Barkley, D. 1988 Global bifurcation to traveling waves in axisymmetric convection. Phys. Rev. Lett. 61, 408–411.CrossRefGoogle ScholarPubMed
Tyrlis, E. & Hoskins, B. J. 2008 Aspects of a Northern hemisphere atmospheric blocking climatology. J. Atmos. Sci. 65, 1638–1652.Google Scholar
Vallis, G. K. 2006 Atmospheric and Oceanic Fluid Dynamics: Fundamentals and Large-Scale Circulation. Cambridge University Press.Google Scholar
Vasavada, A. R. & Showman, A. P. 2005 Jovian atmospheric dynamics: an update after Galileo and Cassini. Rep. Prog. Phys. 68, 1935–1996.Google Scholar
Yim, E. & Billant, P. 2015 On the mechanism of the Gent–McWilliams instability of a columnar vortex in stratified rotating fluids. J. Fluid Mech. 780, 5–44.Google Scholar
Yim, E., Billant, P. & Ménesguen, C. 2016 Stability of an isolated pancake vortex in continuously stratified-rotating fluids. J. Fluid Mech. 801, 508–553.Google Scholar