Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-23T04:01:32.165Z Has data issue: false hasContentIssue false
  • English
  • Français

Taylor bubble rising in a vertical pipe against laminar or turbulent downward flow: symmetric to asymmetric shape transition

Published online by Cambridge University Press:  20 August 2014

Jean Fabre  and
Bernardo Figueroa-Espinoza
Jean Fabre*
Affiliation:
Institut de Mécanique des Fluides, Institut National Polytechnique de Toulouse, Allée du Professeur Camille Soula, 31400 Toulouse, France
Bernardo Figueroa-Espinoza
Affiliation:
Instituto de Ingeniería, Universidad Nacional Autónoma de México, Calle 21 No. 97A, Colonia Itzimná, 97100, Mérida, Mexico
*
†Email address for correspondence: Jean.Fabre@imft.fr
Get access Rights & Permissions [Opens in a new window]

Abstract

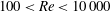The symmetry of Taylor bubbles moving in a vertical pipe is likely to break when the liquid flows downward at a velocity greater than some critical value. The present experiments performed in the inertial regime for Reynolds numbers in the range $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}100<\mathit{Re} < 10\, 000$ show that bifurcation to an eccentric motion occurs, with a noticeable increase of the bubble velocity. The influence of the surface tension parameter (an inverse Eötvös number), 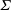$\varSigma $, has been investigated for 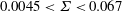$0.0045<\varSigma <0.067$. It appears that the motion of an asymmetric bubble is much more sensitive to surface tension than that of a symmetric bubble. For any given 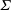$\varSigma $, the symmetry-breaking bifurcation occurs in both laminar and turbulent flow at the same vorticity-to-radius ratio 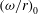${(\omega /r)}_0$ on the axis of the carrier fluid. This conclusion also applies to results obtained previously from numerical experiments in plane flows.

JFM classification

Drops and Bubbles: Bubble dynamics Drops and Bubbles: Drops and Bubbles
Type
Papers
Information
Journal of Fluid Mechanics , Volume 755 , 25 September 2014 , pp. 485 - 502
Copyright
© 2014 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Batchelor, G. K. 1987 The stability of a large gas bubble rising through liquid. J. Fluid Mech. 184, 399–422.CrossRefGoogle Scholar
Bendiksen, K. H. 1985 On the motion of long bubbles in vertical tubes. Intl J. Multiphase Flow 11, 797–812.CrossRefGoogle Scholar
Canny, J. 1986 A computational approach to edge detection. IEEE Trans. Pattern Anal. Mach. Intell. 8 (6), 679–698.CrossRefGoogle ScholarPubMed
Collins, R., de Moraes, F., Davidson, J. F. & Harrison, D. 1978 The motion of large bubbles rising through liquid flowing in a tube. J. Fluid Mech. 89, 497–514.CrossRefGoogle Scholar
Fabre, J. & Liné, A. 1992 Modeling of two-phase slug flow. Annu. Rev. Fluid Mech. 24, 21–46.CrossRefGoogle Scholar
Figueroa-Espinoza, B. & Fabre, J. 2011 Taylor bubble moving in a flowing liquid in vertical channel: transition from symmetric to asymmetric shape. J. Fluid Mech. 679, 432–454.CrossRefGoogle Scholar
Griffith, P. & Wallis, G. B. 1961 Two phase slug flow. Trans. ASME: J. Heat Transfer 83, 307–320.CrossRefGoogle Scholar
Ha Ngoc, H. & Fabre, J. 2004 The velocity and shape of 2D long bubbles in inclined channels or in vertical tubes. Part II: in a flowing liquid. Multiphase Sci. Technol. 16 (1–3), 189–204.Google Scholar
Ha Ngoc, H. & Fabre, J. 2006 A boundary element method for calculating the shape and velocity of two-dimensional long bubble in stagnant and flowing liquid. Engng Anal. Bound. Elem. 30, 539–552.CrossRefGoogle Scholar
Harper, J. F. 1970 On bubbles rising in line at large Reynolds numbers. J. Fluid Mech. 41 (4), 751–758.CrossRefGoogle Scholar
Lu, X. & Prosperetti, A. 2006 Axial stability of Taylor bubbles. J. Fluid Mech. 568, 173–192.CrossRefGoogle Scholar
Magnaudet, J., Rivero, M. & Fabre, J. 1995 Accelerated flows past a rigid sphere or a spherical bubble. Part I: steady straining flow. J. Fluid Mech. 284, 97–135.CrossRefGoogle Scholar
Martin, C. S. 1976 Vertically downward two-phase slug flow. Trans. ASME J. Fluids Engng 98, 715–722.CrossRefGoogle Scholar
Maxworthy, T. 1986 Bubble formation, motion and interaction in a Hele-Shaw cell. J. Fluid Mech. 173, 95–114.CrossRefGoogle Scholar
Nicklin, D. J., Wilkes, J. O. & Davidson, J. F. 1962 Two phase flow in vertical tubes. Trans. Inst. Chem. Engrs 40, 61–68.Google Scholar

Fabre and Bernardo Figueroa-Espinoza suplementary movie

Shape and velocity of Taylor bubble in downward flow: water-glycerol mixture (5.6 cP viscosity and 56 mN/m surface tension) and 40 mm diameter pipe.

Download Fabre and Bernardo Figueroa-Espinoza suplementary movie(Video)
Video 4.3 MB

Fabre and Bernardo Figueroa-Espinoza suplementary movie

Shape and velocity of Taylor bubble in downward flow: water (1 cP viscosity and 72 mN/m surface tension) and 80 mm diameter pipe.

Download Fabre and Bernardo Figueroa-Espinoza suplementary movie(Video)
Video 12.1 MB