Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Kowal, Katarzyna N.
and
Davis, Stephen H.
2019.
Strong shear-flow modulation of instabilities in rapid directional solidification.
Acta Materialia,
Vol. 164,
Issue. ,
p.
464.
Lappa, Marcello
2019.
On the gravitational suppression of hydrothermal modes in liquid layers with a blockage on the bottom wall.
International Journal of Thermal Sciences,
Vol. 145,
Issue. ,
p.
105987.
Yu, Jia-Jia
Li, You-Rong
Ruan, Deng-Fang
and
Wu, Chun-Mei
2019.
Aspect ratio and capillary ratio dependence of thermal-solutal capillary-buoyancy flow of a binary mixture in an annular pool.
International Journal of Thermal Sciences,
Vol. 136,
Issue. ,
p.
347.
Kowal, Katarzyna N.
Davis, Stephen H.
and
Voorhees, Peter W.
2019.
Surface deformations in dynamic thermocapillary convection under partial slip.
Physical Review E,
Vol. 100,
Issue. 2,
Patne, Ramkarn
Agnon, Yehuda
and
Oron, Alexander
2020.
Marangoni instability in the linear Jeffreys fluid with a deformable surface.
Physical Review Fluids,
Vol. 5,
Issue. 8,
Patne, Ramkarn
Agnon, Yehuda
and
Oron, Alexander
2020.
Thermocapillary instabilities in a liquid layer subjected to an oblique temperature gradient: Effect of a prescribed normal temperature gradient at the substrate.
Physics of Fluids,
Vol. 32,
Issue. 11,
Moatimid, Galal M.
Amer, Mohamed F. E.
and
Mohamed, Mona A. A.
2021.
Electrohydrodynamic Instability of a Cylindrical Interface: Effect of the Buoyancy Thermo-Capillary in Porous Media.
Microgravity Science and Technology,
Vol. 33,
Issue. 4,
Chen, Enhui
and
Xu, Feng
2021.
Transient Marangoni convection induced by an isothermal sidewall of a rectangular liquid pool.
Journal of Fluid Mechanics,
Vol. 928,
Issue. ,
Patne, Ramkarn
Agnon, Yehuda
and
Oron, Alexander
2021.
Thermocapillary instability in a viscoelastic liquid layer under an imposed oblique temperature gradient.
Physics of Fluids,
Vol. 33,
Issue. 1,
Patne, Ramkarn
Agnon, Yehuda
and
Oron, Alexander
2021.
Thermocapillary instabilities in a liquid layer subjected to an oblique temperature gradient.
Journal of Fluid Mechanics,
Vol. 906,
Issue. ,
Hu, Kai-Xin
Zhao, Cheng-Zhuo
Zhang, Shao-Neng
and
Chen, Qi-Sheng
2021.
Instabilities of thermocapillary liquid layers with two free surfaces.
International Journal of Heat and Mass Transfer,
Vol. 173,
Issue. ,
p.
121217.
Patne, Ramkarn
and
Oron, Alexander
2022.
Buoyancy instabilities in a liquid layer subjected to an oblique temperature gradient.
Journal of Fluid Mechanics,
Vol. 937,
Issue. ,
HU, Penghui
and
HU, Kaixin
2023.
Instability of Viscoelastic Thermocapillary Liquid Layers with Two Free Surfaces.
Chinese Journal of Space Science,
Vol. 43,
Issue. 4,
p.
683.
Agrawal, Shubham
Das, Prasanta Kumar
and
Dhar, Purbarun
2023.
Wavy Marangoni effect and strategic slip-pattern-driven species transport in micro-confined sandwiched liquid films.
Journal of Fluid Mechanics,
Vol. 976,
Issue. ,
HU, Penghui
and
HU, Kaixin
2023.
Instability of Viscoelastic Thermocapillary Liquid Layers with Two Free Surfaces.
Chinese Journal of Space Science,
Vol. 43,
Issue. 4,
p.
1.
Chen, Enhui
and
Xu, Feng
2023.
Thermocapillary convective flow induced by a ramp heating wall.
International Journal of Heat and Mass Transfer,
Vol. 217,
Issue. ,
p.
124689.
Moatimid, Galal M.
Amer, Mohamed F. E.
and
Gad, Nada S.
2024.
The effects of energy transfer and Hall currents on the instability of a viscous liquid sheet saturated in porous medium.
Waves in Random and Complex Media,
p.
1.
Dixit, Ganesh
Bukhari, Syed Furqan
and
Patne, Ramkarn
2024.
Linear dynamics of a thick liquid layer subjected to an oblique temperature gradient.
Journal of Fluid Mechanics,
Vol. 987,
Issue. ,
Miksis, Michael J.
Neitzel, G. Paul
and
Voorhees, Peter W.
2024.
Interfacial Dynamics Pioneer Stephen H. Davis (1939–2021).
Annual Review of Fluid Mechanics,
Vol. 56,
Issue. 1,
p.
1.
Yang, Haolin
Mottram, Nigel J.
and
Kowal, Katarzyna N.
2024.
Dynamics of a thin film of fluid spreading over a lubricated substrate.
Journal of Fluid Mechanics,
Vol. 1001,
Issue. ,
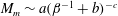 $M_{m}\sim a(\unicode[STIX]{x1D6FD}^{-1}+b)^{-c}$ for each mode, where
$M_{m}\sim a(\unicode[STIX]{x1D6FD}^{-1}+b)^{-c}$ for each mode, where 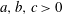 $a,b,c>0$ and
$a,b,c>0$ and  $\unicode[STIX]{x1D6FD}^{-1}$ is the slip parameter. In the limit of free slip, longitudinal travelling waves disappear in favour of longitudinal rolls. With increasing slip, it is common for two-dimensional hydrothermal waves to exchange stability in favour of longitudinal rolls and oblique hydrothermal waves. Two types of oblique hydrothermal waves appear under partial slip, which exchange stability with increasing slip. The oblique mode that is preferred under no slip persists and remains near longitudinal for small slip parameters.
$\unicode[STIX]{x1D6FD}^{-1}$ is the slip parameter. In the limit of free slip, longitudinal travelling waves disappear in favour of longitudinal rolls. With increasing slip, it is common for two-dimensional hydrothermal waves to exchange stability in favour of longitudinal rolls and oblique hydrothermal waves. Two types of oblique hydrothermal waves appear under partial slip, which exchange stability with increasing slip. The oblique mode that is preferred under no slip persists and remains near longitudinal for small slip parameters.

