Hostname: page-component-586b7cd67f-2plfb Total loading time: 0 Render date: 2024-11-23T07:39:01.491Z Has data issue: false hasContentIssue false
  • English
  • Français

The trapping and release of bubbles from a linear pore

Published online by Cambridge University Press:  28 March 2013

Geoffrey Dawson ,
Sungyon Lee  and
Anne Juel
Geoffrey Dawson
Affiliation:
Manchester Centre for Nonlinear Dynamics and School of Mathematics, University of Manchester, Manchester M13 9PL, UK
Sungyon Lee
Affiliation:
UCLA Mathematics Department, Box 951555, Los Angeles, CA 90095-1555, USA
Anne Juel*
Affiliation:
Manchester Centre for Nonlinear Dynamics and School of Mathematics, University of Manchester, Manchester M13 9PL, UK
*
†Email address for correspondence: anne.juel@manchester.ac.uk
Get access Rights & Permissions [Opens in a new window]

Abstract

Streamwise variation in vessel geometry is a feature of many multiphase flows of practical interest, ranging from natural porous media flows to man-made lab-on-the-chip applications. The variable streamwise geometry typically exerts a dominant influence on bubble motion, and can lead to undesirable phenomena such as clogging of the vessel. Here, we study clogging in a fundamental configuration, where a tube of square cross-section is suddenly expanded over a short streamwise distance. The extent to which a bubble driven by constant flux flow broadens to partially fill the expansion depends on the balance between viscous and surface tension stresses, measured by the capillary number 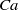$\mathit{Ca}$. This broadening is accompanied by the slowing and momentary arrest of the bubble as 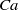$\mathit{Ca}$ is reduced towards its critical value for trapping. For 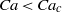$\mathit{Ca}\lt {\mathit{Ca}}_{c} $ the pressure drag forces on the quasi-arrested bubble are insufficient to force the bubble out of the expanded region so it remains trapped. We examine the conditions for trapping by varying bubble volume, flow rate of the carrier fluid, relative influence of gravity and length of expanded region. We find specifically that 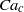${\mathit{Ca}}_{c} $ depends non-monotonically on the size of the bubble. We verify, with experiments and a capillary static model, that a bubble is released if the work of the pressure forces over the length of the trap exceeds the surface energy required for the trapped bubble to reenter the constricted square tube.

JFM classification

Interfacial Flows (free surface): Capillary flows Drops and Bubbles: Drops and Bubbles Micro-/Nano-fluid dynamics: Microfluidics
Type
Papers
Information
Journal of Fluid Mechanics , Volume 722 , 10 May 2013 , pp. 437 - 460
Copyright
©2013 Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abbyad, P., Dangla, R., Alexandrou, A. & Baroud, C. N. 2011 Rails and anchors: guiding and trapping droplet microreactors in two dimensions. Lab on a Chip 11, 813–821.CrossRefGoogle ScholarPubMed
Ahn, B., Lee, K., Lee, H., Panchapakesan, R. & Oh, K. W. 2011 Parallel synchronization of two trains of droplets using a railroad-like channel network. Lab on a Chip 11, 3956–3962.CrossRefGoogle ScholarPubMed
Amyot, O. & Plouraboué, F. 2007 Capillary pinching in a pinched microchannel. Phys. Fluids 19, 033101.CrossRefGoogle Scholar
Boukellal, H., Selimovic, S., Jia, Y., Cristobal, G. & Fraden, S. 2009 Simple, robust storage of drops and fluids in a microfluidic device. Lab on a Chip 9, 331–338.CrossRefGoogle Scholar
Brakke, K. 2008 Surface Evolver manual. http://www.susqu.edu/facstaff/b/brakke/evolver/evolver.html.Google Scholar
Chio, H., Jensen, M. J., Wang, X., Bruus, H. & Attinger, D. 2006 Transient pressure drops of gas bubbles passing through liquid-filled microchannel contractions: an experimental study. J. Micromech. Microengng 16, 143–149.CrossRefGoogle Scholar
Dangla, R., Lee, S. & Baroud, C. N. 2011 Trapping microfluidic drops in wells of surface energy. Phys. Rev. Lett. 107, 124501.CrossRefGoogle ScholarPubMed
Gu, H., Murade, C. U., Duits, M. H. G. & Mugele, F. 2011 A microfluidic platform for on-demand formation and merging of microdroplets using electric control. Biomicrofluidics 5 (1), 011101.CrossRefGoogle ScholarPubMed
Hazel, A. L. & Heil, M. 2002 The steady propagation of a semi-infinite a semi-infinite bubble into a tube of elliptical or rectangular cross-section. J. Fluid Mech. 470, 91–114.CrossRefGoogle Scholar
He, M., Kuo, J. S. & Chiu, D. T. 2005 Electro-generation of single femtoliter- and picoliter-volume aqueous droplets in microfluidic systems. Appl. Phys. Lett. 87 (3), 031916.CrossRefGoogle Scholar
Janssen, P. J. A. & Anderson, P. D. 2008 A boundary-integral model for drop deformation between two parallel plates with non-unit viscosity ratio drops. J. Comp. Phys. 227, 8807–8819.CrossRefGoogle Scholar
Jensen, M. J., Goranovi, G. & Bruus, H. 2004 The clogging pressure of bubbles in hydrophilic microchannel contractions. J. Micromech. Microengng 14, 876–883.CrossRefGoogle Scholar
Jensen, M. J., Stone, H. A. & Bruus, H. 2006 A numerical study of two-phase Stokes flow in an axisymmetric flow-focusing device. Phys. Fluids 18, 077103.CrossRefGoogle Scholar
Köhler, J. M., Henkel, T., Grodrian, A., Kirner, T., Roth, M., Martin, K. & Metze, J. 2004 Digital reaction technology by micro segmented flow-components, concepts and applications. Chem. Engng J. 101, 201–216.CrossRefGoogle Scholar
Legait, B. 1983 Laminar flow of two phases through a capillary tube with variable square cross section. J. Colloid Interface Sci. 96, 28–38.CrossRefGoogle Scholar
de Lózar, A., Heap, A., Box, F., Hazel, A. L. & Juel, A. 2009 Partially-occluded tubes can force switch-like transitions in the behaviour of propagating bubbles. Phys. Fluids 21, 101702.CrossRefGoogle Scholar
de Lózar, A., Juel, A. & Hazel, A. L. 2008 The steady propagation of an air finger into a rectangular tube. J. Fluid Mech. 614, 173–195.CrossRefGoogle Scholar
Lundström, T. S. 1996 Bubble transport through constricted capillary tubes with application to resin transfer molding. Polym. Compos. 17, 770–779.CrossRefGoogle Scholar
Pailha, M., Hazel, A. L., Glendinning, P. A. & Juel, A. 2012 Oscillatory bubbles induced by geometric constraint. Phys. Fluids 24, 021702.CrossRefGoogle Scholar
Ransohoff, T. C. & Radke, C. J. 1988 Laminar flow of a wetting liquid along the corners of a predominantly gas-occupied noncircular pore. J. Colloid Interface Sci. 121 (2), 392–401.CrossRefGoogle Scholar
Renvoisé, P., Bush, J. W. M., Prakash, M. & Quéré, D. 2009 Drop propulsion in tapered tubes. Europhys. Lett. 86, 64003.CrossRefGoogle Scholar
Tan, Y.-C., Fisher, J. S., Lee, A. I., Cristini, V. & Lee, A. P. 2004 Design of microfluidic channel geometries for the control of droplet volume, chemical concentration, and sorting. Lab on a Chip 4, 292–298.CrossRefGoogle ScholarPubMed
Um, E. & Park, J.-K. 2009 A microfluidic abacus channel for controlling the addition of droplets. Lab on a Chip 9, 207–212.CrossRefGoogle ScholarPubMed
Wong, H., Radke, C. J. & Morris, S. 1995a The motion of long bubbles in polygonal capillaries. Part 1. Thin films. J. Fluid Mech. 292, 71–94.CrossRefGoogle Scholar
Wong, H., Radke, C. J. & Morris, S. 1995b The motion of long bubbles in polygonal capillaries. Part 2. Drag, fluid pressure and fluid flow. J. Fluid Mech. 292, 95–110.CrossRefGoogle Scholar
Xu, J. & Attinger, D. 2008 Drop on demand in a microfluidic chip. J. Micromech. Microeng. 18 (6), 065020.CrossRefGoogle Scholar

Dawson et al. supplementary movie

Motion of bubble through a sudden expansion when Ca=1.1Cacrit, L/w=4.22 and w=3.0mm.

Download Dawson et al. supplementary movie(Video)
Video 147.6 KB

Dawson et al. supplementary movie

Trapping of a bubble in a sudden expansion when Ca=0.98Cacrit, L/w=4.22 and w=3.0mm.

Download Dawson et al. supplementary movie(Video)
Video 125.4 KB