Hostname: page-component-586b7cd67f-tf8b9 Total loading time: 0 Render date: 2024-11-25T03:53:05.004Z Has data issue: false hasContentIssue false
  • English
  • Français

A two-dimensional-three-component model for spanwise rotating plane Poiseuille flow

Published online by Cambridge University Press:  09 October 2019

Shengqi Zhang ,
Zhenhua Xia Open the ORCID record for Zhenhua Xia [Opens in a new window] ,
Yipeng Shi  and
Shiyi Chen
Shengqi Zhang
Affiliation:
State Key Laboratory for Turbulence and Complex Systems, Peking University, Beijing 100871, China
Zhenhua Xia*
Affiliation:
Department of Engineering Mechanics, Zhejiang University, Hangzhou 310027, China
Yipeng Shi
Affiliation:
State Key Laboratory for Turbulence and Complex Systems, Peking University, Beijing 100871, China
Shiyi Chen*
Affiliation:
State Key Laboratory for Turbulence and Complex Systems, Peking University, Beijing 100871, China Department of Engineering Mechanics, Zhejiang University, Hangzhou 310027, China Department of Mechanics and Aerospace Engineering, Southern University of Science and Technology, Shenzhen 518055, China
*
†Email addresses for correspondence: xiazh@zju.edu.cn, chensy@sustech.edu.cn
†Email addresses for correspondence: xiazh@zju.edu.cn, chensy@sustech.edu.cn
Get access Rights & Permissions [Opens in a new window]

Abstract

Spanwise rotating plane Poiseuille flow (RPPF) is one of the canonical flow problems to study the effect of system rotation on wall-bounded shear flows and has been studied a lot in the past. In the present work, a two-dimensional-three-component (2D/3C) model for RPPF is introduced and it is shown that the present model is equivalent to a thermal convection problem with unit Prandtl number. For low Reynolds number cases, the model can be used to study the stability behaviour of the roll cells. It is found that the neutral stability curves, critical eigensolutions and critical streamfunctions of RPPF at different rotation numbers ($Ro$) almost collapse with the help of a rescaling with a newly defined Rayleigh number 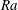$Ra$ and channel height 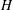$H$. Analytic expressions for the critical Reynolds number and critical wavenumber at different 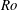$Ro$ can be obtained. For a turbulent state with high Reynolds number, the 2D/3C model for RPPF is self-sustained even without extra excitations. Simulation results also show that the profiles of mean streamwise velocity and Reynolds shear stress from the 2D/3C model share the same linear laws as the fully three-dimensional cases, although differences on the intercepts can be observed. The contours of streamwise velocity fluctuations behave like plumes in the linear law region. We also provide an explanation to the linear mean velocity profiles observed at high rotation numbers.

JFM classification

Turbulent Flows: Rotating turbulence Convection: Plumes/thermals
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 880 , 10 December 2019 , pp. 478 - 496
Copyright
© 2019 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Ahlers, G., Grossmann, S. & Lohse, D. 2009 Heat transfer and large scale dynamics in turbulent Rayleigh–Bénard convection. Rev. Mod. Phys. 81, 503–537.Google Scholar
Bobba, K. M.2004 Robust flow stability: theory, computations and experiments in near wall turbulence. PhD thesis, California Institute of Technology, Pasadena, CA.Google Scholar
Bodenschatz, E., Pesch, W. & Ahlers, G. 2000 Recent developments in Rayleigh–Bénard convection. Annu. Rev. Fluid Mech. 32, 709–778.Google Scholar
Bradshaw, P. 1969 The analogy between streamline curvature and buoyancy in turbulent shear flow. J. Fluid Mech. 36 (1), 177–191.Google Scholar
Brethouwer, G. 2016 Linear instabilities and recurring bursts of turbulence in rotating channel flow simulations. Phys. Rev. Fluids 1 (5), 054404.Google Scholar
Brethouwer, G. 2017 Statistics and structure of spanwise rotating turbulent channel flow at moderate Reynolds numbers. J. Fluid Mech. 828, 424–458.Google Scholar
Brethouwer, G., Schalatter, P., Duguet, Y., Henningson, D. S. & Johansson, A. V. 2014 Recurrent bursts via linear processes in turbulent environments. Phys. Rev. Lett. 112, 144502.Google Scholar
Dai, Y. J., Huang, W. X. & Xu, C. X. 2016 Effects of Taylor–Görtler vortices on turbulent flows in a spanwise-rotating channel. Phys. Fluids 28, 115104.Google Scholar
Farrell, B. F. & Ioannou, P. J. 2017 Statistical state dynamics-based analysis of the physical mechanisms sustaining and regulating turbulence in Couette flow. Phys. Rev. Fluids 2 (8), 084608.Google Scholar
Farrell, B. F., Ioannou, P. J., Jiménez, J., Constantinou, N. C., Lozano-Durán, A. & Nikolaidis, M.-A. 2016 A statistical state dynamics-based study of the structure and mechanism of large-scale motions in plane Poiseuille flow. J. Fluid Mech. 809, 290–315.Google Scholar
Farrell, B. F., Ioannou, P. J. & Nikolaidis, M.-A.2018 Parametric mechanism maintaining Couette flow turbulence verified in DNS implies novel control strategies. J. Fluid Mech. (submitted) arXiv:1808.03870v2.Google Scholar
Gayme, D. F., McKeon, B. J., Bamieh, B., Papachristodoulou, A. & Doyle, J. C. 2011 Amplification and nonlinear mechanisms in plane Couette flow. Phys. Fluids 23 (6), 065108.Google Scholar
Gayme, D. F., McKeon, B. J., Papachristodoulou, A., Bamieh, B. & Doyle, J. C. 2010 A streamwise constant model of turbulence in plane Couette flow. J. Fluid Mech. 665, 99–119.Google Scholar
Grundestam, O., Wallin, S. & Johansson, A. V. 2008 Direct numerical simulations of rotating turbulent channel flow. J. Fluid Mech. 598, 177–199.Google Scholar
Halleen, R. M. & Johnston, J. P.1967 The influence of rotation on flow in a long rectangular channel: an experimental study. Tech. Rep. Stanford University California Thermosciences Division.Google Scholar
Hart, J. E. 1971 Instability and secondary motion in a rotating channel flow. J. Fluid Mech. 45, 341–351.Google Scholar
Hsieh, A. & Biringen, S. 2016 The minimal flow unit in complex turbulent flows. Phys. Fluids 28 (12), 125102.Google Scholar
Jakirlić, S., Hanjalić, K. & Tropea, C. 2002 Modeling rotating and swirling turbulent flows: A perpetual challenge. AIAA J. 40, 1984–1996.Google Scholar
Johnston, J. P., Halleen, R. M. & Lezius, D. K. 1972 Effects of spanwise rotation on the structure of two-dimensional fully developed turbulent channel flow. J. Fluid Mech. 56, 533–557.Google Scholar
Kadanoff, L. P. 2001 Turbulent heat flow: structures and scaling. Phys. Today 54 (8), 34–39.Google Scholar
Kristoffersen, R. & Andersson, H. I. 1993 Direct simulations of low-Reynolds-number turbulent flow in a rotating channel. J. Fluid Mech. 256, 163–197.Google Scholar
Lezius, D. K. & Johnston, J. P. 1976 Roll-cell instabilities in rotating laminar and trubulent channel flows. J. Fluid Mech. 77, 153–174.Google Scholar
Lohse, D. & Xia, K. Q. 2010 Small-scale properties of turbulent Rayleigh–Bénard convection. Annu. Rev. Fluid Mech. 42, 335–364.Google Scholar
Maciel, Y., Picard, D., Yan, G., Dumas, G. & Gleyzes, C. 2003 Fully developed turbulent channel flow subject to system rotation. In 33rd AIAA Fluid Dynamics Conference and Exhibit, Orlando, Florida, 2003-4153.Google Scholar
Nakabayashi, K. & Kitoh, O. 1996 Low Reynolds number fully developed two-dimensional turbulent channel flow with system rotation. J. Fluid Mech. 315, 1–29.Google Scholar
Nakabayashi, K. & Kitoh, O. 2005 Turbulence characteristics of two-dimensional channel flow with system rotation. J. Fluid Mech. 528, 355–377.Google Scholar
Palm, E. 1975 Nonlinear thermal convection. Annu. Rev. Fluid Mech. 7, 39–61.Google Scholar
Speziale, C. G. & Thangam, S. 1983 Numerical study of secondary flows and roll-cell instabilities in rotating channel flow. J. Fluid Mech. 130, 377–395.Google Scholar
Tafti, D. K. & Vanka, S. P.1990 Large eddy simulation of channel flow using finite-difference techniques. Comp. Fluid Dynamics Laboratory Report CFD, pp. 90–01.Google Scholar
Tanaka, M., Kida, S., Yanase, S. & Kawahara, G. 2000 Zero-absolute-vorticity state in a rotating turbulent shear flow. Phys. Fluids 12 (8), 1979–1985.Google Scholar
Thomas, V. L., Lieu, B. K., Jovanović, M. R., Farrell, B. F., Ioannou, P. J. & Gayme, D. F. 2014 Self-sustaining turbulence in a restricted nonlinear model of plane couette flow. Phys. Fluids 26 (10), 105112.Google Scholar
Tritton, D. J. 1992 Stabilization and destabilization of turbulent shear flow in a rotating fluid. J. Fluid Mech. 241, 503–523.Google Scholar
Wallin, S., Grundestam, O. & Johansson, A. V. 2013 Laminarization mechanisms and extreme-amplitude states in rapidly rotating plane channel flow. J. Fluid Mech. 730, 193–219.Google Scholar
Xi, H.-D., Lam, S. & Xia, K.-Q. 2004 From laminar plumes to organized flows: the onset of large-scale circulation in turbulent thermal convection. J. Fluid Mech. 503, 47–56.Google Scholar
Xia, Z. H., Shi, Y. P. & Chen, S. Y. 2016 Direct numerical simulation of turbulent channel flow with spanwise rotation. J. Fluid Mech. 788, 42–56.Google Scholar
Yang, Y. & Pullin, D. I. 2011 Geometric study of Lagrangian and eulerian structures in turbulent channel flow. J. Fluid Mech. 674, 67–92.Google Scholar
Yang, Y.-T. & Wu, J.-Z. 2012 Channel turbulence with spanwise rotation studied using helical wave decomposition. J. Fluid Mech. 692, 137–152.Google Scholar

Zhang et al. supplementary movie 1

Contours of u′ from Case 2D_Ro1

Download Zhang et al. supplementary movie 1(Video)
Video 9.1 MB

Zhang et al. supplementary movie 2

Contours of u′ from Case 2D_Ro40

Download Zhang et al. supplementary movie 2(Video)
Video 11.1 MB