Hostname: page-component-586b7cd67f-2brh9 Total loading time: 0 Render date: 2024-11-25T04:40:38.476Z Has data issue: false hasContentIssue false
  • English
  • Français

Understanding evolution of vortex rings in viscous fluids

Published online by Cambridge University Press:  13 December 2017

Aashay Tinaikar Open the ORCID record for Aashay Tinaikar [Opens in a new window] ,
S. Advaith  and
S. Basu Open the ORCID record for S. Basu [Opens in a new window]
Aashay Tinaikar*
Affiliation:
Interdisciplinary Centre for Energy Research, Indian Institute of Science, Bangalore-560012, Karnataka, India
S. Advaith
Affiliation:
Interdisciplinary Centre for Energy Research, Indian Institute of Science, Bangalore-560012, Karnataka, India
S. Basu
Affiliation:
Interdisciplinary Centre for Energy Research, Indian Institute of Science, Bangalore-560012, Karnataka, India Department of Mechanical Engineering, Indian Institute of Science, Bangalore-560012, Karnataka, India
*
†Email address for correspondence: tinaikar.aashay@gmail.com
Get access Rights & Permissions [Opens in a new window]

Abstract

The evolution of vortex rings in isodensity and isoviscosity fluid has been studied analytically using a novel mathematical model. The model predicts the spatiotemporal variation in peak vorticity, circulation, vortex size and spacing based on instantaneous vortex parameters. This proposed model is quantitatively verified using experimental measurements. Experiments are conducted using high-speed particle image velocimetry (PIV) and laser induced fluorescence (LIF) techniques. Non-buoyant vortex rings are generated from a nozzle using a constant hydrostatic pressure tank. The vortex Reynolds number based on circulation 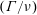$(\unicode[STIX]{x1D6E4}/\unicode[STIX]{x1D708})$ is varied in the range 100–1500 to account for a large range of operating conditions. Experimental results show good agreement with theoretical predictions. However, it is observed that neither Saffman’s thin-core model nor the thick-core equations could correctly explain vortex evolution for all initial conditions. Therefore, a transitional theory is framed using force balance equations which seamlessly integrate short- and long-time asymptotic theories. It is found that the parameter 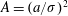$A=(a/\unicode[STIX]{x1D70E})^{2}$, where $a$ is the vortex half-spacing and $\unicode[STIX]{x1D70E}$ denotes the standard deviation of the Gaussian vorticity profile, governs the regime of vortex evolution. For higher values of 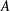$A$, evolution follows short-time behaviour, while for 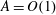$A=O(1)$, long-time behaviour is prominent. Using this theory, many reported anomalous observations have been explained.

JFM classification

Vortex Flows: Vortex dynamics Vortex Flows: Vortex Flows Wakes/Jets: Vortex streets
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 836 , 10 February 2018 , pp. 873 - 909
Check for updates
Copyright
© 2017 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Advaith, S., Manu, K. V., Tinaikar, A., Chetia, U. K. & Basu, S. 2017 Interaction of vortex ring with a stratified finite thickness interface. Phys. Fluids 29 (9), 093602.Google Scholar
Archer, P. J., Thomas, T. G. & Coleman, G. N. 2008 Direct numerical simulation of vortex ring evolution from the laminar to the early turbulent regime. J. Fluid Mech. 598, 201–226.Google Scholar
Arvidsson, P. M., Kovács, S. J., Töger, J., Borgquist, R., Heiberg, E., Carlsson, M. & Arheden, H. 2016 Vortex ring behavior provides the epigenetic blueprint for the human heart. Sci. Rep. 6, 22021.Google Scholar
Auerbach, D. 1988 Some open questions on the flow of circular vortex rings. Fluid Dyn. Res. 3 (1–4), 209–213.Google Scholar
Barenblatt, G. I. 1996 Scaling, Self-similarity, and Intermediate Asymptotics: Dimensional Analysis and Intermediate Asymptotics, vol. 14. Cambridge University Press.Google Scholar
Batchelor, G. K. 2000 An Introduction to Fluid Dynamics. Cambridge University Press.CrossRefGoogle Scholar
Bergdorf, M., Koumoutsakos, P. & Leonard, A. 2007 Direct numerical simulations of vortex rings at Re gamma = 7500. J. Fluid Mech. 581, 495–505.Google Scholar
Bond, D. & Johari, H. 2010 Impact of buoyancy on vortex ring development in the near field. Exp. Fluids 48 (5), 737–745.Google Scholar
Cantwell, B. & Rott, N. 1988 The decay of a viscous vortex pair. Phys. Fluids 31 (11), 3213–3224.Google Scholar
Cater, J., Soria, J. & Lim, T. T. 1998 The vorticity of a vortex ring core. In Proceedings of the 13th Australasian Fluid Mechanics Conference, Melbourne, Australia, pp. 5–8. Monash University Publishing.Google Scholar
Dabiri, J. O. 2009 Optimal vortex formation as a unifying principle in biological propulsion. Annu. Rev. Fluid Mech. 41, 17–33.Google Scholar
Dabiri, J. O. & Gharib, M. 2005 The role of optimal vortex formation in biological fluid transport. Proc. R. Soc. Lond. B 272 (1572), 1557–1560.Google Scholar
Dahm, W. J. A., Scheil, C. M. & Tryggvason, G. 1989 Dynamics of vortex interaction with a density interface. J. Fluid Mech. 205, 1–43.Google Scholar
Dengler, K. & Reeder, M. J. 1997 The effects of convection and baroclinicity on the motion of tropical-cyclone-like vortices. Q. J. R. Meteorol. Soc. 123 (539), 699–725.Google Scholar
Didden, N. 1979 On the formation of vortex rings: rolling-up and production of circulation. Z. Angew. Math. Phys. 30 (1), 101–116.Google Scholar
Dyson, F. W. 1893 The potential of an anchor ring. Part II. Phil. Trans. R. Soc. Lond. A 184, 1041–1106.Google Scholar
Dziedzic, M. & Leutheusser, H. J. 1996 An experimental study of viscous vortex rings. Exp. Fluids 21 (5), 315–324.Google Scholar
Emanuel, K. 2005 Increasing destructiveness of tropical cyclones over the past 30 years. Nature 436 (7051), 686–688.Google Scholar
Fohl, T. 1967 Optimization of flow for forcing stack wastes to high altitudes. J. Air Pollut. Control Assoc. 17 (11), 730–733.Google Scholar
Fraenkel, L. E. 1972 Examples of steady vortex rings of small cross-section in an ideal fluid. J. Fluid Mech. 51 (01), 119–135.Google Scholar
Fukumoto, Y. & Kaplanski, F. 2008 Global time evolution of an axisymmetric vortex ring at low Reynolds numbers. Phys. Fluids 20 (5), 053103.CrossRefGoogle Scholar
Fukumoto, Y. & Moffatt, H. K. 2000 Motion and expansion of a viscous vortex ring. Part 1. A higher-order asymptotic formula for the velocity. J. Fluid Mech. 417, 1–45.Google Scholar
Gharib, M., Rambod, E., Kheradvar, A., Sahn, D. J. & Dabiri, J. O. 2006 Optimal vortex formation as an index of cardiac health. Proc. Natl Acad. Sci. USA 103 (16), 6305–6308.Google Scholar
Gharib, M., Rambod, E. & Shariff, K. 1998 A universal time scale for vortex ring formation. J. Fluid Mech. 360, 121–140.Google Scholar
Helmholtz, H. 1858 About integrals of hydrodynamic equations related with vortical motions. J. Reine Angew. Math. 55, 25.Google Scholar
Hill, F. M. 1975 A numerical study of the descent of a vortex pair in a stably stratified atmosphere. J. Fluid Mech. 71, 1–13.Google Scholar
Hill, M. J. M. 1894 On a spherical vortex. Proc. R. Soc. Lond. A 55 (331–335), 219–224.Google Scholar
Jacquin, L., Fabre, D., Sipp, D., Theofilis, V. & Vollmers, H. 2003 Instability and unsteadiness of aircraft wake vortices. Aerosp. Sci. Technol. 7 (8), 577–593.Google Scholar
Johari, H. & Fang, H. 1997 Horizontal vortex ring motion in linearly stratified media. Phys. Fluids 9 (9), 2605–2616.Google Scholar
Keane, R. D. & Adrian, R. J. 1990 Optimization of particle image velocimeters. I. Double pulsed systems. Meas. Sci. Technol. 1 (11), 1202.Google Scholar
Kelvin, L. 1867 On vortex atoms. Proc. R. Soc. Edin. 6, 94–105.Google Scholar
Lamb, H. 1932 Hydrodynamics. Cambridge University Press.Google Scholar
Lee, J. S., Park, S. J., Lee, J. H., Weon, B. M., Fezzaa, K. & Je, J. H. 2015 Origin and dynamics of vortex rings in drop splashing. Nature Commun. 6.CrossRefGoogle ScholarPubMed
Linden, P. F. 1973 The interaction of a vortex ring with a sharp density interface: a model for turbulent entrainment. J. Fluid Mech. 60, 467–480.Google Scholar
Lugt, H. J. 1983 Vortex Flow in Nature and Technology, vol. 1. p. 305. Wiley-Interscience.Google Scholar
Manu, K. V., Anand, P., Chetia, U. K. & Basu, S. 2015 Effects of instabilities and coherent structures on the performance of a thermocline based thermal energy storage. Appl. Therm. Engng 87, 768–778.Google Scholar
Maxworthy, T. 1972 The structure and stability of vortex rings. J. Fluid Mech. 51 (01), 15–32.Google Scholar
Maxworthy, T. 1977 Some experimental studies of vortex rings. J. Fluid Mech. 81 (03), 465–495.Google Scholar
Moore, D. W. & Saffman, P. G. 1973 Axial flow in laminar trailing vortices. Proc. R. Soc. Lond. A 333, 491–508.Google Scholar
Nomura, K. K., Tsutsui, H., Mahoney, D. & Rottman, J. W. 2006 Short-wavelength instability and decay of a vortex pair in a stratified fluid. J. Fluid Mech. 553, 283–322.Google Scholar
Orlandi, P., Egermann, P. & Hopfinger, E. J. 1998 Vortex rings descending in a stratified fluid. Phys. Fluids 10 (11), 2819–2827.Google Scholar
Oseen, C. W. 1910 Stokes’ formula and a related theorem in hydrodynamics. Ark. Mat. Astron. Fys. 6, 20.Google Scholar
Oshima, Y. 1972 Motion of vortex rings in water. J. Phys. Soc. Japan 32 (4), 1125–1131.Google Scholar
Pullin, D. I. 1979 Vortex ring formation at tube and orifice openings. Phys. Fluids 22 (3), 401–403.Google Scholar
Pullin, D. I. & Saffman, P. G. 1998 Vortex dynamics in turbulence. Annu. Rev. Fluid Mech. 30 (1), 31–51.Google Scholar
Raffel, M., Willert, C. E., Wereley, S. & Kompenhans, J. 2013 Particle Image Velocimetry: A Practical Guide. Springer.Google Scholar
Rayfield, G. W. & Reif, F. 1964 Quantized vortex rings in superfluid helium. Phys. Rev. 136, A1194–A1208.Google Scholar
Reynolds, O. 1876 On the resistance encountered by vortex rings and the relation between vortex rings and the stream-lines of a disc. Nature 14, 477–479.Google Scholar
Saffman, P. G. 1970 The velocity of viscous vortex rings. Stud. Appl. Maths 49 (4), 371–380.Google Scholar
Saffman, P. G. 1978 The number of waves on unstable vortex rings. J. Fluid Mech. 84 (04), 625–639.Google Scholar
She, Z.-S., Jackson, E. & Orszag, S. A. 1990 Intermittant vortex structures in homogeneous isotropic turbulence. Nature 344 (6263), 226.Google Scholar
Smith, R. K., Montgomery, M. T. & Zhu, H. 2005 Buoyancy in tropical cyclones and other rapidly rotating atmospheric vortices. Dyn. Atmos. Oceans 40 (3), 189–208.Google Scholar
Sommerfeld, A. 1950 Lectures on Theoretical Physics, Vol. II: Mechanics of Deformable Bodies. Academic.Google Scholar
Sonin, E. B. 2016 Dynamics of Quantised Vortices in Superfluids. Cambridge University Press.Google Scholar
Spalart, P. R. 1998 Airplane trailing vortices. Annu. Rev. Fluid Mech. 30, 107–138.Google Scholar
Spedding, G. R., Hedenström, A. & Rosén, M. 2003 Quantitative studies of the wakes of freely flying birds in a low-turbulence wind tunnel. Exp. Fluids 34 (2), 291–303.Google Scholar
Stanaway, S. K., Cantwell, B. J. & Spalart, P. R.1988 A numerical study of viscous vortex rings using a spectral method.Google Scholar
Sullivan, I. S., Niemela, J. J., Hershberger, R. E., Bolster, D. & Donnelly, R. J. 2008 Dynamics of thin vortex rings. J. Fluid Mech. 609, 319–347.Google Scholar
Thomson, J. J. & Newall, H. F. 1885 On the formation of vortex rings by drops falling into liquids, and some allied phenomena. Proc. R. Soc. Lond. A 39, 417–436.Google Scholar
Tsai, C.-Y. & Widnall, S. E. 1976 The stability of short waves on a straight vortex filament in a weak externally imposed strain field. J. Fluid Mech. 73 (04), 721–733.Google Scholar
Turner, J. S. 1960 A comparison between buoyant vortex rings and vortex pairs. J. Fluid Mech. 7 (03), 419–432.CrossRefGoogle Scholar
Wakelin, S. L. & Riley, N. 1997 On the formation and propagation of vortex rings and pairs of vortex rings. J. Fluid Mech. 332, 121–139.Google Scholar
Watanabe, S., Nakamichi, K., Jang, I.-S., Kazama, K., Hasegawa, S.-I. & Ishiwata, S. 1995 Generation of a vortex ring with high Reynolds number by an exploding wire in water. J. Phys. Soc. Japan 64 (10), 3748–3757.CrossRefGoogle Scholar
Weigand, A. & Gharib, M. 1997 On the evolution of laminar vortex rings. Exp. Fluids 22 (6), 447–457.Google Scholar
Weihs, D. 1973 Hydromechanics of fish schooling. Nature 241 (5387), 290–291.Google Scholar
Witelski, T. P. & Bernoff, A. J. 1998 Self-similar asymptotics for linear and nonlinear diffusion equations. Stud. Appl. Maths 100 (2), 153–193.Google Scholar
Supplementary material: File

Kurach et al supplementary material 1

Kurach et al supplementary material

Download Kurach et al supplementary material 1(File)
File 423.4 KB