Hostname: page-component-cd9895bd7-8ctnn Total loading time: 0 Render date: 2024-12-22T16:21:44.412Z Has data issue: false hasContentIssue false
  • English
  • Français

Velocity-defect laws, log law and logarithmic friction law in the convective atmospheric boundary layer

Published online by Cambridge University Press:  26 November 2019

Chenning Tong Open the ORCID record for Chenning Tong [Opens in a new window]  and
Mengjie Ding
Chenning Tong*
Affiliation:
Department of Mechanical Engineering, Clemson University, Clemson, SC 29634, USA
Mengjie Ding
Affiliation:
Department of Mechanical Engineering, Clemson University, Clemson, SC 29634, USA
*
†Email address for correspondence: ctong@clemson.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

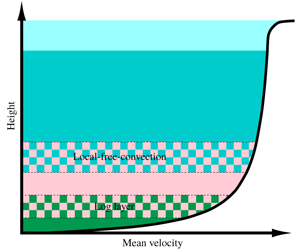
The mean velocity profile in the convective atmospheric boundary layer (CBL) is derived analytically. The shear-stress budget equations and the mean momentum equations are employed in the derivation. The multi-point Monin–Obukhov similarity (MMO) recently proposed and analytically derived by Tong & Nguyen (J. Atmos. Sci., vol. 72, 2015, pp. 4337–4348) and Tong & Ding (J. Fluid Mech., vol. 864, 2019, pp. 640–669) provides the scaling properties of the statistics in the shear-stress budget equations. Our previous and present studies have shown that the CBL is mathematically a singular perturbation problem. Therefore, we obtain the mean velocity profile using the method of matched asymptotic expansions. Three scaling layers are identified: the outer layer, which includes the mixed layer, the inner-outer layer and the inner-inner layer, which includes the roughness layer. There are two overlapping layers, the local-free-convection layer and the log layer, respectively. Two new velocity-defect laws are discovered: the mixed-layer velocity-defect law and the surface-layer velocity-defect law. The local-free-convection mean profile is obtained by asymptotically matching the expansions in the first two layers. The log law is obtained by matching the expansions in the last two layers. The von Kármán constant is obtained using velocity and length scales, and therefore has a physical interpretation. A new friction law, the convective logarithmic friction law, is obtained. The present work provides an analytical derivation of the mean velocity profile hypothesized in the Monin–Obukhov similarity theory, and is part of a comprehensive derivation of the MMO scaling from first principles.

JFM classification

Boundary Layers: Boundary layer structure Geophysical and Geological Flows: Atmospheric flows Turbulent Flows: Turbulent boundary layers
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 883 , 25 January 2020 , A36
Copyright
© 2019 Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Arya, S. P. S. 1975 Geostrophic drag and heat transfer relations for the atmospheric boundary layer. Q. J. R. Meteorol. Soc. 101, 147–161.CrossRefGoogle Scholar
Blackadar, A. K. & Tennekes, H. 1968 Asymptotic similarity in neutral barotropic planetary boundary layers. J. Atmos. Sci. 25, 1015–1020.2.0.CO;2>CrossRefGoogle Scholar
Brasseur, J. G. & Wei, T. 2010 Designing large-eddy simulation of the turbulent boundary layer to capture law-of-the-wall scaling. Phys. Fluids 22, 021303.CrossRefGoogle Scholar
Brown, R. A. 1973 On the atmospheric boundary layer: Theory and methods. Arctic Ice Dynamics Joint Experiment Bulletin 20, 1–141.Google Scholar
Businger, J. A. 1973 A note on free convection. Boundary-Layer Meteorol. 4, 323–326.CrossRefGoogle Scholar
Businger, J. A., Wyngaard, J. C., Izumi, Y. & Bradley, E. F. 1971 Flux-profile relationships in the atmospheric surface layer. J. Atmos. Sci. 28, 181–189.2.0.CO;2>CrossRefGoogle Scholar
Caughey, S. J. & Palmer, S. G. 1979 Some aspects of turbulence structure through the depth of the convective boundary layer. Q. J. R. Meteorol. Soc. 105, 811–827.CrossRefGoogle Scholar
Clarke, R. H. 1970a Observational studies in the atmospheric boundary layer. Q. J. R. Meteorol. Soc. 96, 91–114.CrossRefGoogle Scholar
Clarke, R. H. 1970b Recommended methods for the treatment of the boundary layer in numerical models. Austral. Met. Mag. 18, 51–73.Google Scholar
Clarke, R. H. 1972 Discussion of ‘observational studies in the atmospheric boundary layer’. Q. J. R. Meteorol. Soc. 98, 234–235.CrossRefGoogle Scholar
Csanady, G. T. 1967 On the resistance law of a turbulent ekman layer. J. Atmos. Sci. 24, 467–471.2.0.CO;2>CrossRefGoogle Scholar
Deardorff, J. W. 1973 An explanation of anomalously large Reynolds stresses within the convective planetary boundary layer. J. Atmos. Sci. 30, 1070–1076.2.0.CO;2>CrossRefGoogle Scholar
Garratt, J. R., Wyngaard, J. C. & Francey, R. J. 1982 Winds in the atmospheric boundary layer-prediction and observation. J. Atmos. Sci. 39, 1307–1316.2.0.CO;2>CrossRefGoogle Scholar
Grachev, A. A., Fairall, C. W. & Zilitinkevich, S. S. 1997 Surface-layer scaling for the convection induced stress regime. Boundary-Layer Meteorol. 83, 423–439.CrossRefGoogle Scholar
Kaimal, J. C. 1978 Horizontal velocity spectra in an unstable surface layer. J. Atmos. Sci. 35, 18–24.2.0.CO;2>CrossRefGoogle Scholar
Kaimal, J. C., Wyngaard, J. C., Izumi, Y. & Coté, O. R. 1972 Spectral characteristic of surface-layer turbulence. Q. J. R. Meteorol. Soc. 98, 563–589.CrossRefGoogle Scholar
von Kármán, T. 1930 Mechanische Ähnlichkeit und Turbulenz. In Proceedings of the Third International Congr. Applied Mechanics, pp. 85–105. Stockholm.Google Scholar
Kazanski, A. B. & Monin, A. S. 1960 A turbulent regime above the surface atmospheric layer. Izv. Acad. Sci., USSR, Geophys. Ser. 1, 110–112.Google Scholar
Kosović, B. 1997 Subgrid-scale modelling for the large-eddy simulation of high-Reynolds-number boundary layer. J. Fluid Mech. 336, 151–182.CrossRefGoogle Scholar
Lettau, H. H. 1959 Wind profile, surface stress and geostrophic drag coefficients in the atmospheric surface layer. Adv. Geophys. 6, 241–257.Google Scholar
Lilly, D. K. 1967 The representation of small-scale turbulence in numerical simulation experiments. In Proceedings of the IBM Scientific Computing Symp. on Environ. Sci. (ed. Goldstine, H. H.), pp. 195–210. IBM.Google Scholar
Lilly, D. K. 1968 Models of cloud-topped mixed layers under a strong inversion. Q. J. R. Meteorol. Soc. 94, 292–309.CrossRefGoogle Scholar
Lumley, J. L. & Panofsky, H. A. 1964 The Structure of Atmospheric Turbulence, Interscience Monographs and Texts in Physics and Astronomy, vol. 12. Interscience.Google Scholar
Mason, P. J. & Thomson, D. J. 1992 Stochastic backscatter in large-eddy simulations of boundary layers. J. Fluid Mech. 242, 51–78.CrossRefGoogle Scholar
Miles, N. L., Wyngaard, J. C. & Otte, M. J. 2004 Turbulent pressure statistics in the atmospheric boundary layer from large-eddy simulation. Boundary-Layer Meteorol. 113, 161–185.CrossRefGoogle Scholar
Millikan, C. B. 1938 A critical discussion of turbulent flows in channels and circular tubes. In Proceedings of the Fifth International Conference Appl. Mech. John Wiley and Sons.Google Scholar
Moeng, C.-H. 1984 A large-eddy simulation model for the study of planetary boundary-layer turbulence. J. Atmos. Sci. 41, 2052–2062.2.0.CO;2>CrossRefGoogle Scholar
Moeng, C. H. & Wyngaard, J. C. 1988 Spectral analysis of large-eddy simulations of the convective boundary layer. J. Atmos. Sci. 45, 3573–3587.2.0.CO;2>CrossRefGoogle Scholar
Monin, A. S. & Obukhov, A. M. 1954 Basic laws of turbulent mixing in the ground layer of the atmosphere. Trans. Inst. Teoret. Geofiz. Akad. Nauk SSSR 151, 163–187.Google Scholar
Obukhov, A. M. 1946 Turbulence in the atmosphere with inhomogeneous temperature. Trans. Inst. Teoret. Geofiz. Akad. Nauk SSSR 1, 95–115.Google Scholar
Otte, M. J. & Wyngaard, J. C. 2001 Stably stratified interfacial-layer turbulence from large-eddy simulation. J. Atmos. Sci. 58, 3424–3442.2.0.CO;2>CrossRefGoogle Scholar
Panofsky, H. A. & Dutton, J. 1984 Atmospheric Turbulence. Wiley-Interscience.Google Scholar
Panton, R. L. 2005 Review of wall turbulence as described by composite expansions. Appl. Mech. Rev. 58, 1–36.CrossRefGoogle Scholar
Prandtl, L. 1925 Bericht Über die Entstehung der Turbulenz. Z. Angew. Math. Mech. 5, 136–139.CrossRefGoogle Scholar
Smagorinsky, J. 1963 General circulation experiments with the primitive equations: I. The basic equations. Mon. Weath. Rev. 91, 99–164.2.3.CO;2>CrossRefGoogle Scholar
Spalart, P. R., Moser, R. D. & Rogers, M. M. 1991 Spectral methods for the Navier–Stokes equations with one infinite and 2 periodic directions. J. Comput. Phys. 96, 297–324.CrossRefGoogle Scholar
Sullivan, P. P., McWilliams, J. C. & Moeng, C.-H. 1994 A subgrid-scale model for large-eddy simulation of planetary boundary-layer flows. Boundary-Layer Meteorol. 71, 247–276.CrossRefGoogle Scholar
Sullivan, P. P., McWilliams, J. C. & Moeng, C.-H. 1996 A grid nesting method for large-eddy simulation of planetary boundary-layer flows. Boundary-Layer Meteorol. 80, 167–202.CrossRefGoogle Scholar
Sykes, R. I., Henn, D. S. & Lewellen, W. S. 1993 Surface-layer description under free-convection conditions. Q. J. R. Meteorol. Soc. 119, 409–421.CrossRefGoogle Scholar
Tong, C. & Ding, M. 2018 Monin-Obukhov similarity and local-free-convection scaling in the atmospheric boundary layer using matched asymptotic expansions. J. Atmos. Sci. 75, 3691–3701.CrossRefGoogle Scholar
Tong, C. & Ding, M. 2019 Multi-point Monin-Obukhov similarity in the convective atmospheric surface layer using matched asymptotic expansions. J. Fluid Mech. 864, 640–669.CrossRefGoogle Scholar
Tong, C. & Nguyen, K. X. 2015 Multipoint monin-obukhov similarity and its application to turbulence spectra in the convective atmospheric surface layer. J. Atmos. Sci. 72, 4337–4348.CrossRefGoogle Scholar
Townsend, A. A. 1976 The Structure of Turbulent Shear Flows. Cambridge University Press.Google Scholar
Wyngaard, J. C. 2010 Turbulence in the Atmosphere. Cambridge University Press.CrossRefGoogle Scholar
Wyngaard, J. C. & Coté, O. R. 1971 The budgets of turbulent kinetic energy and temperature variance in the atmospheric surface layer. J. Atmos. Sci. 28, 190–201.2.0.CO;2>CrossRefGoogle Scholar
Wyngaard, J. C., Coté, O. R. & Izumi, Y. 1971 Local free convection, similarity, and the budgets of shear stress and heat flux. J. Atmos. Sci. 28, 1171–1182.2.0.CO;2>CrossRefGoogle Scholar
Zilitinkevich, S. S. 1969 On the computation of the basic parameters of the interaction between the atmosphere and the ocean. Tellus 21, 17–24.CrossRefGoogle Scholar
Zilitinkevich, S. S. 1975 Resistance laws and prediction equations for the depth of the planetary boundary layer. J. Atmos. Sci. 32, 741–752.2.0.CO;2>CrossRefGoogle Scholar
Zilitinkevich, S. S. & Chalikov, D. V. 1968 The laws of resistance and of heat and moisture exchange in the interaction between the atmosphere and an underlying surface. Izv. Atmos. and Ocean Phys. 4, 438–441.Google Scholar
Zilitinkevich, S. S. & Deardorff, J. W. 1974 Similarity theory for the planetary boundary layer of time-dependent height. J. Atmos. Sci. 31, 1449–1452.2.0.CO;2>CrossRefGoogle Scholar
Zilitinkevich, S. S., Fedorovich, E. E. & Shabalova, M. V. 1992 Numerical model of a non-steady atmospheric planetary boundary layer, based on similarity theory. Boundary-Layer Meteorol. 59, 387–411.CrossRefGoogle Scholar
Zilitinkevich, S. S., Hunt, J. C. R., Esau, I. N., Grachev, A. A., Lalas, D. P., Akylas, E., Tombrou, M., Fairall, C. W., Fernando, H. J. S., Baklanov, A. A. et al. 2006 The influence of large convective eddies on the surface-layer turbulence. Q. J. R. Meteorol. Soc. 132, 1423–1456.CrossRefGoogle Scholar
Zilitinkevich, S. S., Laikhtman, D. L. & Monin, A. S. 1967 Dynamics of the atmospheric boundary layer. Izv. Atmohs. and Ocean Phys. 3, 170–191.Google Scholar