Hostname: page-component-78c5997874-94fs2 Total loading time: 0 Render date: 2024-11-07T01:42:35.821Z Has data issue: false hasContentIssue false
  • English
  • Français

Ventilated supercavitation around a moving body in a still fluid: observation and drag measurement

Published online by Cambridge University Press:  06 September 2018

Jaeho Chung  and
Yeunwoo Cho Open the ORCID record for Yeunwoo Cho [Opens in a new window]
Jaeho Chung
Affiliation:
Department of Mechanical Engineering, Korea Advanced Institute of Science and Technology, Yuseonggu, Daejeon, 34141, Republic of Korea
Yeunwoo Cho*
Affiliation:
Department of Mechanical Engineering, Korea Advanced Institute of Science and Technology, Yuseonggu, Daejeon, 34141, Republic of Korea
*
†Email address for correspondence: ywoocho@kaist.ac.kr
Get access Rights & Permissions [Opens in a new window]

Abstract

This experimental study examines ventilated supercavity formation in a free-surface bounded environment where a body is in motion and the fluid is at rest. For a given torpedo-shaped body and water depth (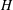$H$), depending on the cavitator diameter (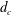$d_{c}$) and the submergence depth (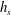$h_{s}$), four different cases are investigated according to the blockage ratio (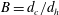$B=d_{c}/d_{h}$, where 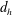$d_{h}$ is the hydraulic diameter) and the dimensionless submergence depth (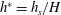$h^{\ast }=h_{s}/H$). Cases 1–4 are, respectively, no cavitator in fully submerged (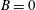$B=0$, 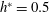$h^{\ast }=0.5$), small blockage in fully submerged (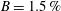$B=1.5\,\%$, 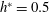$h^{\ast }=0.5$), small blockage in shallowly submerged (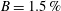$B=1.5\,\%$, 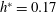$h^{\ast }=0.17$) and large blockage in fully submerged (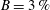$B=3\,\%$, 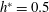$h^{\ast }=0.5$) cases. In case 1, no supercavitation is observed and only a bubbly flow (B) and a foamy cavity (FC) are observed. In non-zero blockage cases 2–4, various non-bubbly and non-foamy steady states are observed according to the cavitator-diameter-based Froude number (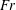$Fr$), air-entrainment coefficient (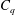$C_{q}$) and the cavitation number (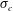$\unicode[STIX]{x1D70E}_{c}$). 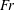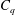The ranges of $Fr$, $C_{q}$ and 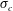$\unicode[STIX]{x1D70E}_{c}$ are $Fr=2.6{-}18.2$, 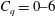$C_{q}=0{-}6$, 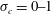$\unicode[STIX]{x1D70E}_{c}=0{-}1$ for cases 2 and 3, and 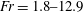$Fr=1.8{-}12.9$, 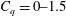$C_{q}=0{-}1.5$, 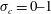$\unicode[STIX]{x1D70E}_{c}=0{-}1$ for case 4. In cases 2 and 3, a twin-vortex supercavity (TV), a reentrant-jet supercavity (RJ), a half-supercavity with foamy cavity downstream (HSF), B and FC are observed. Supercavities in case 3 are not top–bottom symmetric. In case 4, a half-supercavity with a ring-type vortex shedding downstream (HSV), double-layer supercavities (RJ inside and TV outside (RJTV), TV inside and TV outside (TVTV), RJ inside and RJ outside (RJRJ)), B, FC and TV are observed. The cavitation numbers (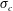$\unicode[STIX]{x1D70E}_{c}$) are approximately 0.9 for the B, FC and HSF, 0.25 for the HSV, and 0.1 for the TV, RJ, RJTV, TVTV and RJRJ supercavities. In cases 2–4, for a given 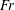$Fr$, there exists a minimum cavitation number in the formation of a supercavity while the minimum cavitation number decreases as the 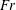$Fr$ increases. In cases 2 and 3, it is observed that a high 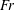$Fr$ favours an RJ and a low 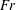$Fr$ favours a TV. For the RJ supercavities in cases 2 and 3, the cavity width is always larger than the cavity height. In addition, the cavity length, height and width all increase (decrease) as the 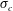$\unicode[STIX]{x1D70E}_{c}$ decreases (increases). The cavity length in case 3 is smaller than that in case 2. In both cases 2 and 3, the cavity length depends little on the 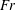$Fr$. In case 2, the cavity height and width increase as the 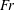$Fr$ increases. In case 3, the cavity height and width show a weak dependence on the 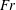$Fr$. 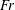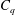Compared to case 2, for the same $Fr$, $C_{q}$ and 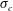$\unicode[STIX]{x1D70E}_{c}$, case 4 admits a double-layer supercavity instead of a single-layer supercavity. Connected with this behavioural observation, the body-frontal-area-based drag coefficient for a moving torpedo-shaped body with a supercavity is measured to be approximately 0.11 while that for a cavitator-free moving body without a supercavity is approximately 0.4.

JFM classification

Drops and Bubbles: Cavitation Drops and Bubbles: Drops and Bubbles
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 854 , 10 November 2018 , pp. 367 - 419
Check for updates
Copyright
© 2018 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Cameron, P. J. K., Rogers, P. H., Doane, J. W. & Gifford, D. H. 2011 An experiment for the study of free-flying supercavitating projectiles. Trans. ASME J. Fluids Engng 133 (2), 021305.Google Scholar
Campbell, I. J. & Hilborne, D. V. 1958 Air entrainment behind artificially inflated cavities. In Proc. of 2nd Symp. on Naval Hydrodynamics, Washington, DC. Office of Naval Research.Google Scholar
Ceccio, S. L. 2010 Friction drag reduction of external flows with bubble and gas injection. Annu. Rev. Fluid Mech. 42, 183–203.Google Scholar
Cox, R. N. & Clayden, W. A. 1956 Air entrainment at the rear of a steady cavity. In Proc. of Symp. on Cavitation in Hydrodynamics, London. National Physical Laboratory.Google Scholar
Epshtein, L. A. 1973 Characteristics of ventilated cavities and some scale effects, unsteady water flow with high velocities. In Proc. of IUTAM Symp. on Non-steady Flow of Water at High Speeds, Leningrad. Nauka Publishing House.Google Scholar
Franc, J. P. & Michel, J. M. 2004 Fundamentals of Cavitation. Kluwer Academic Publishers.Google Scholar
Gadd, G. E. & Grant, S. 1965 Some experiments on cavities behind disks. J. Fluid Mech. 23 (4), 645–656.Google Scholar
Garabedian, P. R. 1955 Calculation of axially symmetric cavities and jets. Pac. J. Maths. 6 (4), 611–684.Google Scholar
Goldstein, S. 1938 Modern Developments in Fluid Dynamics. Oxford University Press.Google Scholar
Haaland, S. E. 1983 Simple and explicit formulas for the friction factor in turbulent pipe flow. Trans. ASME J. Fluids Engng 105 (1), 89–90.Google Scholar
Haipeng, W., Song, F., Qin, W., Biao, H. & Guoyu, W. 2014 Experimental and numerical research on cavitating flows around axisymmetric bodies. J. Mech. Sci. 28 (11), 4527–4537.Google Scholar
Hrubes, J. D. 2001 High-speed imaging of supercavitating underwater projectiles. Exp. Fluids 30 (1), 57–64.Google Scholar
Kapankin, Y. N. & Gusev, A. V. 1984 Experimental research of joint influence of fluid and lift power of cavitator on character of flow in cavity rear part and gas departure from it. In Proc. CAHI, vol. 2244, pp. 19–28.Google Scholar
Karlikov, V. P., Reznichenko, N. T., Khomyakov, A. N. & Sholomovich, G. I. 1987 A possible mechanism for the emergence of auto-oscillations in developed artificial cavitation flows and immersed gas jets. Fluid Dyn. 22 (3), 392–398.Google Scholar
Karn, A., Arndt, R. E. A. & Hong, J. 2016 An experimental investigation into supercavity closure mechanisms. J. Fluid Mech. 789, 259–284.Google Scholar
Kawakami, E.2010 Investigation of the behavior of ventilated supercavities. MS thesis, University of Minnesota, Twin Cities.Google Scholar
Kawakami, E. & Arndt, R. E. A. 2011 Investigation of the behavior of ventilated supercavities. Trans. ASME J. Fluids Engng 133 (9), 091305.Google Scholar
Kuklinski, R., Henoch, C. & Castano, J. 2001 Experimental study of ventilated cavities on dynamic test model. In CAV2001: Fourth Intl Symp. on Cavitation, pp. 1–8. Naval Undersea Warfare Center.Google Scholar
Logvinovich, G. V. 1972 Hydrodynamics of Free-boundary Flows (Translated form Russian). IPST Press.Google Scholar
Nouri, N. M., Madoliat, R., Jahangardy, Y. & Abdolahi, M. 2015 A study on the effects of fluctuations of the supercavity parameters. Exp. Therm. Fluid Sci. 60, 188–200.Google Scholar
Panton, R. L. 2005 Incompressible Flow, 3rd edn. Wiley.Google Scholar
Reichardt, H.1946 The laws of cavitation bubbles at axially symmetrical bodies in a flow. Rep. and Trans. 35. Ministry of Aircraft Production, Great Britain.Google Scholar
Schaffar, M., Rey, C. & Boeglen, G. 2005 Behavior of supercavitating projectiles fired horizontally in water tank: theory and Experiments-CFD Computations with the OTi-Hull hydrocode. In Proc. Thirty fifth AIAA Fluid Dynamic Conf. and Exhi., Toronto, pp. 1–8.Google Scholar
Schauer, T. J.2003 An experimental study of a ventilated supercavitating vehicle. MS thesis, University of Minnesota, Twin Cities.Google Scholar
Self, M. W. & Ripken, J. F.1955 Steady-state cavity studies in a free-jet water tunnel. Rep. 47. St. Anthony Fall Hydraulic Laboratory, University of Minnesota, Twin Cities.Google Scholar
Semenenko, V. N. 2001a Artificial Supercavitation: Physics and Calculation. Institute of Hydromechanics, National Academy of Sciences of Ukraine.Google Scholar
Semenenko, V. N. 2001b Dynamic Processes of Supercavitation and Computer Simulation. Institute of Hydromechanics, National Academy of Sciences of Ukraine.Google Scholar
Silberman, E. & Song, C. S. 1961 Instability of ventilated cavities. J. Ship Res. 5 (1), 13–33.Google Scholar
Skidmore, G.2013 The pulsation of ventilated supercavities. Master of Science thesis, Department of Aerospace Engineering, Pennsylvania State University, University Park.Google Scholar
Song, C. S.1961 Pulsation of ventilated cavities. Rep. 32B. St. Anthony Fall Hydraulic Laboratory, University of Minnesota, Twin Cities.Google Scholar
Spurk, J. H. & König, B. 2002 On the gas loss from ventilated supercavities. Acta Mech. 155, 125–135.Google Scholar
Sumer, B. M. & Fredsoe, J 2010 Hydrodynamics Around Cylindrical Structures. World Scientific.Google Scholar
Waid, R. L.1957 Cavity shapes for circular disks at angles of attack. Rep. E-73.4. Hydrodynamics Laboratory, California Institute of Technology, Pasadena.Google Scholar
White, F. M. 1999 Fluid Mechanics, 4th edn. McGraw-Hill.Google Scholar
Zhou, J., Yu, K., Min, J. & Yang, M. 2010 The comparative study of ventilated super cavity shape in water tunnel and infinite flow field. J. Hydrodyn. B 22 (5), 689–696.Google Scholar