Hostname: page-component-669899f699-7tmb6 Total loading time: 0 Render date: 2025-04-25T14:38:19.367Z Has data issue: false hasContentIssue false
  • English
  • Français

Wave field and zonal flow of a librating disk

Published online by Cambridge University Press:  06 October 2015

Stéphane Le Dizès
Stéphane Le Dizès*
Affiliation:
CNRS, Aix Marseille Université, Centrale Marseille, IRPHE, UMR 7342, 13384 Marseille, France
*
†Email address for correspondence: ledizes@irphe.univ-mrs.fr
Get access Rights & Permissions [Opens in a new window]

Abstract

In this work, we provide a viscous solution of the wave field generated by librating a disk (harmonic oscillation of the rotation rate) in a stably stratified rotating fluid. The zonal flow (mean flow correction) generated by the nonlinear interaction of the wave field is also calculated in the weakly nonlinear framework. We focus on the low dissipative limit relevant for geophysical applications and for which the wave field and the zonal flow exhibit generic features (Ekman scaling, universal structures, etc.). General expressions are obtained which depend on the disk radius 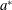$a^{\ast }$, the libration frequency 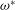${\it\omega}^{\ast }$, the rotation rate 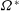${\it\Omega}^{\ast }$ of the frame, the buoyancy frequency 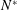$N^{\ast }$ of the fluid, its kinematic diffusion 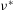${\it\nu}^{\ast }$ and its thermal diffusivity 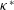${\it\kappa}^{\ast }$. When the libration frequency is in the inertia-gravity frequency interval (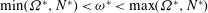$\min ({\it\Omega}^{\ast },N^{\ast })<{\it\omega}^{\ast }<\max ({\it\Omega}^{\ast },N^{\ast })$), the presence of conical internal shear layers is observed in which the spatial structures of the harmonic response and of the mean flow correction are provided. At the point of focus of these internal shear layers on the rotation axis, the largest amplitudes are obtained: the angular velocity of the harmonic response and the mean flow correction are found to be 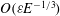$O({\it\varepsilon}E^{-1/3})$ and 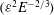$({\it\varepsilon}^{2}E^{-2/3})$ respectively, where ${\it\varepsilon}$ is the libration amplitude and 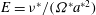$E={\it\nu}^{\ast }/({\it\Omega}^{\ast }a^{\ast 2})$ is the Ekman number. We show that the solution in the internal shear layers and in the focus region is at leading order the same as that generated by an oscillating source of axial flow localized at the edge of the disk (oscillating Dirac ring source).

JFM classification

Geophysical and Geological Flows: Rotating flows Geophysical and Geological Flows: Stratified flows Geophysical and Geological Flows: Waves in rotating fluids
Type
Papers
Information
Journal of Fluid Mechanics , Volume 782 , 10 November 2015 , pp. 178 - 208
Check for updates
Copyright
© 2015 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Abramowitz, M. & Stegun, I. A. 1965 Handbook of Mathematical Functions. Dover.Google Scholar
Aldridge, K. D. & Toomre, A. 1969 Axisymmetric inertial oscillations of a fluid in a rotating spherical container. J. Fluid Mech. 37, 307–323.Google Scholar
Barcilon, V. & Pedlosky, J. 1967 Linear theory of rotating stratified fluid motions. J. Fluid Mech. 29, 1–16.CrossRefGoogle Scholar
Bardakov, R. N., Vasil’ev, A. Y. & Chashechkin, Y. D. 2007 Calculation and measurement of conical beams of three-dimensional periodic internal waves excited by a vertically oscillating piston. Fluid Dyn. 42, 612–626.Google Scholar
Busse, F. 1968 Steady fluid flow in a precessing spheroidal shell. J. Fluid Mech. 33, 739–751.Google Scholar
Busse, F. H. 2010 Mean zonal flows generated by librations of a rotating spherical cavity. J. Fluid Mech. 650, 505–512.CrossRefGoogle Scholar
Calkins, M. A., Noir, J., Eldredge, J. D. & Aurnou, J. M. 2010 Axisymmetric simulations of libration-driven fluid dynamics in a spherical shell geometry. Phys. Fluids 22, 086602.CrossRefGoogle Scholar
Comstock, R. L. & Bills, B. G. 2003 A solar system survey of forced librations in longitude. J. Geophys. Res. 108, 5100.Google Scholar
Davis, A. M. J. & Llewellyn Smith, S. G. 2010 Tangential oscillations of a circular disk in a viscous stratified fluid. J. Fluid Mech. 656, 342–359.Google Scholar
Drazin, P. G. & Reid, W. H. 1981 Hydrodynamic Stability. Cambridge University Press.Google Scholar
Favier, B., Barker, A. J., Baruteau, C. & Ogilvie, G. I. 2014 Non-linear evolution of tidally forced inertial waves in rotating fluid bodies. Mon. Not. R. Astron. Soc. 439, 845–860.Google Scholar
Friedlander, S. & Siegmann, W. L. 1982 Internal waves in a contained rotating stratified fluid. J. Fluid Mech. 114, 123–156.Google Scholar
Fritts, D. C. & Alexander, M. J. 2003 Gravity wave dynamics and effects in the middle atmosphere. Rev. Geophys. 41 (1), 1003.Google Scholar
Greenspan, H. P. 1968 The Theory of Rotating Fluids. Cambridge University Press.Google Scholar
Il’inyhk, Y. S. & Chashechkin, Y. D. 2004 Generation of periodic motions by a disk performing torsional oscillations in a viscous, continuously stratified fluid. Fluid Dyn. 39, 148–161.Google Scholar
Kerswell, R. 1995 On the internal shear layers spawned by the critical regions in oscillatory Ekman boundary layers. J. Fluid Mech. 298, 311–325.CrossRefGoogle Scholar
Koch, S., Harlander, U., Egbers, C. & Hollerbach, R. 2013 Inertial waves in a spherical shell induced by librations of the inner sphere: experimental and numerical results. Fluid Dyn. Res. 45, 035504.Google Scholar
Le Bars, M., Cébron, D. & Le Gal, P. 2015 Flows driven by libration, precession, and tides. Annu. Rev. Fluid Mech. 47, 163–193.CrossRefGoogle Scholar
Lin, Y., Noir, J. & Calkins, M. A.2014 Inertial wave and zonal flow in librating spherical shells. arXiv:1403.1702.Google Scholar
Maas, L. R. M., Benielli, D., Sommeria, J. & Lam, F.-P. A. 1997 Observation of an internal wave attractor in a confined, stably stratified fluid. Nature 388, 557–561.Google Scholar
McEwan, A. D. 1970 Inertial oscillations in a rotating fluid cylinder. J. Fluid Mech. 40, 603–640.CrossRefGoogle Scholar
Moore, D. W. & Saffman, P. G. 1969 The structure of free vertical shear layers in a rotating fluid and the motion produced by a slowly rising body. Phil. Trans. R. Soc. Lond. A 264, 597–634.Google Scholar
Morize, C., Le Bars, M., Le Gal, P. & Tilgner, A. 2010 Experimental determination of zonal winds driven by tides. Phys. Rev. Lett. 104, 214501.Google Scholar
Mowbray, D. E. & Rarity, B. S. H. 1967 A theoretical and experimental investigation of the phase configuration of internal waves of small amplitude in a density stratified liquid. J. Fluid Mech. 28, 1–16.Google Scholar
Munk, W. & Wunsch, C. 1998 Abyssal recipes ii: energetics of tidal and wind mixing. Deep-Sea Res. 45, 1977–2010.Google Scholar
Ogilvie, G. I. & Lin, D. N. C. 2004 Tidal dissipation in rotating giant planets. Astrophys. J. 610, 477–509.CrossRefGoogle Scholar
Peacock, T., Echeverri, P. & Balmforth, N. J. 2008 An experimental investigation of internal tide generation by two-dimensional topography. J. Phys. Oceanogr. 38, 235–242.Google Scholar
Rieutord, M. 1991 Linear theory of rotating fluids using spherical harmonics. Part II, time-periodic flows. Geophys. Astrophys. Fluid Dyn. 59, 185–208.Google Scholar
Rieutord, M., Georgeot, B. & Valdettaro, L. 2001 Inertial waves in a rotating spherical shell: attractors and asymptotic spectrum. J. Fluid Mech. 435, 103–144.Google Scholar
Rieutord, M. & Valdettaro, L. 1997 Inertial waves in a rotating spherical shell. J. Fluid Mech. 341, 77–99.CrossRefGoogle Scholar
Rogers, T. M. & Glatzmaier, G. A. 2005 Gravity waves in the sun. Mon. Not. R. Astron. Soc. 364, 1135–1146.CrossRefGoogle Scholar
Sauret, A., Cébron, D., Le Bars, M. & Le Dizès, S. 2012 Fluid flows in a librating cylinder. Phys. Fluids 24, 026603.Google Scholar
Sauret, A. & Le Dizès, S. 2013 Libration-induced mean flow in a spherical shell. J. Fluid Mech. 718, 181–209.Google Scholar
St Laurent, L., Stringer, S., Garrett, C. & Perrault-Joncas, D. 2003 The generation of internal tides at abrupt topography. Deep-Sea Res. I 50, 987–1003.Google Scholar
Stewartson, K. 1957 On almost rigid rotations. J. Fluid Mech. 3, 17–26.Google Scholar
Tanzosh, J. P. & Stone, H. A. 1995 Transverse motion of a disk through a rotating viscous fluid. J. Fluid Mech. 301, 295–324.Google Scholar
Thomas, N. H. & Stevenson, T. N. 1972 A similarity solution for viscous internal waves. J. Fluid Mech. 54, 495–506.Google Scholar
Tilgner, A. 1999 Driven inertial oscillations in spherical shells. Phys. Rev. E 59, 1789–1794.Google Scholar
Tilgner, A. 2000 Oscillatory shear layers in source driven flows in an unbounded rotating fluid. Phys. Fluids 12, 1101–1111.Google Scholar
Tilgner, A. 2007 Zonal wind driven by inertial modes. Phys. Rev. Lett. 99, 194501.Google Scholar
Vedensky, D. & Ungarish, M. 1994 The motion generated by a slowly rising disk in an unbounded rotating fluid for arbitrary Taylor number. J. Fluid Mech. 262, 1–26.CrossRefGoogle Scholar
Voisin, B. 2003 Limit states of internal wave beams. J. Fluid Mech. 496, 243–293.Google Scholar
Voisin, B., Ermanyuk, E. V. & Flór, J.-B. 2011 Internal wave generation by oscillation of a sphere, with application to internal tides. J. Fluid Mech. 666, 308–357.Google Scholar
Walton, I. C. 1975 Viscous shear layers in an oscillating rotating fluid. Proc. R. Soc. Lond. A 344, 101–110.Google Scholar
Wang, C. Y. 1970 Cylindrical tank of fluid oscillating about a state of steady rotation. J. Fluid Mech. 41, 581–592.Google Scholar
Watson, G. N. 1952 Theory of Bessel Functions, 2nd edn. Cambridge University Press.Google Scholar