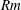Hostname: page-component-cd9895bd7-gxg78 Total loading time: 0 Render date: 2024-12-20T11:06:32.993Z Has data issue: false hasContentIssue false
  • English
  • Français

Why, how and when MHD turbulence at low $\mathit{Rm}$ becomes three-dimensional

Published online by Cambridge University Press:  18 November 2014

Alban Pothérat  and
Rico Klein
Alban Pothérat*
Affiliation:
Applied Mathematics Research Centre, Coventry University, Coventry CV5 1FB, UK
Rico Klein
Affiliation:
Technische Universität Ilmenau, Fakultät für Maschinenbau, Postfach 100565, 98684 Ilmenau, Germany
*
†Email address for correspondence: alban.potherat@coventry.ac.uk
Get access Rights & Permissions [Opens in a new window]

Abstract

Magnetohydrodynamic (MHD) turbulence at low magnetic Reynolds number is experimentally investigated by studying a liquid metal flow in a cubic domain. We focus on the mechanisms that determine whether the flow is quasi-two-dimensional, three-dimensional or in any intermediate state. To this end, forcing is applied by injecting a DC current 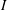$I$ through one wall of the cube only, to drive vortices spinning along the magnetic field. Depending on the intensity of the externally applied magnetic field, these vortices extend part or all of the way through the cube. Driving the flow in this way allows us to precisely control not only the forcing intensity but also its dimensionality. A comparison with the theoretical analysis of this configuration singles out the influences of the walls and of the forcing on the flow dimensionality. Flow dimensionality is characterised in several ways. First, we show that when inertia drives three-dimensionality, the velocity near the wall where current is injected scales as 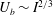$U_{b}\sim I^{2/3}$. Second, we show that when the distance 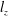$l_{z}$ over which momentum diffuses under the action of the Lorentz force (Sommeria & Moreau, J. Fluid Mech., vol. 118, 1982, pp. 507–518) reaches the channel width 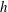$h$, the velocity near the opposite wall 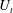$U_{t}$ follows a similar law with a correction factor 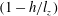$(1-h/l_{z})$ that measures three-dimensionality. When 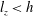$l_{z}<h$, by contrast, the opposite wall has less influence on the flow and 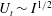$U_{t}\sim I^{1/2}$. The central role played by the ratio 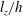$l_{z}/h$ is confirmed by experimentally verifying the scaling 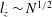$l_{z}\sim N^{1/2}$ put forward by Sommeria & Moreau (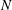$N$ is the interaction parameter) and, finally, the nature of the three-dimensionality involved is further clarified by distinguishing weak and strong three-dimensionalities previously introduced by Klein & Pothérat (Phys. Rev. Lett., vol. 104 (3), 2010, 034502). It is found that both types vanish only asymptotically in the limit 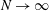$N\rightarrow \infty$. This provides evidence that because of the no-slip walls, (i) the transition between quasi-two-dimensional and three-dimensional turbulence does not result from a global instability of the flow, unlike in domains with non-dissipative boundaries (Boeck et al. Phys. Rev. Lett., vol. 101, 2008, 244501), and (ii) it does not occur simultaneously at all scales.

JFM classification

MHD and Electrohydrodynamics: MHD and Electrohydrodynamics MHD and Electrohydrodynamics: MHD turbulence
Type
Papers
Information
Journal of Fluid Mechanics , Volume 761 , 25 December 2014 , pp. 168 - 205
Check for updates
Copyright
© 2014 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Akkermans, R. A. D., Kamp, L. P. J., Clercx, H. J. H. & Van Heijst, G. H. F. 2008 Intrinsic three-dimensionality in electromagnetically driven shallow flows. Europhys. Lett. 83 (2), 24001.Google Scholar
Alboussière, T., Uspenski, V. & Moreau, R. 1999 Quasi-2D MHD turbulent shear layers. Exp. Therm. Fluid Sci. 20 (20), 19–24.CrossRefGoogle Scholar
Alpher, R. A., Hurwitz, H., Johnson, R. H. & White, D. R. 1960 Some studies of free-surface mercury magnetohydrodynamics. Rev. Mod. Phys. 4 (32), 758–774.Google Scholar
Andreev, O., Kolesnikov, Y. & Thess, A. 2013 Visualization of the Ludford column. J. Fluid Mech. 721, 438–453.Google Scholar
Boeck, T., Krasnov, D. & Thess, A. 2008 Large-scale intermittency of liquid–metal channel flow in a magnetic field. Phys. Rev. Lett. 101, 244501.Google Scholar
Davidson, P. & Pothérat, A. 2002 A note on Bodewädt–Hartmann layer. Eur. J. Mech. (B/Fluids) 21 (5), 541–559.Google Scholar
Dousset, V. & Pothérat, A 2012 Characterisation of the flow around a truncated cylinder in a duct under a spanwise magnetic field. J. Fluid Mech. 691, 341–367.CrossRefGoogle Scholar
Duran-Matute, M., Trieling, R. R. & van Heijst, G. J. F. 2010 Scaling and asymmetry in an electromagnetically forced dipolar flow structure. Phys. Rev. E 83, 016306.Google Scholar
Greenspan, H. P. 1969 Theory of Rotating Fluids. Cambridge University Press.Google Scholar
Hunt, J. C. R., Ludford, G. S. S. & Hunt, J. C. R. 1968 Three dimensional MHD duct flow with strong transverse magnetic field. Part 1. Obstacles in a constant area duct. J. Fluid Mech. 33, 693–714.Google Scholar
Kanaris, N., Albets, X., Grigoriadis, D. & Kassinos, K. 2013 3-d numerical simulations of MHD flow around a confined circular cylinder under low, moderate and strong magnetic fields. Phys. Fluids 074102.Google Scholar
Klein, R. & Pothérat, A. 2010 Appearance of three-dimensionality in wall bounded MHD flows. Phys. Rev. Lett. 104 (3), 034502.Google Scholar
Klein, R., Pothérat, A. & Alferjonok, A. 2009 Experiment on a confined electrically driven vortex pair. Phys. Rev. E 79 (1), 016304.CrossRefGoogle ScholarPubMed
Kljukin, A. & Thess, A. 1998 Direct measurement of the stream-function in a quasi-two-dimensional liquid metal flow. Exp. Fluids 25, 298–304.Google Scholar
Ludford, G. S. S. 1961 Effect of a very strong magnetic crossfield on steady motion through a slightly conducting fluid. J. Fluid Mech. 10, 141–155.CrossRefGoogle Scholar
Moreau, R. 1990 Magnetohydrodynamics. Kluwer Academic Publisher.Google Scholar
Mück, B., Günter, C. & Bühler, L. 2000 Buoyant three-dimensional MHD flows in rectangular ducts with internal obstacles. J. Fluid Mech. 418, 265–295.CrossRefGoogle Scholar
Paret, J., Marteau, D., Paireau, O. & Tabeling, P. 1997 Are flows electromagnetically forced in thin stratified layers two dimensional? Phys. Fluids 9 (10), 3102–3104.CrossRefGoogle Scholar
Pothérat, A. 2012 Three-dimensionality in quasi-two dimensional flows: recirculations and Barrel effects. Europhys. Lett. 98 (6), 64003.CrossRefGoogle Scholar
Pothérat, A. & Dymkou, V. 2010 Direct numerical simulations of low-Rm MHD turbulence based on the least dissipative modes. J. Fluid Mech. 655, 174–197.CrossRefGoogle Scholar
Pothérat, A., Rubiconi, F., Charles, Y. & Dousset, V. 2013 Direct and inverse pumping in flows with homogenenous and non-homogenous swirl. Eur. Phys. J. E 36 (8), 94.Google Scholar
Pothérat, A., Sommeria, J. & Moreau, R. 2000 An effective two-dimensional model for MHD flows with transverse magnetic field. J. Fluid Mech. 424, 75–100.Google Scholar
Pothérat, A., Sommeria, J. & Moreau, R. 2005 Numerical simulations of an effective two-dimensional model for flows with a transverse magnetic field. J. Fluid Mech. 534, 115–143.Google Scholar
Roberts, P. H. 1967 Introduction to Magnetohydrodynamics. Longmans.Google Scholar
Schumann, U. 1976 Numerical simulation of the transition from three- to two-dimensional turbulence under a uniform magnetic field. J. Fluid Mech. 35, 31–58.Google Scholar
Shats, M., Byrne, D. & Xia, H. 2010 Turbulence decay rate as a measure of flow dimensionality. Phys. Rev. Lett. 105, 264501.Google Scholar
Sommeria, J. 1986 Experimental study of the two-dimensionnal inverse energy cascade in a square box. J. Fluid Mech. 170, 139–168.Google Scholar
Sommeria, J. 1988 Electrically driven vortices in a strong magnetic field. J. Fluid Mech. 189, 553–569.Google Scholar
Sommeria, J. & Moreau, R. 1982 Why, how and when MHD turbulence becomes two-dimensional. J. Fluid Mech. 118, 507–518.Google Scholar
Sreenivasan, B. & Alboussière, T. 2002 Experimental study of a vortex in a magnetic field. J. Fluid Mech. 464, 287–309.Google Scholar
Thess, A. & Zikanov, O. 2007 Transition from two-dimensional to three-dimensional magnetohydrodynamic turbulence. J. Fluid Mech. 579, 383–412.Google Scholar
Vetcha, N., Smolentsev, S., Abdou, M. & Moreau, R. 2013 Study of instabilities and quasi-two-dimensional turbulence in volumetrically heated magnetohydrodynamic flows in a vertical rectangular duct. Phys. Fluids 25 (2), 024102.Google Scholar
Zikanov, O. & Thess, A. 1998 Direct simulation of forced MHD turbulence at low magnetic Reynolds number. J. Fluid Mech. 358, 299–333.Google Scholar