Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-29T04:07:27.038Z Has data issue: false hasContentIssue false
  • English
  • Français

Work-minimizing kinematics for small displacement of an infinitely long cylinder

Published online by Cambridge University Press:  17 April 2020

Shreyas Mandre Open the ORCID record for Shreyas Mandre [Opens in a new window]
Shreyas Mandre*
Affiliation:
Mathematics Institute, University of Warwick, CoventryCV4 7AL, UK
*
†Email address for correspondence: shreyas.mandre@warwick.ac.uk
Get access Rights & Permissions [Opens in a new window]

Abstract

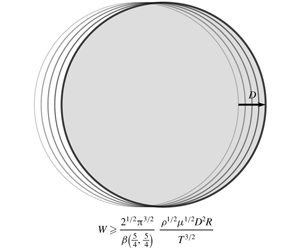
We consider the time-dependent speed of an infinitely long cylinder that minimizes the net work done on the surrounding fluid to travel a given distance perpendicular to its axis in a fixed amount of time. The flow that develops is two-dimensional. An analytical solution is possible using calculus of variations for the case that the distance travelled and the viscous boundary layer thickness that develops are much smaller than the circle radius. If $t$ represents the time since the commencement of motion and $T$ the final time, then the optimum speed profile is $Ct^{1/4}(T-t)^{1/4}$, where $C$ is determined by the distance travelled. The result also holds for rigid-body translations and rotation of cylinders formed by extrusion of smooth but otherwise arbitrary curves.

JFM classification

Mathematical Foundations: Variational methods Boundary Layers: Boundary layer control
Type
JFM Rapids
Information
Journal of Fluid Mechanics , Volume 893 , 25 June 2020 , R4
Copyright
© The Author(s), 2020. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Alben, S., Miller, L. A. & Peng, J. 2013 Efficient kinematics for jet-propelled swimming. J. Fluid Mech. 733, 100–133.CrossRefGoogle Scholar
Eloy, C. & Lauga, E. 2012 Kinematics of the most efficient cilium. Phys. Rev. Lett. 109 (3), 038101.CrossRefGoogle ScholarPubMed
Gazzola, M., Van Rees, W. M. & Koumoutsakos, P. 2012 C-start: optimal start of larval fish. J. Fluid Mech. 698, 5–18.CrossRefGoogle Scholar
Giorgio-Serchi, F. & Weymouth, G. D. 2016 Drag cancellation by added-mass pumping. J. Fluid Mech. 798, R3.CrossRefGoogle Scholar
Jones, M. & Yamaleev, N. K. 2015 Adjoint-based optimization of three-dimensional flapping-wing flows. AIAA J. 53 (4), 934–947.CrossRefGoogle Scholar
Michelin, S. & Lauga, E. 2010 Efficiency optimization and symmetry-breaking in a model of ciliary locomotion. Phys. Fluids 22 (11), 111901.CrossRefGoogle Scholar
Michelin, S. & Lauga, E. 2011 Optimal feeding is optimal swimming for all Péclet numbers. Phys. Fluids 23 (10), 101901.CrossRefGoogle Scholar
Michelin, S. & Lauga, E. 2013 Unsteady feeding and optimal strokes of model ciliates. J. Fluid Mech. 715, 1–31.CrossRefGoogle Scholar
Montenegro-Johnson, T. D. & Lauga, E. 2014 Optimal swimming of a sheet. Phys. Rev. E 89 (6), 060701(R).Google ScholarPubMed
Pesavento, U. & Wang, Z. J. 2009 Flapping wing flight can save aerodynamic power compared to steady flight. Phys. Rev. Lett. 103 (11), 118102.CrossRefGoogle ScholarPubMed
Peskin, C. S. 1982 The fluid dynamics of heart valves: Experimental, theoretical, and computational methods. Annu. Rev. Fluid Mech. 14 (1), 235–259.CrossRefGoogle Scholar
Polyanin, A. D. & Manzhirov, A. V. 1998 Handbook of Integral Equations. CRC Press.CrossRefGoogle Scholar
Quinn, D. B., Lauder, G. V. & Smits, A. J. 2015 Maximizing the efficiency of a flexible propulsor using experimental optimization. J. Fluid Mech. 767, 430–448.CrossRefGoogle Scholar
Spagnolie, S. E. & Shelley, M. J. 2009 Shape-changing bodies in fluid: Hovering, ratcheting, and bursting. Phys. Fluids 21 (1), 013103.CrossRefGoogle Scholar
Tam, D. & Hosoi, A. E. 2007 Optimal stroke patterns for Purcell’s three-link swimmer. Phys. Rev. Lett. 98 (6), 068105.CrossRefGoogle ScholarPubMed
Tam, D. & Hosoi, A. E. 2011 Optimal feeding and swimming gaits of biflagellated organisms. Proc. Natl Acad. Sci. USA 108 (3), 1001–1006.CrossRefGoogle ScholarPubMed
van Rees, W. M., Gazzola, M. & Koumoutsakos, P. 2015 Optimal morphokinematics for undulatory swimmers at intermediate Reynolds numbers. J. Fluid Mech. 775, 178–188.CrossRefGoogle Scholar
Was, L. & Lauga, E. 2014 Optimal propulsive flapping in Stokes flows. Bioinspir. Biomim. 9 (1), 016001.Google ScholarPubMed
Weymouth, G. D. & Triantafyllou, M. S. 2013 Ultra-fast escape of a deformable jet-propelled body. J. Fluid Mech. 721, 367–385.CrossRefGoogle Scholar
Xu, M. & Wei, M. 2016 Using adjoint-based optimization to study kinematics and deformation of flapping wings. J. Fluid Mech. 799, 56–99.CrossRefGoogle Scholar