Hostname: page-component-7479d7b7d-qs9v7 Total loading time: 0 Render date: 2024-07-13T06:37:23.888Z Has data issue: false hasContentIssue false
  • English
  • Français

Baroclinic critical layer in a viscous stratified boundary layer flow on an undulated tilted surface

Published online by Cambridge University Press:  01 March 2023

Sarah Christin Open the ORCID record for Sarah Christin [Opens in a new window] ,
Patrice Meunier Open the ORCID record for Patrice Meunier [Opens in a new window]  and
Stéphane Le Dizès Open the ORCID record for Stéphane Le Dizès [Opens in a new window]
Sarah Christin
Affiliation:
Aix-Marseille Université, CNRS, Centrale Marseille, IRPHE, Marseille, France
Patrice Meunier*
Affiliation:
Aix-Marseille Université, CNRS, Centrale Marseille, IRPHE, Marseille, France
Stéphane Le Dizès
Affiliation:
Aix-Marseille Université, CNRS, Centrale Marseille, IRPHE, Marseille, France
*
†Email address for correspondence: meunier@irphe.univ-mrs.fr
Get access Rights & Permissions [Opens in a new window]

Abstract

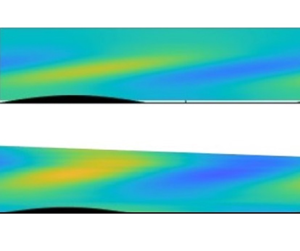
The present paper investigates theoretically and experimentally the boundary layer generated by a stably stratified fluid flowing horizontally along a surface tilted in the transverse direction and deformed by sinusoidal undulations with crests perpendicular to the flow direction. In the absence of undulations, a weak transverse velocity proportional to the normal velocity is created such that the flow remains purely horizontal. In the presence of undulations of amplitude $h$, a stronger transverse flow is generated that exhibits a singular behaviour at the critical altitude where the frequency of the perturbation matches the buoyancy frequency of the fluid. This baroclinic critical layer was previously analysed by Passaggia et al. (J. Fluid Mech., vol. 751, 2014, pp. 663–684) for a boundary layer flow with a small sliding velocity on the surface. Here, the no-slip boundary condition of the experimental flow is applied. For this purpose, we solve the viscous sub-layer to obtain a complete theoretical model for the solution in the critical layer without any adjusting parameter. The theoretical predictions for the transverse velocity are compared with experimental measurements, and a good quantitative agreement is demonstrated. Compared with the sliding case, the no-slip boundary condition on the surface reduces the amplitude of the critical layer solution by a factor $Re^{-1/3}$, where the Reynolds number Re is defined using the velocity at infinity and the thickness of the boundary layer. As a consequence, the transverse velocity has a maximum in the critical layer of order $h$, but it still induces a shear rate of order $h\,Re^{1/3}$.

JFM classification

Geophysical and Geological Flows: Stratified flows Geophysical and Geological Flows: Topographic effects Waves/Free-surface Flows: Critical layers
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 958 , 10 March 2023 , A13
Check for updates
Copyright
© The Author(s), 2023. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Baines, P.G. 2001 Mixing in flows down gentle slopes into stratified environments. J. Fluid Mech. 443, 237–270.CrossRefGoogle Scholar
Baines, P.G. 2005 Mixing regimes for the flow of dense fluid down slopes into stratified environments. J. Fluid Mech. 538, 245–267.CrossRefGoogle Scholar
Baines, P.G. & Condie, S. 1998 Observations and modeling of antarctic downslope flows: a review. Antar. Res. S. 75, 29–49.Google Scholar
Beckebanze, F., Brouzet, C., Sibgatullin, I. & Maas, L. 2018 Damping of quasi-two-dimensional internal wave attractors by rigid-wall friction. J. Fluid Mech. 841, 614–635.CrossRefGoogle Scholar
Bosco, M. 2015 Etude du sillage stratifié d'un cylindre. PhD thesis, Aix-Marseille Université.Google Scholar
Boulanger, N., Meunier, P. & Le Dizès, S. 2007 Structure of a tilted stratified vortex. J. Fluid Mech. 583, 443–458.CrossRefGoogle Scholar
Boulanger, N., Meunier, P. & Le Dizès, S. 2008 Tilt-induced instability of a stratified vortex. J. Fluid Mech. 596, 1–20.CrossRefGoogle Scholar
Bühler, O. 2014 Waves and Mean Flows. Cambridge University Press.CrossRefGoogle Scholar
Candelier, J., Le Dizès, S. & Millet, C. 2012 Inviscid instability of a stably stratified compressible boundary layer on an inclined surface. J. Fluid Mech. 694, 524–539.CrossRefGoogle Scholar
Chen, J., Bai, Y & Le Dizès, S. 2016 Instability of a boundary layer flow on a vertical wall in a stably stratified fluid. J. Fluid Mech. 795, 262–277.CrossRefGoogle Scholar
Christin, S. 2021 Etudes expérimentales en fluide stratifié: couche limite et interactions fluide-structure. PhD thesis, Aix-Marseille Université.Google Scholar
Davis, G., Dauxois, T., Jamin, T. & Joubaud, S. 2019 Energy budget in internal wave attractor experiments. J. Fluid Mech. 880, 743–763.CrossRefGoogle Scholar
Dong, M., Liu, Y. & Wu, X. 2020 Receptivity of inviscid modes in supersonic boundary layers due to scattering of free-stream sound by localised wall roughness. J. Fluid Mech. 896, A23.CrossRefGoogle Scholar
Drazin, P.G. & Reid, W.H. 1999 Hydrodynamic Stability. Cambridge University Press.Google Scholar
Garrett, C. & Kunze, E. 2007 Internal tide generation in the deep ocean. Annu. Rev. Fluid Mech. 29, 57–87.CrossRefGoogle Scholar
Garrett, C., MacCready, P. & Rhines, P. 1993 Boundary mixing and arrested Ekman layers: rotating stratified flow near a sloping boundary. Annu Rev. Fluid Mech. 25 (1), 291–323.CrossRefGoogle Scholar
Kuhlbrodt, T., Griesel, A., Montoya, M., Levermann, A., Hofmann, M. & Rahmstorf, S. 2007 On the driving processes of the atlantic meridional overturning circulation. Rev. Geophys. 45, RG2001.CrossRefGoogle Scholar
Le Dizès, S. 2020 Reflection of oscillating internal shear layers: nonlinear corrections. J. Fluid Mech. 899, A21.CrossRefGoogle Scholar
Le Dizès, S. & Billant, P. 2009 Radiative instability in stratified vortices. Phys. Fluids 21, 096602.CrossRefGoogle Scholar
Legg, S. 2021 Mixing by oceanic lee waves. Annu. Rev. Fluid Mech. 53, 173–201.CrossRefGoogle Scholar
Lin, C.C. 1955 The Theory of Hydrodynamic Stability. Cambridge University Press.Google Scholar
Lindzen, R.S. & Barker, J.W. 1985 Instability and wave over-reflection in stably stratified shear flow. J. Fluid Mech. 151, 189–217.CrossRefGoogle Scholar
MacCready, P. & Pawlak, G. 2001 Stratified flow along a corrugated slope: separation drag and wave drag. J. Phys. Oceangr. 31 (10), 2824–2839.2.0.CO;2>CrossRefGoogle Scholar
Marcus, P.S., Pei, S., Jiang, C.-H. & Hassanzadeh, P. 2013 Three-dimensional vortices generated by self-replication in stably stratified rotating shear flows. Phys. Rev. Lett. 111, 084501.CrossRefGoogle ScholarPubMed
Monti, P., Fernando, H.J.S., Princevac, M., Chan, W.C., Kowalewski, T.A. & Pardyjak, E.R. 2002 Observations of flow and turbulence in the nocturnal boundary layer over a slope. J. Atmos. Sci. 59 (17), 2513–2534.2.0.CO;2>CrossRefGoogle Scholar
Passaggia, P.-Y., Meunier, P. & Le Dizès, S. 2014 Response of a stratified boundary layer on a tilted wall to surface undulations. J. Fluid Mech. 751, 663–684.CrossRefGoogle Scholar
Phillips, O.M., Shyu, J.-H. & Salmun, H. 1986 An experiment on boundary mixing: mean circulation and transport rates. J. Fluid Mech. 173, 473–499.CrossRefGoogle Scholar
Puthan, P., Jalali, M., Chalamalla, V.K. & Sarkar, S. 2019 Energetics and mixing in buoyancy-driven near-bottom stratified flow. J. Fluid Mech. 869, 214–237.CrossRefGoogle Scholar
Rebesco, M., Hernández-Molina, F.J., Van Rooij, D. & Wåhlin, A. 2014 Contourites and associated sediments controlled by deep-water circulation processes: state-of-the-art and future considerations. Mar. Geol. 352, 111–154.CrossRefGoogle Scholar
Schlichting, H. 1979 Boundary-Layer Theory. McGraw-Hill.Google Scholar
Sen, A., Scott, R.B. & Arbic, B.K. 2008 Global energy dissipation rate of deep-ocean low-frequency flows by quadratic bottom boundary layer drag: computations from current-meter data. Geophys. Res. Lett. 35, L09606.CrossRefGoogle Scholar
Shapiro, G.I., Huthnance, J.M. & Ivanov, V.V. 2003 Dense water cascading off the continental shelf. J. Geophys. Res. 108 (C12), 3390.CrossRefGoogle Scholar
Smith, F.T. 1973 Laminar flow over a small hump on a flat plat. J. Fluid Mech. 57, 803–824.CrossRefGoogle Scholar
Thompson, A.F., Stewart, A.L., Spence, P. & Heywood, K.J. 2018 The antarctic slope current in a changing climate. Rev. Geophys. 56 (4), 741–770.CrossRefGoogle Scholar
Wang, C. & Balmforth, N. 2020 Nonlinear dynamics of forced baroclinic critical layers. J. Fluid Mech. 883, A12.CrossRefGoogle Scholar
Wang, C. & Balmforth, N. 2021 Nonlinear dynamics of forced baroclinic critical layers II. J. Fluid Mech. 917, A48.CrossRefGoogle Scholar
Wu, X. & Zhang, J. 2008 a Instability of a stratified boundary layer and its coupling with internal gravity waves. Part 1. Linear and nonlinear instabilities. J. Fluid Mech. 595, 379–408.CrossRefGoogle Scholar
Wu, X. & Zhang, J. 2008 b Instability of a stratified boundary layer and its coupling with internal gravity waves. Part 2. Coupling with internal gravity waves via topography. J. Fluid Mech. 595, 409–433.CrossRefGoogle Scholar