Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-21T04:25:36.387Z Has data issue: false hasContentIssue false
  • English
  • Français

Behaviour of small-scale turbulence in the turbulent/non-turbulent interface region of developing turbulent jets

Published online by Cambridge University Press:  20 September 2019

M. Breda Open the ORCID record for M. Breda [Opens in a new window]  and
O. R. H. Buxton Open the ORCID record for O. R. H. Buxton [Opens in a new window]
M. Breda
Affiliation:
Department of Aeronautics, Imperial College London, London SW7 2AZ, UK
O. R. H. Buxton*
Affiliation:
Department of Aeronautics, Imperial College London, London SW7 2AZ, UK
*
†Email address for correspondence: o.buxton@imperial.ac.uk
Get access Rights & Permissions [Opens in a new window]

Abstract

Tomographic particle image velocimetry experiments were conducted in the near and intermediate fields of two different types of jet, one fitted with a circular orifice and another fitted with a repeating-fractal-pattern orifice. Breda & Buxton (J. Vis., vol. 21 (4), 2018, pp. 525–532; Phys. Fluids, vol. 30, 2018, 035109) showed that this fractal geometry suppressed the large-scale coherent structures present in the near field and affected the rate of entrainment of background fluid into, and subsequent development of, the fractal jet, relative to the round jet. In light of these findings we now examine the modification of the turbulent/non-turbulent interface (TNTI) and spatial evolution of the small-scale behaviour of these different jets, which are both important factors behind determining the entrainment rate. This evolution is examined in both the streamwise direction and within the TNTI itself where the fluid adapts from a non-turbulent state, initially through the direct action of viscosity and then through nonlinear inertial processes, to the state of the turbulence within the bulk of the flow over a short distance. We show that the suppression of the coherent structures in the fractal jet leads to a less contorted interface, with large-scale excursions of the inner TNTI (that between the jet’s azimuthal shear layer and the potential core) being suppressed. Further downstream, the behaviour of the TNTI is shown to be comparable for both jets. The velocity gradients develop into a canonical state with streamwise distance, manifested as the development of the classical tear-drop shaped contours of the statistical distribution of the velocity-gradient-tensor invariants 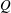$\mathit{Q}$ and 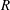$\mathit{R}$. The velocity gradients also develop spatially through the TNTI from the irrotational boundary to the bulk flow; in particular, there is a strong small-scale anisotropy in this region. This strong inhomogeneity of the velocity gradients in the TNTI region has strong consequences for the scaling of the thickness of the TNTI in these spatially developing flows since both the Taylor and Kolmogorov length scales are directly computed from the velocity gradients.

JFM classification

Turbulent Flows: Shear layer turbulence Mixing: Turbulent mixing
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 879 , 25 November 2019 , pp. 187 - 216
Check for updates
Copyright
© 2019 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Attili, A., Cristancho, J. C. & Bisetti, F. 2014 Statistics of the turbulent/non-turbulent interface in a spatially developing mixing layer. J. Turbul. 15 (9), 555–568.10.1080/14685248.2014.919394Google Scholar
Bechlars, P. & Sandberg, R. D. 2017 Variation of enstrophy production and strain rotation relation in a turbulent boundary layer. J. Fluid Mech. 812, 321–348.10.1017/jfm.2016.794Google Scholar
Betchov, R. 1956 An inequality concerning the production of vorticity in isotropic turbulence. J. Fluid Mech. 1 (5), 497–504.10.1017/S0022112056000317Google Scholar
Bisset, D. K., Hunt, J. C. R. & Rogers, M. M. 2002 The turbulent/non-turbulent interface bounding a far wake. J. Fluid Mech. 451, 383–410.10.1017/S0022112001006759Google Scholar
Blackburn, H. M., Mansour, N. N. & Cantwell, B. J. 1996 Topology of fine-scale motions in turbulent channel flow. J. Fluid Mech. 310, 269–292.10.1017/S0022112096001802Google Scholar
Breda, M. & Buxton, O. R. H. 2018a Effects of multiscale geometry on the large-scale coherent structures of an axisymmetric turbulent jet. J. Vis. 21 (4), 525–532.Google Scholar
Breda, M. & Buxton, O. R. H. 2018b Influence of coherent structures on the evolution of an axisymmetric turbulent jet. Phys. Fluids 30, 035109.10.1063/1.5019668Google Scholar
Buxton, O. R. H. 2015 Modulation of the velocity gradient tensor by concurrent large-scale velocity fluctuations in a turbulent mixing layer. J. Fluid Mech. 777, 1–12.10.1017/jfm.2015.357Google Scholar
Buxton, O. R. H., Breda, M. & Chen, X. 2017 Invariants of the velocity-gradient tensor in a spatially developing inhomogeneous turbulent flow. J. Fluid Mech. 817, 1–20.10.1017/jfm.2017.93Google Scholar
Buxton, O. R. H., Breda, M. & Dhall, K. 2019 Importance of small-scale anisotropy in the turbulent/nonturbulent interface region of turbulent free shear flows. Phys. Rev. Fluids 4 (3), 34603.10.1103/PhysRevFluids.4.034603Google Scholar
Buxton, O. R. H. & Ganapathisubramani, B. 2010 Amplification of enstrophy in the far field of an axisymmetric turbulent jet. J. Fluid Mech. 651, 483–502.10.1017/S0022112009993892Google Scholar
Buxton, O. R. H., Laizet, S. & Ganapathisubramani, B. 2011 The effects of resolution and noise on kinematic features of fine-scale turbulence. Exp. Fluids 51, 1417–1437.10.1007/s00348-011-1159-2Google Scholar
Chacin, J. M. & Cantwell, B. J. 2000 Dynamics of a low Reynolds number turbulent boundary layer. J. Fluid Mech. 404, 87–115.10.1017/S002211209900720XGoogle Scholar
Cheng, W.1996 Study of the velocity gradient tensor in turbulent flows. PhD thesis, Stanford University.Google Scholar
Chertkov, M., Pumir, A. & Shraiman, B. I. 1999 Lagrangian tetrad dynamics and the phenomenology of turbulence. Phys. Fluids 11 (8), 2394–2410.10.1063/1.870101Google Scholar
Chong, M. S., Perry, A. E. & Cantwell, B. J. 1990 A general classification of threedimensional flow fields. Phys. Fluids A 2 (5), 765–777.10.1063/1.857730Google Scholar
Corrsin, S. & Kistler, A. L.1954 Free-stream boundaries of turbulent flows NACA Tech. Rep. Google Scholar
Dahm, W. J. A. & Dimotakis, P. E. 1987 Measurements of entrainment and mixing in turbulent jets. AIAA J. 25 (9), 1216–1223.10.2514/3.9770Google Scholar
De Silva, C. M., Philip, J. & Marusic, I. 2013 Minimization of divergence error in volumetric velocity measurements and implications for turbulence statistics. Exp. Fluids 54 (7), 1–17.Google Scholar
Dimotakis, P. E. 2000 The mixing transition in turbulent flows. J. Fluid Mech. 409, 69–98.10.1017/S0022112099007946Google Scholar
Discetti, S. & Astarita, T. 2012 Fast 3D PIV with direct sparse cross-correlations. Exp. Fluids 53, 1437–1451.10.1007/s00348-012-1370-9Google Scholar
Elsinga, G. E., Ishihara, T., Goudar, M. V., Da Silva, C. B. & Hunt, J. C. R. 2017 The scaling of straining motions in homogeneous isotropic turbulence. J. Fluid Mech. 829, 31–64.10.1017/jfm.2017.538Google Scholar
Elsinga, G. E. & Marusic, I. 2010 Universal aspects of small-scale motions in turbulence. J. Fluid Mech. 662, 514–539.10.1017/S0022112010003381Google Scholar
Fiscaletti, D., Attili, A., Bisetti, F. & Elsinga, G. E. 2016a Scale interactions in a mixing layer the role of the large-scale gradients. J. Fluid Mech. 791, 154–173.10.1017/jfm.2016.53Google Scholar
Fiscaletti, D., Elsinga, G. E., Attili, A., Bisetti, F. & Buxton, O. R. H. 2016b Scale dependence of the alignment between strain rate and rotation in turbulent shear flow. Phys. Rev. Fluids 1, 064405.10.1103/PhysRevFluids.1.064405Google Scholar
Gomes-Fernandes, R., Ganapathisubramani, B. & Vassilicos, J. C. 2014 Evolution of the velocity-gradient tensor in a spatially developing turbulent flow. J. Fluid Mech. 756, 252–292.10.1017/jfm.2014.452Google Scholar
Goto, S. & Vassilicos, J. C. 2016 Local equilibrium hypothesis and Taylor’s dissipation law. Fluid Dyn. Res. 48, 021402.Google Scholar
Hamlington, P. E., Schumacher, J. & Dahm, W. J. A. 2008 Direct assessment of vorticity alignment with local and nonlocal strain rates in turbulent flows. Phys. Fluids 20, 111703.10.1063/1.3021055Google Scholar
Herman, G. T. & Lent, A. 1976 Iterative reconstruction algorithms. Comput. Biol. Med. 6, 273–294.10.1016/0010-4825(76)90066-4Google Scholar
Ho, C. & Gutmark, E. 1987 Vortex induction and mass entrainment in a small-aspect-ratio elliptic jet. J. Fluid Mech. 179, 383–405.10.1017/S0022112087001587Google Scholar
Holzner, M. & Lüthi, B. 2011 Laminar superlayer at the turbulence boundary. Phys. Rev. Lett. 106, 134503.10.1103/PhysRevLett.106.134503Google Scholar
Hunt, J. & Durbin, P. 1999 Perturbed vortical layers and shear sheltering. Fluid Dyn. Res. 24, 375–404.10.1016/S0169-5983(99)00009-XGoogle Scholar
Ishihara, T., Kaneda, Y. & Hunt, J. C. R. 2013 Thin shear layers in high Reynolds number turbulence DNS results. Flow Turbul. Combust. 91, 895–929.10.1007/s10494-013-9499-zGoogle Scholar
Lane-Serff, G. 1993 Investigation of the fractal structure of jets and plumes. J. Fluid Mech. 249, 521–534.10.1017/S0022112093001272Google Scholar
Mandelbrot, B. B. 1982 The Fractal Geometry of Nature. W. H. Freeman and Company.Google Scholar
Mistry, D., Dawson, J. R. & Kerstein, A. R. 2018 The multi-scale geometry of the near field in an axisymmetric jet. J. Fluid Mech. 838, 501–515.10.1017/jfm.2017.899Google Scholar
Mistry, D., Philip, J., Dawson, J. R. & Marusic, I. 2016 Entrainment at multi-scales across the turbulent/non-turbulent interface in an axisymmetric jet. J. Fluid Mech. 802, 690–725.10.1017/jfm.2016.474Google Scholar
Mungal, M. G., Karasso, P. S. & Lonzano, A. 1991 The visible structure of turbulent jet diffusion flames: large-scale organization and flame tip oscillation. Combust. Sci. Technol. 76, 165–185.10.1080/00102209108951708Google Scholar
Nedić, J., Vassilicos, J. C. & Ganapathisubramani, B. 2013 Axisymmetric turbulent wakes with new nonequilibrium similarity scalings. Phys. Rev. Lett. 111, 144503.10.1103/PhysRevLett.111.144503Google Scholar
Novara, M., Batenburg, K. J. & Scarano, F. 2010 Motion tracking-enhanced MART for tomographic PIV. Meas. Sci. Technol. 21, 035401.10.1088/0957-0233/21/3/035401Google Scholar
Paul, I., Papadakis, G. & Vassilicos, J. C. 2017 Genesis and evolution of velocity gradients in near-field spatially developing turbulence. J. Fluid Mech. 815, 295–332.10.1017/jfm.2017.54Google Scholar
van Reeuwijk, M. & Holzner, M. 2014 The turbulence boundary of a temporal jet. J. Fluid Mech. 739, 254–275.10.1017/jfm.2013.613Google Scholar
da Silva, C. B. 2009 The behavior of subgrid-scale models near the turbulent/nonturbulent interface in jets. Phys. Fluids 21 (8), 081702.10.1063/1.3204229Google Scholar
da Silva, C. B., Hunt, J. C. R., Eames, I. & Westerweel, J. 2014 Interfacial layers between regions of different turbulence intensity. Annu. Rev. Fluid Mech. 46 (1), 567–590.10.1146/annurev-fluid-010313-141357Google Scholar
da Silva, C. B. & Pereira, J. C. F. 2008 Invariants of the velocity-gradient, rate-of-strain, and rate-of-rotation tensors across the turbulent/nonturbulent interface in jets. Phys. Fluids 20, 055101.10.1063/1.2912513Google Scholar
da Silva, C. B. & Taveira, R. R. 2010 The thickness of the turbulent/nonturbulent interface is equal to the radius of the large vorticity structures near the edge of the shear layer. Phys. Fluids 22, 121702.10.1063/1.3527548Google Scholar
Silva, T. S., Zecchetto, M. & da Silva, C. B. 2018 The scaling of the turbulent/non-turbulent interface at high Reynolds numbers. J. Fluid Mech. 843, 156–179.10.1017/jfm.2018.143Google Scholar
Soria, J., Sondergaard, R., Cantwell, B. J., Chong, M. S. & Perry, A. E. 1994 A study of the fine-scale motions of incompressible time-developing mixing layers. Phys. Fluids 6 (2), 871–884.10.1063/1.868323Google Scholar
Sreenivasan, K. R. & Meneveau, C. 1986 The fractal facets of turbulence. J. Fluid Mech. 173, 357–386.10.1017/S0022112086001209Google Scholar
Sreenivasan, K. R., Ramshankar, R. & Meneveau, C. 1989 Mixing, entrainment and fractal dimensions of surfaces in turbulent flows. Proc. R. Soc. Lond. A 421, 79–108.Google Scholar
Taylor, G. I. 1938 The spectrum of turbulence. Proc. R. Soc. Lond. A 164, 476–490.10.1098/rspa.1938.0032Google Scholar
Tsinober, A. 2009 An Informal Conceptual Introduction to Turbulence, 2nd edn. Springer.10.1007/978-90-481-3174-7Google Scholar
Tsinober, A., Kit, E. & Dracos, T. 1992 Experimental investigation of the field of velocity-gradients in turbulent flows. J. Fluid Mech. 242, 169–192.10.1017/S0022112092002325Google Scholar
Vieillefosse, P. 1982 Local interaction between vorticity and shear in a perfect incompressible fluid. J. de Physique 43 (6), 837–842.10.1051/jphys:01982004306083700Google Scholar
Watanabe, T., Jaulino, R., Taveira, R. R., da Silva, C. B., Nagata, K. & Sakai, Y. 2017 Role of an isolated eddy near the turbulent/non-turbulent interface layer. Phys. Rev. Fluids 2 (9), 94607.10.1103/PhysRevFluids.2.094607Google Scholar
Watanabe, T., Sakai, Y., Nagata, K., Ito, Y. & Hayase, T. 2015 Turbulent mixing of passive scalar near turbulent and non-turbulent interface in mixing layers. Phys. Fluids 27, 085109.10.1063/1.4928199Google Scholar
Westerweel, J., Fukushima, C., Pedersen, J. M. & Hunt, J. C. R. 2005 Mechanics of the turbulent-nonturbulent interface of a jet. Phys. Rev. Lett. 95, 174501.Google Scholar
Westerweel, J., Fukushima, C., Pedersen, J. M. & Hunt, J. C. R. 2009 Momentum and scalar transport at the turbulent/non-turbulent interface of a jet. J. Fluid Mech. 631, 199–230.10.1017/S0022112009006600Google Scholar
Wieneke, B. 2008 Volume self-calibration for 3D particle image velocimetry. Exp. Fluids 45, 549–556.10.1007/s00348-008-0521-5Google Scholar
Worth, N. a, Nickels, T. B. & Swaminathan, N. 2010 A tomographic PIV resolution study based on homogeneous isotropic turbulence DNS data. Exp. Fluids 49, 637–656.10.1007/s00348-010-0840-1Google Scholar
Zhou, Y. & Vassilicos, J. C. 2017 Related self-similar statistics of the turbulent/non-turbulent interface and the turbulence dissipation. J. Fluid Mech. 821, 440–457.10.1017/jfm.2017.262Google Scholar