Hostname: page-component-5cf477f64f-rdph2 Total loading time: 0 Render date: 2025-04-07T05:44:44.378Z Has data issue: false hasContentIssue false
  • English
  • Français

Boundedness of the velocity derivative skewness in various turbulent flows

Published online by Cambridge University Press:  28 September 2015

R. A. Antonia ,
S. L. Tang ,
L. Djenidi  and
L. Danaila
R. A. Antonia
Affiliation:
School of Engineering, University of Newcastle, NSW 2308, Australia
S. L. Tang
Affiliation:
School of Engineering, University of Newcastle, NSW 2308, Australia Institute for Turbulence-Noise-Vibration Interaction and Control, Shenzhen Graduate School, Harbin Institute of Technology, Shenzhen 518055, PR China
L. Djenidi*
Affiliation:
School of Engineering, University of Newcastle, NSW 2308, Australia
L. Danaila
Affiliation:
CORIA CNRS UMR 6614, Université de Rouen, 76801 Saint Etienne du Rouvray, France
*
†Email address for correspondence: lyazid.djenidi@newcastle.edu.au
Get access Rights & Permissions [Opens in a new window]

Abstract

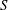The variation of $S$, the velocity derivative skewness, with the Taylor microscale Reynolds number 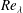$\mathit{Re}_{{\it\lambda}}$ is examined for different turbulent flows by considering the locally isotropic form of the transport equation for the mean energy dissipation rate 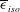$\overline{{\it\epsilon}}_{iso}$. In each flow, the equation can be expressed in the form 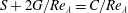$S+2G/\mathit{Re}_{{\it\lambda}}=C/\mathit{Re}_{{\it\lambda}}$, where 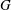$G$ is a non-dimensional rate of destruction of 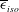$\overline{{\it\epsilon}}_{iso}$ and 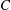$C$ is a flow-dependent constant. Since 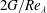$2G/\mathit{Re}_{{\it\lambda}}$ is found to be very nearly constant for 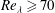$\mathit{Re}_{{\it\lambda}}\geqslant 70$, 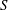$S$ should approach a universal constant when 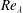$\mathit{Re}_{{\it\lambda}}$ is sufficiently large, but the way this constant is approached is flow dependent. For example, the approach is slow in grid turbulence and rapid along the axis of a round jet. For all the flows considered, the approach is reasonably well supported by experimental and numerical data. The constancy of 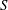$S$ at large 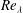$\mathit{Re}_{{\it\lambda}}$ has obvious ramifications for small-scale turbulence research since it violates the modified similarity hypothesis introduced by Kolmogorov (J. Fluid Mech., vol. 13, 1962, pp. 82–85) but is consistent with the original similarity hypothesis (Kolmogorov, Dokl. Akad. Nauk SSSR, vol. 30, 1941, pp. 299–303).

JFM classification

Turbulent Flows: Turbulence theory Turbulent Flows: Turbulent Flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 781 , 25 October 2015 , pp. 727 - 744
Check for updates
Copyright
© 2015 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abe, H., Antonia, R. A. & Kawamura, H. 2009 Correlation between small-scale velocity and scalar fluctuations in a turbulent channel flow. J. Fluid Mech. 627, 1–32.CrossRefGoogle Scholar
Antonia, R. A. & Burattini, P. 2006 Approach to the $4/5$ law in homogeneous isotropic turbulence. J. Fluid Mech. 550, 175–184.CrossRefGoogle Scholar
Antonia, R. A., Djenidi, L. & Danaila, L. 2014 Collapse of the turbulent dissipation range on Kolmogorov scales. Phys. Fluids 26, 045105.Google Scholar
Antonia, R. A. & Orlandi, P. 2004 Similarity of decaying isotropic turbulence with a passive scalar. J. Fluid Mech. 505, 123–151.Google Scholar
Antonia, R. A. & Pearson, B. R. 2000 Reynolds number dependence of velocity structure functions in a turbulent pipe flow. Flow Turbul. Combust. 64, 95–117.Google Scholar
Antonia, R. A., Zhou, T., Danaila, L. & Anselmet, F. 2000 Streamwise inhomogeneity of decaying grid turbulence. Phys. Fluids 12, 3086–3089.CrossRefGoogle Scholar
Batchelor, G. 1953 The Theory of Homogeneous Turbulence. Cambridge University Press.Google Scholar
Batchelor, G. K. & Townsend, A. A. 1947 Decay of vorticity in isotropic turbulence. Proc. R. Soc. Lond. A 190, 534–550.Google Scholar
Belin, F., Maurer, J., Tabeling, P. & Willaime, H. 1997 Velocity gradient distributions in fully developed turbulence: experimental study. Phys. Fluids 9, 3843–3850.Google Scholar
Bos, W. J. T., Chevillard, L., Scott, J. F. & Rubinstein, R. 2012 Reynolds number effect on the velocity increment skewness in isotropic turbulence. Phys. Fluids 24, 015108.Google Scholar
Burattini, P., Antonia, R. A. & Danaila, L. 2005 Similarity in the far field of a turbulent round jet. Phys. Fluids 17, 025101.Google Scholar
Burattini, P., Lavoie, P. & Antonia, R. A. 2008 Velocity derivative skewness in isotropic turbulence and its measurement with hot wires. Exp. Fluids 45, 523–535.Google Scholar
Champagne, F. H. 1978 The fine-scale structure of the turbulent velocity field. J. Fluid Mech. 86, 67–108.Google Scholar
Champagne, F. H., Friehe, C. A., LaRue, J. C. & Wyngaard, J. C. 1977 Flux measurements, flux estimation techniques, and fine scale turbulence measurements in the unstable surface layer over land. J. Atmos. Sci. 34, 515–530.Google Scholar
Danaila, L., Anselmet, F., Zhou, T. & Antonia, R. A. 1999 A generalization of Yaglom’s equation which accounts for the large-scale forcing in heated decaying turbulence. J. Fluid Mech. 391, 359–372.Google Scholar
Danaila, L. & Antonia, R. A. 2009 Spectrum of a passive scalar in moderate Reynolds number homogeneous isotropic turbulence. Phys. Fluids 21, 111702.Google Scholar
Djenidi, L. & Antonia, R. A. 2015 A general self-preservation analysis for decaying homogeneous isotropic turbulence. J. Fluid Mech. 773, 345–365.Google Scholar
Djenidi, L., Tardu, S., Antonia, R. & Danaila, L. 2014 Breakdown of Kolmogorov’s first similarity hypothesis in grid turbulence. J. Turbul. 15, 596–610.Google Scholar
Friehe, C. A., Van Atta, C. W. & Gibson, C. H. 1971 Jet turbulence: dissipation rate measurements and correlations. AGARD Turbul. Shear Flows 18, 1–7.Google Scholar
Frisch, U. 1995 Turbulence: The Legacy of A. N. Kolmogorov. Cambridge University Press.Google Scholar
Frisch, U., Sulem, P. L. & Nelkin, M. 1978 A simple dynamical model of intermittent fully developed turbulence. J. Fluid Mech. 87, 719–736.Google Scholar
Fukayama, D., Oyamada, T., Nakano, T., Gotoh, T. & Yamamoto, K. 2000 Longitudinal structure functions in decaying and forced turbulence. J. Phys. Soc. Japan 69, 701–715.Google Scholar
Gauding, M.2014 Statistics and scaling laws of turbulent scalar mixing at high Reynolds numbers. PhD thesis, RWTH Aachen University.Google Scholar
George, W. K. 1992 The decay of homogeneous isotropic turbulence. Phys. Fluids 5, 1–29.Google Scholar
George, W. K., Wang, H., Wollblad, C. & Johansson, T. G.2001 ‘Homogeneous turbulence’ and its relation to realizable flows. In 14th Australasian Fluid Mechanics Conference, Adelaide University, Adelaide, Australia.Google Scholar
Gibson, C. H., Stegen, G. R. & Williams, R. B. 1970 Statistics of the fine structure of turbulent velocity and temperature fields at high Reynolds number. J. Fluid Mech. 41, 153–167.Google Scholar
Gotoh, T., Fukayama, D. & Nakano, T. 2002 Velocity field statistics in homogeneous steady turbulence obtained using a high-resolution direct numerical simulation. Phys. Fluids 14, 1065–1081.CrossRefGoogle Scholar
Ishihara, T., Gotoh, T. & Kaneda, Y. 2009 Study of high-Reynolds number isotropic turbulence by direct numerical simulation. Annu. Rev. Fluid Mech. 41, 165–180.CrossRefGoogle Scholar
Ishihara, T., Kaneda, Y., Yokokawa, M., Itakura, K. & Uno, A. 2005 Energy spectrum in the near dissipation range of high resolution direct numerical simulation of turbulence. J. Phys. Soc. Japan 72, 983–986.Google Scholar
Ishihara, T., Kaneda, Y., Yokokawa, M., Itakura, K. & Uno, A. 2007 Small-scale statistics in high-resolution direct numerical simulation of turbulence: Reynolds number dependence of one-point velocity gradient statistics. J. Fluid Mech. 592, 335–366.CrossRefGoogle Scholar
Jimenez, J., Wray, A. A., Saffman, P. G. & Rogallo, R. S. 1993 The structure of intense vorticity in isotropic turbulence. J. Fluid Mech. 255, 65–90.Google Scholar
Kahalerras, H., Malecot, Y. & Gagne, Y. 1998 Intermittency and Reynolds number. Phys. Fluids 10, 910–921.Google Scholar
Karman, T. & Howarth, L. 1938 On the statistical theory of isotropic turbulence. Proc. R. Soc. Lond. A 164, 192–215.Google Scholar
Kerr, R. M. 1985 Higher-order derivative correlations and the alignment of small-scale structures in isotropic numerical turbulence. J. Fluid Mech. 153, 31–58.Google Scholar
Kolmogorov, A. N. 1941a Local structure of turbulence in an incompressible fluid for very large Reynolds numbers. Dokl. Akad. Nauk SSSR 30, 299–303.Google Scholar
Kolmogorov, A. N. 1941b Dissipation of energy in the locally isotropic turbulence. Dokl. Akad. Nauk SSSR 32, 19–21.Google Scholar
Kolmogorov, A. N. 1962 A refinement of previous hypotheses concerning the local structure of turbulence in a viscous incompressible fluid at high Reynolds number. J. Fluid Mech. 13, 82–85.Google Scholar
Larssen, J. V. & Devenport, W. J. 2011 On the generation of large-scale homogeneous turbulence. Exp. Fluids 50, 1207–1223.Google Scholar
Lavoie, P., Djenidi, L. & Antonia, R. A. 2007 Effects of initial conditions in decaying turbulence generated by passive grids. J. Fluid Mech. 585, 395–420.Google Scholar
Lee, S. K., Djenidi, L., Antonia, R. A. & Danaila, L. 2013 On the destruction coefficients for slightly heated decaying grid turbulence. Intl J. Heat Fluid Flow 43, 129–136.Google Scholar
Lefeuvre, N., Djenidi, L. & Antonia, R. A.2015 Decay of mean energy dissipation rate on the axis of a turbulent round jet. In The 9th Symposium on Turbulence and Shear Flow Phenomena (TSFP-9), Melbourne, Australia.Google Scholar
Lindborg, E. 1999 Correction to the four-fifths law due to variations of the dissipation. Phys. Fluids 11, 510–512.Google Scholar
Mansour, N. N. & Wray, A. A. 1994 Decay of isotropic turbulence at low Reynolds number. Phys. Fluids 6, 808–813.Google Scholar
Meldi, M. & Sagaut, P. 2013 Further insights into self-similarity and self-preservation in freely decaying isotropic turbulence. J. Turbul. 14, 24–53.Google Scholar
Mi, J., Xu, M. & Zhou, T. 2013 Reynolds number influence on statistical behaviors of turbulence in a circular free jet. Phys. Fluids 25, 075101.Google Scholar
Moisy, F., Tabeling, P. & Willaime, H. 1999 Kolmogorov equation in a fully developed turbulence experiment. Phys. Rev. Lett. 82, 3994–3997.Google Scholar
Mydlarski, L. & Warhaft, Z. 1996 On the onset of high-Reynolds-number grid-generated wind tunnel turbulence. J. Fluid Mech. 320, 331–368.Google Scholar
Pope, S. B. 2000 Turbulent Flows. Cambridge University Press.Google Scholar
Qian, J. 1986 A closure theory of intermittency of turbulence. Phys. Fluids 29, 2165–2171.Google Scholar
Qian, J. 1994 Skewness factor of turbulent velocity derivative. Acta Mechanica Sin. 10, 12–15.Google Scholar
Qian, J. 1999 Slow decay of the finite Reynolds number effect of turbulence. Phys. Rev. E 60, 3409–3412.Google Scholar
Qian, J. 2003 An equality about the velocity derivative skewness in turbulence. Phys. Fluids 15, 1005–1011.Google Scholar
Rosenberg, B. J., Hultmark, M., Vallikivi, M., Bailey, S. C. C. & Smits, A. J. 2013 Turbulence spectra in smooth- and rough-wall pipe flow at extreme Reynolds numbers. J. Fluid Mech. 731, 46–63.Google Scholar
Saddoughi, S. G. & Veeravalli, S. V. 1994 Local isotropy of turbulent boundary layers at high Reynolds number. J. Fluid Mech. 268, 333–372.CrossRefGoogle Scholar
Saffman, P. G. 1970 Dependence on Reynolds number of high-order moments of velocity derivatives in isotropic turbulence. Phys. Fluids 13, 2193–2194.Google Scholar
Speziale, C. G. & Bernard, P. S. 1992 The energy decay in self-preserving isotropic turbulence revisited. J. Fluid Mech. 241, 645–667.Google Scholar
Sreenivasan, K. & Antonia, R. A. 1997 The phenomenology of small-scale turbulence. Annu. Rev. Fluid Mech. 29, 435–472.Google Scholar
Tabeling, P., Zocchi, G., Belin, F., Maurer, J. & Willaime, H. 1996 Probability density functions, skewness, and flatness in large Reynolds number turbulence. Phys. Rev. E 53, 1613–1621.Google Scholar
Tang, S. L., Antonia, R. A., Djenidi, L., Abe, H., Zhou, T., Danaila, L. & Zhou, Y. 2015b Transport equation for the mean turbulent energy dissipation rate on the centreline of a fully developed channel flow. J. Fluid Mech. 777, 151–177.Google Scholar
Tang, S. L., Antonia, R. A., Djenidi, L. & Zhou, Y.2015a Consequence of self-preservation in a turbulent far-wake. In The 9th Symposium on Turbulence and Shear Flow Phenomena (TSFP-9), Melbourne, Australia.Google Scholar
Tennekes, H. 1968 Simple model for the small-scale structure of turbulence. Phys. Fluids 11, 669–671.Google Scholar
Thiesset, F., Antonia, R. A. & Djenidi, L. 2014 Consequences of self-preservation on the axis of a turbulent round jet. J. Fluid Mech. 748, R2.Google Scholar
Van Atta, C. W. & Antonia, R. A. 1980 Reynolds number dependence of skewness and flatness factors of turbulent velocity derivatives. Phys. Fluids 23, 252–257.Google Scholar
Wyngaard, J. C. & Tennekes, H. 1970 Measurements of the small-scale structure of turbulence at moderate Reynolds numbers. J. Fluid Mech. 13, 1962–1969.Google Scholar
Yeung, P. K. & Zhou, Y. 1997 Universality of the Kolmogorov constant in numerical simulations of turbulence. Phys. Rev. E 56, 1746–1752.Google Scholar
Yoffe, S.2012 Investigation of the transfer and dissipation of energy in isotropic turbulence. PhD thesis, University of Edinburgh. http://arxiv.org/pdf/1306.3408v1.pdf.Google Scholar
Zhou, T. & Antonia, R. A. 2000 Reynolds number dependence of the small-scale structure of grid turbulence. J. Fluid Mech. 406, 81–107.Google Scholar
Zhou, T., Antonia, R. A. & Chua, L. P. 2005 Flow and Reynolds number dependencies of one-dimensional vorticity fluctuations. J. Turbul. 6, 1–17.Google Scholar