Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-26T07:27:47.345Z Has data issue: false hasContentIssue false
  • English
  • Français

Buoyant Tsuji diffusion flames: global flame structure and flow field

Published online by Cambridge University Press:  18 May 2020

Mariovane S. Donini Open the ORCID record for Mariovane S. Donini [Opens in a new window] ,
Cesar F. Cristaldo Open the ORCID record for Cesar F. Cristaldo [Opens in a new window]  and
Fernando F. Fachini Open the ORCID record for Fernando F. Fachini [Opens in a new window]
Mariovane S. Donini
Affiliation:
Grupo de Mecânica de Fluidos Reativos, Instituto Nacional de Pesquisas Espaciais, Cachoeira Paulista SP, Brazil
Cesar F. Cristaldo
Affiliation:
Laboratório de Fluidodinâmica Computacional e Turbulência Atmosférica,Universidade Federal do Pampa, Alegrete RS, Brazil
Fernando F. Fachini*
Affiliation:
Grupo de Mecânica de Fluidos Reativos, Instituto Nacional de Pesquisas Espaciais, Cachoeira Paulista SP, Brazil
*
†Email address for correspondence: fernando.fachini@inpe.br
Get access Rights & Permissions [Opens in a new window]

Abstract

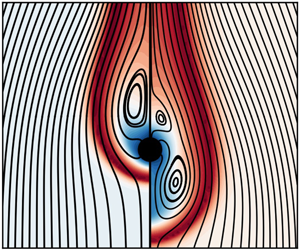
The present work analyses how buoyancy is impacting the topology of diffusion flames established around a horizontal cylindrical burner. The flow conditions are chosen such that the system is subjected to negative and positive buoyant forces. It is proposed in this study to investigate the effect of a modulation of the balance between these buoyant forces on the flame structure by varying the temperature of the ambient atmosphere. More specifically, conditions are sought for establishing a buoyant Tsuji diffusion flame characterized by a very low level of strain rate in its lower part (i.e. below the burner). To understand the fundamental mechanisms controlling the whole flame topology, a model is proposed which assumes steadiness and incompressibility of the flow while retaining buoyancy effects in the momentum balance. The results showed that an increase of the ambient temperature leads to the appearance of a counterflow zone below the burner where the flame is undergoing very low levels of strain rate. The overall flame proves to be shorter than its counterpart observed in the forced convection regime. In addition, it is shown that an order of magnitude analysis is able to recover the sensitivity of the flame behaviour to the Péclet and Froude numbers as well as to the combustion parameters. In a certain range of the ambient-atmosphere temperature, the flow field changes dramatically: for the same boundary conditions, there are two steady-state solutions which depend on the initial conditions, i.e. the system presents a hysteresis.

JFM classification

Reacting Flows: Laminar reacting flows Convection: Buoyancy-driven instability Vortex Flows: Vortex dynamics
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 895 , 25 July 2020 , A17
Copyright
© The Author(s), 2020. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bianchin, R. P., Donini, M. S., Cristaldo, C. F. C. & Fachini, F. F. 2019 On the global structure and asymptotic stability of low-stretch diffusion flame: forced convection. Proc. Combust. Inst. 37, 1903–1910.CrossRefGoogle Scholar
Bonne, U. 1971 Radiative extinguishment of diffusion flames at zero gravity. Combust. Flame 16, 147–159.CrossRefGoogle Scholar
Chorin, A. J. 1997 A numerical method for solving incompressible viscous flow problems. J. Comput. Phys. 135, 118–125.CrossRefGoogle Scholar
Fachini, F. F. 1999 An analytical solution for the quasi-steady droplet combustion. Combust. Flame 116, 302–306.Google Scholar
Fachini, F. F. 2007 Extended Shvab-Zel’dovich formulation for multicomponent-fuel diffusion flames. Intl J. Heat Mass Transfer 50, 1035–1048.CrossRefGoogle Scholar
Fachini, F. F., Liñán, A. & Williams, F. A. 1999 Theory of flame histories in droplet combustion at small stoichiometric fuel-air ratios. AIAA J. 37, 1426–1435.CrossRefGoogle Scholar
Fernandez-Pello, A. C. & Law, C. K. 1982 On the mixed-convective flame structure in the stagnation point of a fuel particle. In 19th Symposium (International) on Combustion, Technion-Israel Institute of Technology Haifa, Israel, pp. 1037–1044. Elsevier.Google Scholar
Fletcher, C. A. J. 2012 Computational Techniques for Fluid Dynamics 2: Specific Techniques for Different Flow Categories. Springer.Google Scholar
Fornberg, B. 1980 A numerical study of steady viscous flow past a circular cylinder. J. Fluid Mech. 98, 819–855.CrossRefGoogle Scholar
Han, B., Ibarreta, A. F., Sung, C. J. & T’ien, J. S. 2005 Experimental low-stretch gaseous diffusion flames in buoyancy-induced flowfields. Proc. Combust. Inst. 30, 527–535.CrossRefGoogle Scholar
Jacono, D. L., Papas, P., Matalon, M. & Monkewitz, P. A. 2005 An experimental realization of an unstrained, planar diffusion flame. Proc. Combust. Inst. 30, 501–509.CrossRefGoogle Scholar
Li, Z., Navon, I. M., Hussaini, M. Y. & Le Dimet, F.-X. 2003 Optimal control of cylinder wakes via suction and blowing. Comput. Fluids 32, 149–171.CrossRefGoogle Scholar
Liñán, A. 1991 The structure of diffusion flames. In Fluid Dynamical Aspects of Combustion Theory, Pitman Research Notes in Mathematics, p. 223. Longman.Google Scholar
Liñán, A. 2001 Diffusion-controlled combustion. In Mechanics for a New Millennium, pp. 487–502. Springer.Google Scholar
Liñán, A. & Williams, F. A. 1993 Fundamental Aspects of Combustion. Oxford University Press.Google Scholar
Qian, J. & Law, C. K. 1997 On the spreading of unsteady cylindrical diffusion flames. Combust. Flame 110, 152–162.CrossRefGoogle Scholar
Sen, U., Mukhopadhyay, A. & Sen, S. 2017 Effects of fluid injection on dynamics of flow past a circular cylinder. Eur. J. Mech. (B/Fluids) 61, 187–199.CrossRefGoogle Scholar
T’ien, J. S. 1986 Diffusion flame extinction at small stretch rates: the mechanism of radiative loss. Combust. Flame 65, 31–34.CrossRefGoogle Scholar
T’ien, J. S & Foutch, D. W. 1987 Extinction of a stagnation-point diffusion flame at reduced gravity. AIAA J. 25, 972–976.Google Scholar
Tsuji, H. 1982 Counterflow diffusion flames. Prog. Energy Combust. Sci. 8, 93–119.CrossRefGoogle Scholar
Tsuji, H. & Yamaoka, I. 1967 The counterflow diffusion flame in the forward stagnation region of a porous cylinder. In 11th Symposium (International) on Combustion, Pittsburgh, PA, pp. 979–984. Elsevier.Google Scholar