Hostname: page-component-745bb68f8f-lrblm Total loading time: 0 Render date: 2025-01-19T13:09:07.476Z Has data issue: false hasContentIssue false
  • English
  • Français

A CFD data-driven aerodynamic model for fast and precise prediction of flapping aerodynamics in various flight velocities

Published online by Cambridge University Press:  31 March 2021

Xuefei Cai ,
Dmitry Kolomenskiy Open the ORCID record for Dmitry Kolomenskiy [Opens in a new window] ,
Toshiyuki Nakata Open the ORCID record for Toshiyuki Nakata [Opens in a new window]  and
Hao Liu Open the ORCID record for Hao Liu [Opens in a new window]
Xuefei Cai
Affiliation:
Shanghai Jiao Tong University and Chiba University International Cooperative Research Center (SJTU-CU ICRC), Shanghai Jiao Tong University, 800 Dongchuan Road, Minhang District, Shanghai200240, PR China Graduate School of Engineering, Chiba University, 1-33 Yayoi-cho, Inage-ku, Chiba263-8522, Japan
Dmitry Kolomenskiy
Affiliation:
Graduate School of Engineering, Chiba University, 1-33 Yayoi-cho, Inage-ku, Chiba263-8522, Japan Global Scientific Information and Computing Center, Tokyo Institute of Technology, 2-12-1, Ookayama, Meguro-ku, Tokyo152-8550, Japan
Toshiyuki Nakata
Affiliation:
Graduate School of Engineering, Chiba University, 1-33 Yayoi-cho, Inage-ku, Chiba263-8522, Japan
Hao Liu*
Affiliation:
Shanghai Jiao Tong University and Chiba University International Cooperative Research Center (SJTU-CU ICRC), Shanghai Jiao Tong University, 800 Dongchuan Road, Minhang District, Shanghai200240, PR China Graduate School of Engineering, Chiba University, 1-33 Yayoi-cho, Inage-ku, Chiba263-8522, Japan
*
†Email address for correspondence: hliu@faculty.chiba-u.jp
Get access Rights & Permissions [Opens in a new window]

Abstract

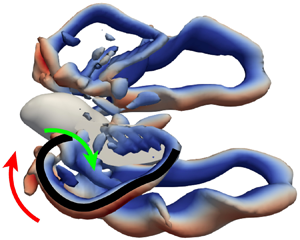
Precise prediction of unsteady flapping aerodynamics in insect flight is of potential importance in the analysis of maneuverability and flight control. While the quasi-steady model is a cheap while reasonable tool, accurate evaluation of unsteady dynamic effects in complex flight behaviours remains a challenge. Here we develop a computational fluid dynamics (CFD) data-driven aerodynamic model (CDAM), which is informed by high-fidelity CFD simulations using overset meshes to enable the precise and fast prediction of both cycle-averaged and transient aerodynamic force, torque and power with various flying motions and wing kinematics. The CDAM comprises a quasi-steady model for flapping wings and an aerodynamic model for a moving body. The least square method and a surrogate method are employed to achieve aerodynamic coefficient fitting through training using a CFD database. With comparison to CFD test data, the CDAM is validated to be capable of accurately evaluating the aerodynamic force, torque and power of a wing-body bumblebee model in various flight velocities. A genetic optimization algorithm embedded with CDAM is proposed to determine trimmed states for forward flight through adjusting wing kinematics, indicating that bumblebees likely fly in a minimized mass-specific aerodynamic power consumption. The CDAM is further applied to proportional-derivative-based longitudinal flight control of bumblebee hovering, with the control parameters optimized by Laplace transformation and the root locus method, which is implemented consistently in both CDAM and CFD environments. Our results demonstrate that CDAM provides a versatile tool to achieve fast and precise aerodynamical prediction for flying insects in various flight behaviours.

JFM classification

Biological Fluid Dynamics: Swimming/flying
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 915 , 25 May 2021 , A114
Check for updates
Copyright
© The Author(s), 2021. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Andersen, A., Pesavento, U. & Wang, Z.J. 2005 Unsteady aerodynamics of fluttering and tumbling plates. J. Fluid Mech. 541, 65–90.CrossRefGoogle Scholar
Aono, H. & Liu, H. 2006 Vortical structure and aerodynamics of hawkmoth hovering. J. Biomech. Sci. Engng 1 (1), 234–245.CrossRefGoogle Scholar
Balint, C.N. & Dickinson, M.H. 2001 The correlation between wing kinematics and steering muscle activity in the blowfly Calliphora vicina. J. Expl Biol. 204 (24), 4213–4226.Google ScholarPubMed
Beatus, T., Guckenheimer, J.M. & Cohen, I. 2015 Controlling roll perturbations in fruit flies. J. R. Soc. Interface 12 (105), 20150075.CrossRefGoogle ScholarPubMed
Berman, G.J. & Wang, Z.J. 2007 Energy-minimizing kinematics in hovering insect flight. J. Fluid Mech. 582, 153–168.CrossRefGoogle Scholar
Bluman, J. & Kang, C.K. 2017 Wing-wake interaction destabilizes hover equilibrium of a flapping insect-scale wing. Bioinspir. Biomim. 12 (4), 046004.CrossRefGoogle ScholarPubMed
Cheng, B., Fry, S.N., Huang, Q. & Deng, X. 2010 Aerodynamic damping during rapid flight maneuvers in the fruit fly drosophila. J. Expl Biol. 213 (4), 602–612.CrossRefGoogle ScholarPubMed
Cheng, X. & Sun, M. 2018 Very small insects use novel wing flapping and drag principle to generate the weight-supporting vertical force. J. Fluid Mech. 855, 646–670.CrossRefGoogle Scholar
Combes, S.A., Gagliardi, S.F., Switzer, C.M. & Dillon, M.E. 2020 Kinematic flexibility allows bumblebees to increase energetic efficiency when carrying heavy loads. Sci. Adv. 6 (6), eaay3115.CrossRefGoogle ScholarPubMed
Demoll, R. 1918 Der Flug der Insekten und der Vögel: eine Gegenüberstellung. G. Fischer.CrossRefGoogle Scholar
Deng, X., Schenato, L. & Sastry, S.S. 2006 Flapping flight for biomimetic robotic insects: part II-flight control design. IEEE Trans. Robot. 22 (4), 789–803.CrossRefGoogle Scholar
Dickinson, M.H., Lehmann, F. -O. & Sane, S.P. 1999 Wing rotation and the aerodynamic basis of insect flight. Science 284 (5422), 1954–1960.CrossRefGoogle ScholarPubMed
Dickinson, M.H. & Muijres, F.T. 2016 The aerodynamics and control of free flight manoeuvres indrosophila. Phil. Trans. R. Soc B 371 (1704), 20150388.CrossRefGoogle Scholar
Dickson, W.B. & Dickinson, M.H. 2004 The effect of advance ratio on the aerodynamics of revolving wings. J. Expl Biol. 207 (24), 4269–4281.CrossRefGoogle ScholarPubMed
Dickson, W.B., Straw, A.D., Poelma, C. & Dickinson, M.H. 2006 An integrative model of insect flight control. AIAA Paper 2006-34.CrossRefGoogle Scholar
Dudley, R. & Ellington, C.P. 1990 a Mechanics of forward flight in bumblebees: I. Kinematics and morphology. J. Expl Biol. 148 (1), 19–52.Google Scholar
Dudley, R. & Ellington, C.P. 1990 b Mechanics of forward flight in bumblebees: II. Quasi-steady lift and power requirements. J. Expl Biol. 148 (1), 53–88.Google Scholar
Dyhr, J.P., Morgansen, K.A., Daniel, T.L. & Cowan, N.J. 2013 Flexible strategies for flight control: an active role for the abdomen. J. Expl Biol. 216 (9), 1523–1536.CrossRefGoogle ScholarPubMed
Ellington, C.P. 1984 The aerodynamics of hovering insect flight. I. The quasi-steady analysis. Phil. Trans. R. Soc. Lond. B 305 (1122), 1–15.Google Scholar
Ellington, C.P. & Lighthill, M.J. 1984 The aerodynamics of hovering insect flight. IV. Aerodynamic mechanisms. Phil. Trans. R. Soc. Lond. B 305 (1122), 79–113.Google Scholar
Engels, T., Kolomenskiy, D., Schneider, K., Lehmann, F.-O. & Sesterhenn, J. 2016 a Bumblebee flight in heavy turbulence. Phys. Rev. Lett. 116 (2), 028103.CrossRefGoogle ScholarPubMed
Engels, T., Kolomenskiy, D., Schneider, K. & Sesterhenn, J. 2016 b FluSI: A novel parallel simulation tool for flapping insect flight using a fourier method with volume penalization. SIAM J. Sci. Comput. 38 (5), S3–S24.CrossRefGoogle Scholar
Evans, W.R. 1948 Graphical analysis of control systems. IEEE 67 (1), 547–551.Google Scholar
Fei, F., Tu, Z., Yang, Y., Zhang, J. & Deng, X. 2019 a Flappy hummingbird: An open source dynamic simulation of flapping wing robots and animals. In 2019 International Conference on Robotics and Automation (ICRA), pp. 9223–9229.Google Scholar
Fei, F., Tu, Z., Zhang, J. & Deng, X. 2019 b Learning extreme hummingbird maneuvers on flapping wing robots. In 2019 International Conference on Robotics and Automation (ICRA), pp. 109–115.Google Scholar
Franklin, G.F., Powell, J.D. & Emami-Naeini, A. 2014 Feedback Control of Dynamic Systems. Prentice Hall.Google Scholar
Fung, Y.C. 2008 An Introduction to the Theory of Aeroelasticity. Courier Dover Publications.Google Scholar
Glauert, H. 1983 The Elements of Aerofoil and Airscrew Theory. Cambridge University Press.CrossRefGoogle Scholar
Hansen, N. & Kern, S. 2004 Evaluating the CMA Evolution Strategy on Multimodal Test Functions, pp. 282–291. Springer.Google Scholar
Hansen, N., Müller, S.D. & Koumoutsakos, P. 2003 Reducing the time complexity of the derandomized evolution strategy with covariance matrix adaptation (CMA-ES). Evol. Comput. 11 (1), 1–18.CrossRefGoogle Scholar
Hedrick, T.L., Cheng, B. & Deng, X. 2009 Wingbeat time and the scaling of passive rotational damping in flapping flight. Science 324 (5924), 252–255.CrossRefGoogle ScholarPubMed
Hedrick, T.L. & Daniel, T.L. 2006 Flight control in the hawkmoth Manduca sexta: the inverse problem of hovering. J. Expl Biol. 209 (16), 3114–3130.CrossRefGoogle ScholarPubMed
Hengstenberg, R., Sandeman, D.C., Hengstenberg, B. & Horridge, G.A. 1986 Compensatory head roll in the blowfly calliphora during flight. Proc. R. Soc. Lond. B 227 (1249), 455–482.Google Scholar
Hoff, W. 1919 Der flug der insekten und der Vögel. Naturwissenschaften 7, 159–162.CrossRefGoogle Scholar
Ishihara, D. 2018 Role of fluid-structure interaction in generating the characteristic tip path of a flapping flexible wing. Phys. Rev. E 98, 032411.CrossRefGoogle Scholar
Jakobi, T., Kolomenskiy, D., Ikeda, T., Watkins, S., Fisher, A., Liu, H. & Ravi, S. 2018 Bees with attitude: the effects of directed gusts on flight trajectories. Biol. Open 7 (10), bio034074.CrossRefGoogle ScholarPubMed
Jensen, M. & Pringle, J.W.S. 1956 Biology and physics of locust flight. III. The aerodynamics of locust flight. Phil. Trans. R. Soc. Lond. B 239 (667), 511–552.Google Scholar
Kolomenskiy, D., et al. 2019 The dynamics of passive feathering rotation in hovering flight of bumblebees. J. Fluids Struct. 91, 102628.CrossRefGoogle Scholar
Lee, Y.J., Lua, K.B., Lim, T.T. & Yeo, K.S. 2016 A quasi-steady aerodynamic model for flapping flight with improved adaptability. Bioinspir. Biomim. 11 (3), 036005.CrossRefGoogle ScholarPubMed
Lentink, D. & Dickinson, M.H. 2009 Rotational accelerations stabilize leading edge vortices on revolving fly wings. J. Expl Biol. 212 (16), 2705–2719.CrossRefGoogle ScholarPubMed
Liu, G., Dong, H. & Li, C. 2016 a Vortex dynamics and new lift enhancement mechanism of wing–body interaction in insect forward flight. J. Fluid Mech. 795 634–651.CrossRefGoogle Scholar
Liu, H. 2002 Computational biological fluid dynamics: digitizing and visualizing animal swimming and flying. Integr. Compar. Biol. 42 (5), 1050–1059.CrossRefGoogle ScholarPubMed
Liu, H. 2009 Integrated modelling of insect flight: from morphology, kinematics to aerodynamics. J. Comput. Phys. 228 (2), 439–459.CrossRefGoogle Scholar
Liu, H. & Aono, H. 2009 Size effects on insect hovering aerodynamics: an integrated computational study. Bioinspir. Biomim. 4 (1), 015002.CrossRefGoogle Scholar
Liu, H., Ellington, C.P., Kawachi, K., Van Den Berg, C. & Willmott, A.P. 1998 A computational fluid dynamic study of hawkmoth hovering. J. Expl Biol. 201 (4), 461–477.Google ScholarPubMed
Liu, H. & Kawachi, K. 1998 A numerical study of insect flight. J. Comput. Phys. 146 (1), 124–156.CrossRefGoogle Scholar
Liu, H., Nakata, T., Gao, N., Maeda, M., Aono, H. & Shyy, W. 2010 Micro air vehicle-motivated computational biomechanics in bio-flights: aerodynamics, flight dynamics and maneuvering stability. Acta Mechanica Sin. 26 (6), 863–879.CrossRefGoogle Scholar
Liu, H., Ravi, S., Kolomenskiy, D. & Tanaka, H. 2016 b Biomechanics and biomimetics in insect-inspired flight systems. Phil. Trans. R. Soc. B 371 (1704), 20150390.CrossRefGoogle ScholarPubMed
Lophaven, S.N., Nielsen, H.B. & Søndergaard, J. 2002 DACE – a Matlab Kriging toolbox, version 2.0. Tech Rep. Informatics and Mathematical Modelling, Technical University of Denmark, DTU, Richard Petersens Plads, Building 321, DK-2800 Kgs. Lyngby.Google Scholar
Nabawy, M.R.A. & Crowther, W.J. 2014 On the quasi-steady aerodynamics of normal hovering flight part II: model implementation and evaluation. J. R. Soc. Interface 11 (94), 20131197.CrossRefGoogle ScholarPubMed
Nakata, T., Liu, H. & Bomphrey, R.J. 2015 A CFD-informed quasi-steady model of flapping-wing aerodynamics. J. Fluid Mech. 783, 323–343.CrossRefGoogle ScholarPubMed
Nakata, T., Liu, H., Tanaka, Y., Nishihashi, N., Wang, X. & Sato, A. 2011 Aerodynamics of a bio-inspired flexible flapping-wing micro air vehicle. Bioinspir. Biomim. 6 (4), 045002.CrossRefGoogle ScholarPubMed
Nguyen, T.T., Shyam Sundar, D., Yeo, K.S. & Lim, T.T. 2016 Modeling and analysis of insect-like flexible wings at low Reynolds number. J. Fluids Struct. 62, 294–317.CrossRefGoogle Scholar
Oh, S., Lee, B., Park, H., Choi, H. & Kim, S. 2020 A numerical and theoretical study of the aerodynamic performance of a hovering rhinoceros beetle (Trypoxylus dichotomus). J. Fluid Mech. 885, A18.CrossRefGoogle Scholar
Osborne, M.F.M. 1951 Aerodynamics of flapping flight with application to insects. J. Expl Biol. 28 (2), 221–245.Google ScholarPubMed
Pesavento, U. & Wang, Z.J. 2004 Falling paper: Navier–Stokes solutions, model of fluid forces, and center of mass elevation. Phys. Rev. Lett. 93 (14), 144501.CrossRefGoogle ScholarPubMed
Ravi, S., Kolomenskiy, D., Engels, T., Schneider, K., Wang, C., Sesterhenn, J. & Liu, H. 2016 Bumblebees minimize control challenges by combining active and passive modes in unsteady winds. Sci. Rep. 6, 35043.CrossRefGoogle ScholarPubMed
Sane, S.P. & Dickinson, M.H. 2002 The aerodynamic effects of wing rotation and a revised quasi-steady model of flapping flight. J. Expl Biol. 205 (8), 1087–1096.Google Scholar
Sedov, L.I. 1965 Two-dimensional Problems in Hydrodynamics and Aerodynamics. Interscience.CrossRefGoogle Scholar
Shyy, W., Aono, H., Kang, C. & Liu, H. 2013 An Introduction to Flapping Wing Aaerodynamics. Cambridge University Press.CrossRefGoogle Scholar
Shyy, W., Lian, Y., Tang, J., Viieru, D. & Liu, H. 2007 Aerodynamics of Low Reynolds Number Flyers. Cambridge University Press.Google Scholar
Sun, M., Wang, J. & Xiong, Y. 2007 Dynamic flight stability of hovering insects. Acta Mechanica Sin. 23 (3), 231–246.CrossRefGoogle Scholar
Tu, M.S. & Dickinson, M.H. 1996 The control of wing kinematics by two steering muscles of the blowfly (Calliphora vicina). J. Compar. Physiol. A 178 (6), 813–830.Google Scholar
Usherwood, J.R. & Ellington, C.P. 2002 The aerodynamics of revolving wings II. Propeller force coefficients from mayfly to quail. J. Expl Biol. 205 (11), 1565–1576.Google ScholarPubMed
Van Dalsem, W.R. & Steger, J.L. 1986 Using the boundary-layer equations in three-dimensional viscous flow simulations. In Proceedings of AGARD Fluid Dynamics Panel Symposium on Application of CFD in Aeronautics, pp. 7–10.Google Scholar
van Veen, W.G., van Leeuwen, J.L. & Muijres, F.T. 2019 A chordwise offset of the wing-pitch axis enhances rotational aerodynamic forces on insect wings: a numerical study. J. R. Soc. Interface 16 (155), 20190118.CrossRefGoogle ScholarPubMed
Wang, Q., Goosen, J.F.L. & van Keulen, F. 2016 A predictive quasi-steady model of aerodynamic loads on flapping wings. J. Fluid Mech. 800, 688–719.CrossRefGoogle Scholar
Wang, Z.J. 2004 Unsteady forces and flows in low Reynolds number hovering flight: two-dimensional computations vs robotic wing experiments. J. Expl Biol. 207 (3), 449–460.CrossRefGoogle ScholarPubMed
Weis-Fogh, T. 1973 Quick estimates of flight fitness in hovering animals, including novel mechanisms for lift production. J. Expl Biol. 59 (1), 169–230.Google Scholar
Whitney, J.P. & Wood, R.J. 2010 Aeromechanics of passive rotation in flapping flight. J. Fluid Mech. 660, 197–220.CrossRefGoogle Scholar
Willmott, A.P. & Ellington, C.P. 1997 The mechanics of flight in the hawkmoth manduca sexta. I. Kinematics of hovering and forward flight. J. Expl Biol. 200 (21), 2705–2722.Google ScholarPubMed
Xiong, Y. & Sun, M. 2008 Dynamic flight stability of a bumblebee in forward flight. Acta Mechanica Sin. 24 (1), 25–36.CrossRefGoogle Scholar
Yao, J. & Yeo, K.S. 2019 A simplified dynamic model for controlled insect hovering flight and control stability analysis. Bioinspir. Biomim. 14 (5), 056005.CrossRefGoogle ScholarPubMed
Yu, X. & Sun, M. 2009 A computational study of the wing–wing and wing–body interactions of a model insect. Acta Mechanica Sin. 25 (4), 421–431.CrossRefGoogle Scholar
Zhang, C., Hedrick, T.L. & Mittal, R. 2019 An integrated study of the aeromechanics of hovering flight in perturbed flows. AIAA J. 57 (9), 3753–3764.CrossRefGoogle Scholar
Supplementary material: File

Cai et al. supplementary material

Supplementary data (Bumblebee)

Download Cai et al. supplementary material(File)
File 243.9 MB
Supplementary material: File

Cai et al. supplementary material

Supplementary data (Hawkmoth)

Download Cai et al. supplementary material(File)
File 539.2 MB