Hostname: page-component-78c5997874-xbtfd Total loading time: 0 Render date: 2024-11-07T01:01:17.920Z Has data issue: false hasContentIssue false
  • English
  • Français

Closely spaced co-rotating helical vortices: long-wave instability

Published online by Cambridge University Press:  05 August 2022

A. Castillo-Castellanos Open the ORCID record for A. Castillo-Castellanos [Opens in a new window]  and
S. Le Dizès Open the ORCID record for S. Le Dizès [Opens in a new window]
A. Castillo-Castellanos*
Affiliation:
IRPHE, Aix Marseille Université, CNRS, Centrale Marseille, Marseille, France
S. Le Dizès
Affiliation:
IRPHE, Aix Marseille Université, CNRS, Centrale Marseille, Marseille, France
*
†Email address for correspondence: andres-alonso.castillo-castellanos@univ-amu.fr
Get access Rights & Permissions [Opens in a new window]

Abstract

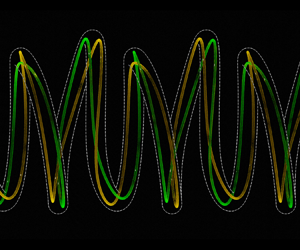
We consider as base flow the stationary vortex filament solution obtained by Castillo-Castellanos et al. (Phys. Rev. Fluids, vol. 6, 2021, 114701) in the far wake of a rotor with tip-splitting blades. The cases of a single blade and of two blades with a hub vortex are studied. In these solutions, each blade generates two closely spaced co-rotating tip vortices that form a braided helical pattern in the far wake. The long-wave stability of these solutions is analysed using the same vortex filament framework. Both the linear spectrum and the linear impulse response are considered. We demonstrate the existence of different types of instability modes. A first type corresponds to the local pairing of consecutive turns of the helical pattern, which is well described by the instability of a uniform helical vortex with a core size given by the mean separation distance of the vortices in the pair. A second type corresponds to the pairing of consecutive turns of the vortex pair and is observed only for densely braided patterns, which is well described by the instability of two interlaced helical vortices by straightening out the baseline helix. A third type of unstable modes modifies the separation distance between the vortices in each pair and amplifies specific (linear) wavelengths. These unstable modes also spread spatially with a weaker rate.

JFM classification

Vortex Flows: Vortex instability
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 946 , 10 September 2022 , A10
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Bayly, B.J. 1988 Three-dimensional centrifugal-type instabilities in inviscid two-dimensional flows. Phys. Fluids 31 (1), 56–64.CrossRefGoogle Scholar
Bhagwat, M.J. & Leishman, J.G. 2000 Stability analysis of helicopter rotor wakes in axial flight. J. Am. Helicopter Soc. 45 (3), 165–178.CrossRefGoogle Scholar
Blanco-Rodríguez, F.J. & Le Dizès, S. 2016 Elliptic instability of a curved batchelor vortex. J. Fluid Mech. 804, 224–247.CrossRefGoogle Scholar
Blanco-Rodríguez, F.J. & Le Dizès, S. 2017 Curvature instability of a curved batchelor vortex. J. Fluid Mech. 814, 397–415.CrossRefGoogle Scholar
Blanco-Rodríguez, F.J., Le Dizès, S., Selçuk, C., Delbende, I. & Rossi, M. 2015 Internal structure of vortex rings and helical vortices. J. Fluid Mech. 785, 219–247.CrossRefGoogle Scholar
Brocklehurst, A. & Pike, A.C. 1994 Reduction of BVI noise using a vane tip. In AHS Aeromechanics Specialists Conference. American Helicopter Society.Google Scholar
Brown, K., Houck, D., Maniaci, D., Westergaard, C. & Kelley, C. 2022 Accelerated wind-turbine wake recovery through actuation of the tip-vortex instability. AIAA J. 60 (5), 1–13.Google Scholar
Brynjell-Rahkola, M. & Henningson, D.S. 2020 Numerical realization of helical vortices: application to vortex instability. Theor. Comput. Fluid Dyn. 34 (1), 1–20.CrossRefGoogle Scholar
Cañadillas, B., et al. 2020 Offshore wind farm wake recovery: airborne measurements and its representation in engineering models. Wind Energy 23 (5), 1249–1265.CrossRefGoogle Scholar
Castillo-Castellanos, A., Le Dizès, S. & Durán Venegas, E. 2021 Closely spaced corotating helical vortices: general solutions. Phys. Rev. Fluids 6, 114701.CrossRefGoogle Scholar
Crouch, J.D. 1997 Instability and transient growth for two trailing-vortex pairs. J. Fluid Mech. 350, 311–330.CrossRefGoogle Scholar
Crow, S.C. 1970 Stability theory for a pair of trailing vortices. AIAA J. 8 (12), 2172–2179.CrossRefGoogle Scholar
Durán Venegas, E. & Le Dizès, S. 2019 Generalized helical vortex pairs. J. Fluid Mech. 865, 523–545.CrossRefGoogle Scholar
Durán Venegas, E., Rieu, P. & Le Dizès, S. 2021 Structure and stability of Joukowski's rotor wake model. J. Fluid Mech. 911, A6.CrossRefGoogle Scholar
Fabre, D. & Jacquin, L. 2000 Stability of a four-vortex aircraft wake model. Phys. Fluids 12 (10), 2438–2443.CrossRefGoogle Scholar
Fabre, D., Jacquin, L. & Loof, A. 2002 Optimal perturbations in a four-vortex aircraft wake in counter-rotating configuration. J. Fluid Mech. 451, 319–328.CrossRefGoogle Scholar
Frederik, J.A., Doekemeijer, B.M., Mulders, S.P. & van Wingerden, J. -W. 2020 The helix approach: using dynamic individual pitch control to enhance wake mixing in wind farms. Wind Energy 23 (8), 1739–1751.CrossRefGoogle Scholar
Fukumoto, Y. & Miyazaki, T. 1991 Three–dimensional distorsions of a vortex filament zith axial velocity. J. Fluid Mech. 222, 369–416.CrossRefGoogle Scholar
Gupta, B.P. & Loewy, R.G. 1974 Theoretical analysis of the aerodynamic stability of multiple, interdigitated helical vortices. AIAA J. 12 (10), 1381–1387.CrossRefGoogle Scholar
Hardin, J.C. 1982 The velocity field induced by a helical vortex filament. Phys. Fluids 25 (11), 1949–1952.CrossRefGoogle Scholar
Huang, X., Moghadam, S.M.A., Meysonnat, P.S., Meinke, M. & Schröder, W. 2019 Numerical analysis of the effect of flaps on the tip vortex of a wind turbine blade. Intl J. Heat Fluid Flow 77, 336–351.CrossRefGoogle Scholar
Huerre, P. & Monkewitz, P.A. 1990 Local and global instabilities in spatially developing flows. Annu. Rev. Fluid Mech. 22 (1), 473–537.CrossRefGoogle Scholar
Ivanell, S., Mikkelsen, R., Sørensen, J.N. & Henningson, D. 2010 Stability analysis of the tip vortices of a wind turbine. Wind Energy 13 (8), 705–715.CrossRefGoogle Scholar
Jimenez, J. 1975 Stability of a pair of co-rotating vortices. Phys. Fluids 18 (11), 1580–1581.CrossRefGoogle Scholar
Josserand, C. & Rossi, M. 2007 The merging of two co-rotating vortices: a numerical study. Eur. J. Mech. B/Fluids 26 (6), 779–794.CrossRefGoogle Scholar
Kawada, S. 1936 Induced velocity by helical vortices. J. Aeronaut. Sci. 3 (3), 86–87.CrossRefGoogle Scholar
Kerswell, R.R. 2002 Elliptical instability. Annu. Rev. Fluid Mech. 34 (1), 83–113.CrossRefGoogle Scholar
Kleine, V.G., Kleusberg, E., Hanifi, A. & Henningson, D.S. 2019 Tip-vortex instabilities of two in-line wind turbines. J. Phys.: Conf. Ser. 1256, 012015.Google Scholar
Lamb, H. 1945 Hydrodynamics. Dover.Google Scholar
Leishman, J.G., Bhagwat, M.J. & Bagai, A. 2002 Free-vortex filament methods for the analysis of helicopter rotor wakes. J. Aircraft 39 (5), 759–775.CrossRefGoogle Scholar
Levy, H. & Forsdyke, A.G. 1928 The steady motion and stability of a helical vortex. Proc. R. Soc. Lond. A 120, 670–690.Google Scholar
Leweke, T., Le Dizes, S. & Williamson, C.H.K. 2016 Dynamics and instabilities of vortex pairs. Annu. Rev. Fluid Mech. 48 (1), 507–541.CrossRefGoogle Scholar
Leweke, T., Quaranta, H.U., Bolnot, H., Blanco-Rodriíguez, F.J. & Le Dizès, S. 2014 Long- and short-wave instabilities in helical vortices. J. Phys.: Conf. Ser. 524, 012154.Google Scholar
Meunier, P., Ehrenstein, U., Leweke, T. & Rossi, M. 2002 A merging criterion for two-dimensional co-rotating vortices. Phys. Fluids 14 (8), 2757–2766.CrossRefGoogle Scholar
Meunier, P. & Leweke, T. 2005 Elliptic instability of a co-rotating vortex pair. J. Fluid Mech. 533, 125–159.CrossRefGoogle Scholar
Okulov, V.L. 2004 On the stability of multiple helical vortices. J. Fluid Mech. 521, 319–342.CrossRefGoogle Scholar
Okulov, V.L. & Sørensen, J.N. 2007 Stability of helical tip vortices in a rotor far wake. J. Fluid Mech. 576, 1–25.CrossRefGoogle Scholar
Okulov, V.L. & Sørensen, J.N. 2009 Applications of 2d helical vortex dynamics. Theor. Comput. Fluid Dyn. 24 (1–4), 395–401.CrossRefGoogle Scholar
Quaranta, H.U., Bolnot, H. & Leweke, T. 2015 Long-wave instability of a helical vortex. J. Fluid Mech. 780, 687–716.CrossRefGoogle Scholar
Quaranta, H.U., Brynjell-Rahkola, M., Leweke, T. & Henningson, D.S. 2019 Local and global pairing instabilities of two interlaced helical vortices. J. Fluid Mech. 863, 927–955.CrossRefGoogle Scholar
Robinson, A.C. & Saffman, P.G. 1982 Three-dimensional stability of vortex arrays. J. Fluid Mech. 125, 411–427.CrossRefGoogle Scholar
Roy, C., Schaeffer, N., Le Dizès, S. & Thompson, M. 2008 Stability of a pair of co-rotating vortices with axial flow. Phys. Fluids 20 (9), 094101.CrossRefGoogle Scholar
Schröder, D., Leweke, T., Hörnschemeyer, R. & Stumpf, E. 2020 Experimental investigation of a helical vortex pair. In Deutscher Luft-und Raumfahrtkongress 2020.Google Scholar
Schröder, D., Leweke, T., Hörnschemeyer, R. & Stumpf, E. 2021 Instability and merging of a helical vortex pair in the wake of a rotor. J. Phys.: Conf. Ser. 1934 (1), 012007.Google Scholar
Selçuk, C., Delbende, I. & Rossi, M. 2017 Helical vortices: quasiequilibrium states and their time evolution. Phys. Rev. Fluids 2 (8), 084701.CrossRefGoogle Scholar
Walther, J.H., Guénot, M., Machefaux, E., Rasmussen, J.T., Chatelain, P., Okulov, V.L., Sørensen, J.N., Bergdorf, M. & Koumoutsakos, P. 2007 A numerical study of the stabilitiy of helical vortices using vortex methods. J. Phys.: Conf. Ser. 75, 012034.Google Scholar
Widnall, S.E. 1972 The stability of a helical vortex filament. J. Fluid Mech. 54 (4), 641–663.CrossRefGoogle Scholar