Hostname: page-component-cd9895bd7-gxg78 Total loading time: 0 Render date: 2024-12-20T21:46:36.968Z Has data issue: false hasContentIssue false
  • English
  • Français

On the dynamics of three-dimensional slung prisms under very low and high turbulence flows

Published online by Cambridge University Press:  07 March 2017

Y. Jin  and
L. P. Chamorro Open the ORCID record for L. P. Chamorro [Opens in a new window]
Y. Jin
Affiliation:
Mechanical Science and Engineering Department, University of Illinois, Urbana, IL 61801, USA
L. P. Chamorro*
Affiliation:
Mechanical Science and Engineering Department, University of Illinois, Urbana, IL 61801, USA Civil and Environmental Engineering Department, University of Illinois, Urbana, IL 61801, USA Aerospace Engineering, University of Illinois, Urbana, IL 61801, USA
*
†Email address for correspondence: lpchamo@illinois.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

The distinctive pendulum-like oscillation and pitching patterns of cubic and rectangular slung prisms were inspected for two aspect ratios at various Reynolds numbers 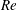$Re$ under two free-stream turbulence levels. Systematic experiments were performed using high-resolution telemetry and hotwire anemometry to quantitatively characterize the dynamics of the prisms and the wake fluctuation. The results show that the dynamics of the prisms can be characterized by two distinctive regions depending on the prism shape. Specifically, in the case of cubic prisms the regions are defined by the growth rate of the pitching amplitude; whereas the dynamics of the rectangular prisms is more sensitive to the angle of attack. In particular, when the large side initially faces the flow, the regions are defined by the synchronization between the vortex shedding and pure oscillations under very low turbulence. When the smaller side initially faces the flow, the regions are defined by the equilibrium pitching position. Regardless of the geometry of the prism and flow condition the dominant oscillation frequency resulted as being close to the natural frequency of the small-amplitude pendulum-like oscillation.

JFM classification

Aerodynamics: Aerodynamics
Type
Papers
Information
Journal of Fluid Mechanics , Volume 816 , 10 April 2017 , pp. 468 - 480
Check for updates
Copyright
© 2017 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Adrian, R. J., Meinhart, C. D. & Tomkins, C. D. 2000 Vortex organization in the outer region of the turbulent boundary layer. J. Fluid Mech. 422, 1–54.Google Scholar
Baik, Y. S., Bernal, L. P., Granlund, K. & Ol, M. V. 2012 Unsteady force generation and vortex dynamics of pitching and plunging aerofoils. J. Fluid Mech. 709, 37–68.Google Scholar
Cicolani, L., Ivler, C., Ott, C., Raz, R. & Rosen, A. 2015 Rotational stabilization of cargo container slung loads. J. Am. Helicopter Soc. 60 (4), 1–13.Google Scholar
Fail, R., Lawford, J. A. & Eyre, R. C. W. 1959 Low-speed experiments on the wake characteristics of flat plates normal to an airstream. Aero. Res. Counc. R&M 3120.Google Scholar
Flemming, F. & Williamson, C. H. K. 2005 Vortex-induced vibrations of a pivoted cylinder. J. Fluid Mech. 522, 215–252.Google Scholar
Govardhan, R. & Williamson, C. H. K. 2000 Modes of vortex formation and frequency response of a freely vibrating cylinder. J. Fluid Mech. 420, 85–130.CrossRefGoogle Scholar
Greenwell, D. I. 2014 Geometry effects on autorotation of rectangular prisms. J. Wind Engng Ind. Aerodyn. 132, 92–100.Google Scholar
Hobeck, J. D. & Inman, D. J. 2014 A distributed parameter electromechanical and statistical model for energy harvesting from turbulence-induced vibration. Smart Mater Struct. 23 (11), 115003.Google Scholar
Irwin, P. A. 2008 Bluff body aerodynamics in wind engineering. J. Wind Engng Ind. Aerodyn. 96 (6), 701–712.Google Scholar
Jantzen, R. T., Taira, K., Granlund, K. O. & Ol, M. V. 2014 Vortex dynamics around pitching plates. Phys. Fluids 26 (5), 053606.CrossRefGoogle Scholar
Jin, Y., Ji, S. & Chamorro, L. P. 2016a Spectral energy cascade of body rotations and oscillations under turbulence. Phys. Rev. E 94, 063105.Google Scholar
Jin, Y., Ji, S., Liu, B. & Chamorro, L. P. 2016b On the role of thickness ratio and location of axis of rotation in the flat plate motions. J. Fluids Struct. 64, 127–137.Google Scholar
Jin, Y., Liu, H., Aggarwal, R., Singh, A. & Chamorro, L. P. 2016c Effects of freestream turbulence in a model wind turbine wake. Energies 9 (10), 830; doi:10.3390/en9100830.Google Scholar
Khalak, A. & Williamson, C. H. K. 1999 Motions, forces and mode transitions in vortex-induced vibrations at low mass-damping. J. Fluids Struct. 13 (7), 813–851.Google Scholar
Knisely, C. W. 1990 Strouhal numbers of rectangular cylinders at incidence: a review and new data. J. Fluids Struct. 4 (4), 371–393.Google Scholar
Mittal, S. 2016 Lock-in in vortex-induced vibration. J. Fluid Mech. 794, 565–594.Google Scholar
Nakamura, Y. & Ohya, Y. 1984 The effects of turbulence on the mean flow past two-dimensional rectangular cylinders. J. Fluid Mech. 149, 255–273.Google Scholar
Nemes, A., Zhao, J., Jacono, D. L. & Sheridan, J. 2012 The interaction between flow-induced vibration mechanisms of a square cylinder with varying angles of attack. J. Fluid Mech. 710, 102–130.Google Scholar
Onoue, K., Song, A., Strom, B. & Breuer, K. S. 2015 Large amplitude flow-induced oscillations and energy harvesting using a cyber-physical pitching plate. J. Fluids Struct. 55, 262–275.Google Scholar
Prosser, D. T. & Smith, M. J. 2015 A physics-based, reduced-order aerodynamics model for bluff bodies in unsteady, arbitrary motion. J. Am. Helicopter Soc. 60 (3), 1–15.Google Scholar
Prosser, D. T. & Smith, M. J. 2016 Numerical characterization of three-dimensional bluff body shear layer behaviour. J. Fluid Mech. 799, 1–26.CrossRefGoogle Scholar
Raz, R., Rosen, A., Carmeli, A., Lusardi, J., Cicolani, L. S. & Robinson, D. 2008 Wind tunnel and flight evaluation of stability and passive stabilization of cargo container slung load. In American Helicopter Society 64th Annual Forum, Montreal, Canada, AHS International.Google Scholar
Raz, R., Rosen, A., Cicolani, L. S. & Lusardi, J. 2014 Using wind tunnel tests for slung-load clearance, part 1: the conex cargo container. J. Am. Helicopter Soc. 59 (4), 1–12.Google Scholar
Rosen, A., Cecutta, S. & Yaffe, R. 1999 Wind tunnel tests of cube and conex models. In Technion Institute of Technology, Dept. of Aerospace Engineering, TAE, vol. 844.Google Scholar
Sarpkaya, T. 2004 A critical review of the intrinsic nature of vortex-induced vibrations. J. Fluids Struct. 19 (4), 389–447.CrossRefGoogle Scholar
Sen, S. & Mittal, S. 2011 Free vibration of a square cylinder at low Reynolds numbers. J. Fluids Struct. 27 (5), 875–884.Google Scholar
Smith, E. H. 1971 Autorotating wings: an experimental investigation. J. Fluid Mech. 50 (3), 513–534.Google Scholar
Tamura, T. & Miyagi, T. 1999 The effect of turbulence on aerodynamic forces on a square cylinder with various corner shapes. J. Wind Engng Ind. Aerodyn. 83 (1), 135–145.Google Scholar
Tatsuno, M., Takayama, T., Amamoto, H. & Ishi-i, K. 1990 On the stable posture of a triangular or a square cylinder about its central axis in a uniform flow. Fluid Dyn. Res. 6, 201–207.Google Scholar
Theodorsen, T.1935 General theory of aerodynamic instability and the mechanism of flutter, NASA Tech. Rep. 496.Google Scholar
Von Kármán, T. 1938 Airfoil theory for non-uniform motion. J. Aero. Sci. 5 (10), 379–390.Google Scholar
Williamson, C. H. K. & Govardhan, R. 2004 Vortex-induced vibrations. Annu. Rev. Fluid Mech. 36 (1), 413–455.Google Scholar
Wu, X., Ge, F. & Hong, Y. 2012 A review of recent studies on vortex-induced vibrations of long slender cylinders. J. Fluids Struct. 28, 292–308.Google Scholar
Zaki, T. G. & Gad-El-Hak, M. 1994 Numerical and experimental investigation of flow past a freely rotatable square cylinder. J. Fluids Struct. 8 (7), 555–582.CrossRefGoogle Scholar
Zhao, J., Leontini, J. S, Jacono, D. L. & Sheridan, J. 2014 Fluid–structure interaction of a square cylinder at different angles of attack. J. Fluid Mech. 747, 688–721.Google Scholar
Zhao, M. 2015 Flow-induced vibrations of square and rectangular cylinders at low Reynolds number. Fluid Dyn. Res. 47 (2), 025502.Google Scholar