Alahyari, A. & Longmire, E. K.
1994
Particle image velocimetry in a variable density flow: application to a dynamically evolving microburst. Exp. Fluids
17, 434–440.
Alavian, V.
1986
Behavior of density currents on an incline. ASCE J. Hydraul. Engng
112, 27–42.
Atsavapranee, P. & Gharib, M.
1997
Structures in stratified plane mixing layers and the effects of cross-shear. J. Fluid Mech.
342, 53–86.
Bacon, S.
1998
Decadal variablity in the outflow from the Nordic seas to the deep Atlantic Ocean. Nature
394, 871–874.
Baines, P. G.
2001
Mixing in flows down gentle slopes into stratified environment. J. Fluid Mech.
443, 237–270.
Baines, P. G.
2002
Two-dimensional plumes in stratified environments. J. Fluid Mech.
471, 315–337.
Baines, P. G.
2005
Mixing regimes for the flow of dense fluid down slopes into stratified environment. J. Fluid Mech.
538, 245–267.
Barry, M. E., Ivey, G. N., Winters, K. B. & Imberger, J.
2001
Measurements of diapycnal diffusivities in stratified fluids. J. Fluid Mech.
442, 267–291.
Bluteau, C. E., Jones, N. L. & Ivey, G. N.
2013
Turbulent mixing efficiency at an energetic ocean site. J. Geophys. Res.-Oceans
118, 4662–4672.
Borg, A., Bolinder, J. & Fuchs, L.
2001
Simultaneous velocity and concentration measurements in the near field of a turbulent low-pressure jet by digital particle image velocimetry – planar laser-induced fluorescence. Exp. Fluids
31, 140–152.
Bouffard, D. & Boegman, L.
2013
A diapycnal diffusivity model for stratified environmental flows. Dyn. Atmos. Oceans
61–62, 14–34.
Broecker, W. S.
1997
Thermohaline circulation, the Achilles heel of our climate system: will man-made
$\mathrm{CO}_{2}$
upset the current balance?. Science
278 (5343), 1582–1588.
Cenedese, C. & Adduce, C.
2008
Mixing in a density-driven current flowing down a slope in a rotating fluid. J. Fluid Mech.
604, 369–388.
Cenedese, C. & Adduce, C.
2010
A new parameterization for entrainment in overflows. J. Phys. Oceanogr.
40 (8), 1835–1850.
Cenedese, C., Whitehead, J. A., Ascarelli, T. A. & Ohiwa, M.
2004
A dense current flowing down a sloping bottom in a rotating fluid. J. Phys. Oceanogr.
34, 188–203.
Chen, J., Meneveau, C. & Katz, J.
2006
Scale interactions of turbulence subjected to a straining–relaxation–destraining cycle. J. Fluid Mech.
562, 123–150.
Crimaldi, J. P.
1997
The effect of photobleaching and velocity fluctuations on single-point LIF measurements. Exp. Fluids
23 (4), 325–330.
Crimaldi, J. P.
2008
Planar laser induced fluorescence in aqueous flows. Exp. Fluids
44 (6), 851–863.
Daviero, G. J., Roberts, P. J. W. & Maile, K.
2001
Refractive index matching in large-scale stratified experiments. Exp. Fluids
31, 119–126.
Doron, P., Bertuccioli, L., Katz, J. & Osborn, T.
2001
Turbulence characteristics and dissipation estimates in the costal ocean bottom boundary layer from PIV data. J. Phys. Oceanogr.
31, 2108–2134.
Du, H., Fuh, R. A., Li, J., Corkan, A. & Lindsey, J. S.
1998
PhotochemCAD: a computer-aided design and research tool in photochemistry. Photochem. Photobiol.
68, 141–142.
Ellison, T. H.
1957
Turbulent transport of heat and momentum from an infinite rough plane. J. Fluid Mech.
2 (5), 456–466.
Ellison, T. H. & Turner, J. S.
1959
Turbulent entrainment in stratified flows. J. Fluid Mech.
6, 423–448.
Feng, H., Olsen, M. G., Hill, J. C. & Fox, R. O.
2007
Simultaneous velocity and concentration filed measurements of passive-scalar mixing in a confined rectangular jet. Exp. Fluids
42, 847–862.
Ferrier, A. J., Funk, D. R. & Roberts, P. J. W
1993
Application of optical techniques to the study of plumes in stratified fluids. Dyn. Atmos. Oceans
20, 155–183.
Girton, J. & Sanford, T.
2003
Desent and modification of the overflow plume in the Denmark Strait. J. Phys. Oceanogr.
33, 1351–1364.
Girton, J., Sanford, T. & Kase, R.
2001
Synoptic sections of the Denmark Strait overflow. Geophys. Res. Lett.
28, 1619–1622.
Hallworth, M. A., Phillips, J. C., Huppert, H. E., Stephen, R. & Sparks, J.
1993
Entrainment in turbulent gravity currents. Nature
362, 829–831.
Hannoun, I. A., Fernando, H. J. S. & List, E. J.
1988
Turbulent structure near a sharp density interface. J. Fluid Mech.
189, 189–209.
Hansen, B. & Østerhus, S.
2000
North Atlantic–Nordic seas exchange. Prog. Oceanogr.
45, 109–208.
Hjertager, L. K., Hjertager, B. H., Deen, N. G. & Solberg, T.
2003
Measurement of turbulent mixing in a confined wake flow using combined PIV and PLIF. Can. J. Chem. Engng
81, 1149–1158.
Hu, H., Kobayashi, T., Segawa, S. & Taniguchi, N.
2000
Particle image velocimetry and planar laser-induced fluorescence measurements on lobed jet mixing flows. Exp. Fluids (Suppl.), S141–S157.
Huang, H., Diabiri, D. & Gharib, M.
1997
On the error of digital particle image velocimetry. Meas. Sci. Technol.
8, 1427–1440.
Hult, E. L., Troy, C. D. & Koseff, J. R.
2011
The mixing efficiency of interfacial waves breaking at a ridge: 2. Local mixing processes. J. Geophys. Res.-Oceans
116, C02004.
Huppert, H. E.
2006
Gravity currents: a personal perspective. J. Fluid Mech.
554, 299–322.
Ilicak, M., Özgökmen, T. M., Baumert, H. Z. & Iskandarani, M.
2008
Performance of two-equation turbulence closures in three-dimensional simulations of the red sea overflow. Ocean Model.
24, 122–139.
Istweire, E. C., Koseff, J. R., Briggs, D. A. & Ferziger, J. H.
1993
Turbulence in stratified shear flows – implications for interpreting shear-induced mixing in the ocean. J. Fluid Mech.
23 (7), 1508–1522.
Ivey, G. N., Winters, K. B. & Koseff, J. R.
2008
Density stratification, turbulence, but how much mixing?. Annu. Rev. Fluid Mech.
40, 169–184.
Jackson, L., Hullberg, R. & Legg, S.
2008
A parameterization of shear-driven turbulence for ocean climate models. J. Phys. Oceanogr.
38, 1033–1053.
Kang, H., Stuart, C. & Meneveau, C.
2003
Decaying turbulence in an active-grid-generated flow and comparisions with large-eddy-simulation. J. Fluid Mech.
480, 129–160.
Karasso, P. S. & Mungal, M. G.
1997
Plif measurements in aqueous flows using the Nd:YAG laser. Exp. Fluids
27, 82–87.
Keane, R. & Adrian, R.
1990
Optimization of particle image velocimeters, part I, double pulsed systems. Meas. Sci. Technol.
1, 1202–1215.
Knauss, J. A.
1978
Introduction to Physical Oceanography. Prentice-Hall Inc.
Kneller, B. C., Bennett, S. J. & McCaffrey, W. D.
1999
Velocity structure, turbulence and fluid stresses in experimental gravity current. J. Geophys. Res.
104, 5381–5391.
Koop, C. G. & Browand, F. K.
1979
Instability and turbulence in a stratified fluid with shear. J. Fluid Mech.
93 (01), 135–159.
Krug, D., Holzner, M., Luethi, B., Wolf, M., Kinzelbach, W. & Tsinober, A.
2013
Experimental study of entrainment and interface dynamics in a gravity current. Exp. Fluids
54 (5), 1530.
Lane-Serff, G. F. & Baines, P. G.
1998
Eddy formation by dense flows on slopes in a rotating fluid. J. Fluid Mech.
363, 229–252.
Launder, B. E. & Rodi, W.
1983
The turbulent wall jet – measurements and modeling. Annu. Rev. Fluid Mech.
15, 429–459.
Legg, S., Hallberg, R. W. & Girton, J. B.
2006
Comparison of entrainment in overflows simulated by
$z$
-coordinate, isopycnal and non-hydrostatic models. Ocean Model.
11, 69–97.
Linden, P. F.
1979
Mixing in stratified fluids. Geophys. Astrophys. Fluid Dyn.
13, 2–23.
Lowe, R. J., Linden, P. F. & Rottman, J. W.
2002
A laboratory study of the velocity structure in an intrusive gravity current. J. Fluid Mech.
456, 33–48.
Makita, H.
1991
Realization of a large-scale turbulence field in a small wind tunnel. Fluid Dyn. Res.
8, 53–64.
McDougall, T. J.
1979
On the elimination of refractive-index variations in turbulent density-stratified liquid flows. J. Fluid Mech.
93, 83–96.
Mellor, G. L. & Yamada, T.
1974
A hierarchy of turbulence closure models for planetary boundary layers. J. Atmos. Sci.
31, 1791–1806.
Mellor, G. L. & Yamada, T.
1982
Development of a turbulence closure model for geophysical fluid problems. Rev. Geophys. Space Phys.
20, 851–875.
Monin, A. & Yaglom, A.
1971
Statistical Fluid Mechanics. MIT Press.
Morton, B. R., Taylor, G. I. & Turner, J. S.
1956
Turbulent gravitational convection from maintained and instantaneous sources. Proc. R. Soc. Lond.
A234, 1–23.
Mydlarski, L. & Warhaft, Z.
1996
On the onset of high-Reynolds-number grid-generated wind tunnel turbulence. J. Fluid Mech.
320, 331–368.
Odier, P., Chen, J. & Ecke, R. E.
2012
Understanding and modeling turbulent fluxes and entrainment in a gravity current. Physica D
241 (3, SI), 260–268.
Odier, P., Chen, J., Rivera, M. & Ecke, R.
2009
Fluid mixing in stratified gravity currents: the Prandtl mixing length. Phys. Rev. Lett.
102, 134504.
Osborn, T. R.
1980
Estimates of the local-rate of vertical diffusion from dissipation measurements. J. Phys. Oceanogr.
10 (1), 83–89.
Özgökmen, T. M., Fischer, P. F., Duan, J. & Iliescu, T.
2004
Three-dimensional turbulent bottom density currents from a high-order nonhydrostatic spectral element model. J. Phys. Oceanogr.
34, 2006–2026.
Pardyjak, E. R., Monti, P. & Fernando, H. J. S.
2002
Flux richardson number measurements in stable atmosphere shear flows. J. Fluid Mech.
459, 307–316.
Peltier, W. & Caulfield, C.
2003
Mixing efficiency in stratified shear flows. Annu. Rev. Fluid Mech.
35, 135–167.
Pope, S.
2000
Turbulent Flows. Cambridge University Press.
Price, J., Baringer, M., Lueck, R., Johnson, G., Ambar, I., Parrilla, G., Cantos, A., Kennelly, M. A. & Sanford, T. B.
1993
Mediterranean outflow mixing and dynamics. Science
259, 1278–1282.
Princevac, M., Fernando, H. J. S. & Whiteman, C. D.
2005
Turbulent entrainment into natural gravity-driven flows. J. Fluid Mech.
533, 259–268.
Raffel, M., Willert, C. & Kompenhans, J.
1998
Particle Image Velocimetry – A Practical Guide. Springer.
Raffel, M., Willert, C. E., Wereley, S. T. & Kompenhans, J.
2007
Particle Image Velocimetry – A Practical Guide. 2nd edn. Springer.
Rohr, J. J., Itsweire, E. C., Helland, K. N. & Van Atta, C. W.
1988
Growth and decay of turbulence in a stably stratified shear-flow. J. Fluid Mech.
195, 77–111.
Roth, G. & Katz, J.
2001
Five techniques for increasing the speed and accuracy of PIV interrogaton. Meas. Sci. Technol.
12, 238–245.
Schwarz, W. H. & Cosart, W. P.
1961
The two-dimensional turbulent wall-jet. J. Fluid Mech.
10, 481–495.
Shapiro, G. I. & Zatsepin, A. G.
1997
Gravity current down a steeply inclined slope in a rotating fluid. Ann. Geophys.
15, 366–374.
Shih, L. H., Koseff, J. R., Ivey, G. N. & Ferziger, J. H.
2005
Parameterization of turbulent fluxes and scales using homogeneous sheared stably stratified turbulence simulations. J. Fluid Mech.
525, 193–214.
Simpson, J. E.
1982
Gravity currents in the laboratory, atmosphere, and ocean. Annu. Rev. Fluid Mech.
14, 213–234.
Simpson, J.
1987
Gravity Currents: In the Environment and the Laboratory. Ellis Horwood Ltd.
Stillinger, D. C., Helland, K. N. & Atta, C. W. Van
1983
Experiments on the transition of homogeneous turbulence to internal waves in a stratified fluid. J. Fluid Mech.
131, 91.
Strang, E. J. & Fernando, H. J. S.
2001a
Entrainment and mixing in stratified shear flows. J. Fluid Mech.
428, 349–386.
Strang, E. J. & Fernando, H. J. S.
2001b
Vertical mixing and transports through a stratified shear layer. J. Phys. Oceanogr.
31, 2026–2048.
Strang, E. J. & Fernando, H. J. S.
2004
Shear-induced mixing and transport from a rectangular cavity. J. Fluid Mech.
520, 23–49.
Sutherland, B. R.
2002
Interfacial gravity currents. I. Mixing and entrainment. Exp. Fluids
14, 2244–2254.
Tanaka, T. & Eaton, J. K.
2007
A correction method for measuring turbulence kinetic energy dissipation rate by PIV. Exp. Fluids.
Tennekes, H. & Lumley, J.
1972
A First Course in Turbulence. MIT Press.
Thomas, P. J. & Linden, P. F.
2007
Rotating gravity currents: small-scale and large-scale laboratory experiments and geostrophic model. J. Fluid Mech.
578, 35–65.
Townsend, A. A.
1958
The effects of radiative transfer on turbulent flow of a stratified fluid. J. Fluid Mech.
361–372.
Troy, C. & Koseff, J.
2005
The generation and quantitative visualization of breaking internal waves. Exp. Fluids
38, 549–562.
Turner, J. S.
1973
Buoyancy Effects in Fluids. Cambridge University Press.
Turner, J. S.
1986
Turbulent entrainment: the development of the entrainment assumption, and its application to geophysical flows. J. Fluid Mech.
173, 431–471.
Wells, M., Cenedese, C. & Caulfield, C. P.
2010
The relationship between flux coefficient and entrainment ratio in density currents. J. Phys. Oceanogr.
40 (12), 2713–2727.
Willebrand, J., Barnier, B., Böning, C., Dieterich, C., Killworth, P. D., Le Provost, C., Jia, Y., Molines, J. -M. & New, A. L.
2001
Circulation characteristics in three eddy-permitting models of the North Atlantic. Prog. Oceanogr.
48, 123–161.
Wunsch, C. & Ferrari, R.
2004
Vertical mixing, energy and thegeneral circulation of the oceans. Annu. Rev. Fluid Mech.
36, 281–314.
Wygnanski, I., Katz, Y. & Horev, E.
1992
On the applicability of various scaling laws to the turbulent wall jet. J. Fluid Mech.
234, 669–690.
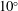$10^\circ $
with respect to horizontal. The turbulence level of the input flow is controlled by injecting velocity fluctuations upstream of the output nozzle. The initial Reynolds number based on the Taylor microscale of the flow,
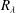$R_{\lambda }$
, is varied between 40 and 120, and the effects of the initial turbulence level are assessed. The bulk Richardson number
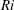$\mathit{Ri}$
for the flow is
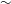${\sim }$
0.3 whereas the gradient Richardson number
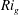$\mathit{Ri}_g$
varies between 0.04 and 0.25, indicating that shear dominates the stabilizing effect of stratification. Kelvin–Helmholtz instability results in vigorous vertical transport of mass and momentum. We present baseline characterization of standard turbulence quantities and calculate, in several different ways, the fluid entrainment coefficient
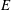$E$
, a quantity of considerable interest in mixing parameterization for ocean circulation models. We also determine the properties of mixing as represented by the flux Richardson number
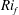$\mathit{Ri}_f$
as a function of
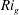$\mathit{Ri}_g$
and diapycnal mixing parameter
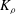$K_{\rho }$
versus the buoyancy Reynolds number
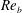$\mathit{Re}_b$
. We find reasonable agreement with results from natural flows.
